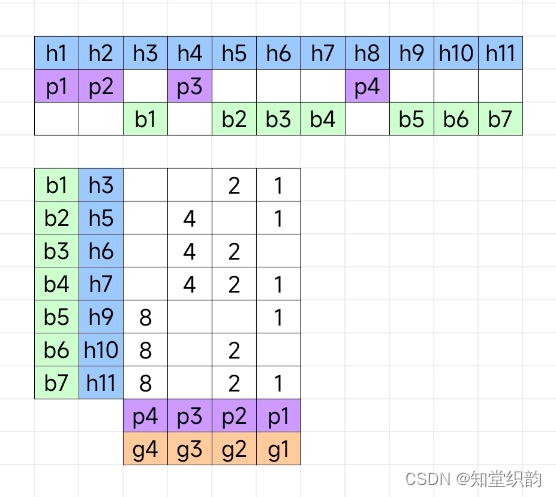
在上图中,对绿色的7比特数据进行海明校验,需要添加紫色的4比特校验位,总共是蓝色的11比特。紫色的校验位pi分布于蓝色的hi的1, 2, 4, 8, 16, 32, 64位,是2i-1位。绿色的数据位bi分布于剩下的位。
在下图中,b1位于h3,3=2+1
b2位于h5,5=4+1
......
b7位于h11,11=8+2+1
然后竖着看,p4上边有3个8,分别对应b5, b6, b7,p4的值等于这三位的偶校验的结果。
......
p1上边有5个1,p1的值等于对b1, b2, b4, b5, b7的偶校验的结果。
算出p4p3p2p1后,按上图的位置代入hi,校验完成。
然后,接收方拿到hi,计算gi,计算方法看下图。g4上边有3个8和1个p4,3个8对应b5, b6, b7,g4的值等于对b5, b6, b7, p4求偶校验的结果。
......
计算了g4g3g2g1后,发现它的值等于0000,这表示没有错误。若值为1001,即十进制的9,这表明h9出错。
以上是不出错,或只有1比特出错的情况。实际上,当同时有多个比特出错时,即使G=0000,也不能保证不出错;G=1001,不能保证一定是h9出错了。
实践中,用11比特hi,再加上1比特偶校验位,来增强校验效果。