
TensorFlow 是一个开源的软件库,用于数值计算,特别适用于大规模的机器学习。它由 Google 的研究人员和工程师在 Google Brain 团队内部开发,并在 2015 年首次发布。TensorFlow 的核心是使用数据流图来组织计算,使得它可以轻松地利用多种不同的硬件平台,从普通的个人电脑到大型服务器,甚至包括移动设备和边缘设备。
1.Tensorflow的特点和使用场景
主要特点
1.灵活性和可扩展性:TensorFlow 支持多种不同的模型和算法,用户也可以定义自己的操作,使其适应几乎任何任务的计算需求。它可以运行在多种设备上,包括桌面、服务器、移动设备等。
2.自动微分:TensorFlow 提供自动微分功能,意味着系统可以自动帮你计算导数,这一点对于实现机器学习算法中的反向传播等技术尤为重要。
3.性能优化:TensorFlow 提供了多种工具和库,支持对计算图进行优化,能够自动使用 CPU 和 GPU 等硬件加速功能。
4.易于部署:TensorFlow 模型可以轻松地部署到多种平台,用户不需要在不同设备上重新编写代码。
5.大规模机器学习支持:TensorFlow 特别适用于从中到大规模的机器学习项目。
6.生态系统和社区:TensorFlow 拥有广泛的生态系统,包括各种工具、库和社区资源,可以帮助用户从数据准备到模型训练再到部署都得到支持。
使用场景
-
图像和视频处理:如图像识别、物体检测和视频分析。
-
自然语言处理:如语言翻译、情感分析和文本分类。
-
声音识别:如语音到文本的转换。
-
预测分析:如股票市场预测、能源需求预测等。
-
强化学习:如游戏和机器人控制系统的开发。
TensorFlow 也不断在发展,增加新功能和改进,例如 TensorFlow 2.x 版本对初学者更友好,简化了很多操作,强化了即时执行(eager execution)的特性,使得交互式开发更为直观和方便。
2.Tensorflow入门
创建一个TensorFlow常量并打印:
import tensorflow as tf
# 创建一个TensorFlow常量
hello = tf.constant('Hello TensorFlow')
# 使用 TensorFlow 2.x 的方式打印这个常量
print(hello.numpy()) # 转换为NumPy数组格式并打印出来,输出结果中字母b前缀表示该字符串是一个字节串(bytes)而不是一个普通的字符串(str)
# 输出:
'''
b'Hello TensorFlow'
'''创建一个TensorFlow常量并打印:
import tensorflow as tf
# 创建两个TensorFlow常量
a = tf.constant(40)
b = tf.constant(2)
# 直接执行加法操作并打印结果
result = a + b
print(result.numpy())
# 输出:
'''
42
'''实现一个简单的线性回归模型:
线性回归模型是统计学中用来预测连续变量关系的一种方法。它假设两个或多个变量之间存在线性关系,即一个变量可以被其他一个或多个变量的线性组合来预测。线性回归的目的是找到这些变量之间最佳的直线(或超平面,取决于变量的数量)关系。
想象一下你有一组数据点,这些点在二维空间中分布(即每个数据点都有一个 x 值和一个 y 值)。线性回归模型会尝试画一条直线穿过这些点,使得所有数据点到这条直线的垂直距离之和(称为误差或残差)最小。这条直线就是所谓的"最佳拟合直线"。
在数学上,线性回归可以表示为:
其中:
-
( y ) 是因变量(目标预测值)
-
( x ) 是自变量(输入特征)
-
( w ) 是权重或系数(决定了线的斜率)
-
( b ) 是偏置或截距(决定了线的位置)
假设你想预测房屋的销售价格。这里,销售价格(( y ))可以被房屋的大小(( x ))来预测。通过收集一些历史数据(已知的房屋大小和对应的售价),你可以使用线性回归模型来找出大小和价格之间的关系。得到的模型可能会告诉你,每增加一个单位的房屋大小,价格会增加多少。
尽管线性回归是一个强大的工具,但它假设输入和输出之间是线性关系,这在现实世界中并不总是成立。当存在非线性关系时,可能需要考虑更复杂的模型,如多项式回归或其他类型的机器学习模型。
下面是一个简单的线性回归模型,用来学习并预测数据点的线性关系。
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
# 使用numpy随机生成100个数据
x_data = np.float32(np.random.rand(2, 100)) # 一个2x100的矩阵,生成了100个具有两个特征的数据点
y_data = np.dot([0.100, 0.200], x_data) + 0.300 # 是目标输出,计算公式为y_data=0.1×x1+0.2×x2+0.3
# 构造一个线性模型
b = tf.Variable(tf.zeros([1])) # 一个初始值为0的标量
w = tf.Variable(tf.random.uniform([1, 2], -1.0, 1.0)) # 权重,一个1x2的矩阵,初始化为在 [-1.0, 1.0] 范围内的随机值
x_data_tensor = tf.constant(x_data)
# 定义模型和损失函数
def model():
return tf.matmul(w, x_data_tensor) + b # 计算的是y=wx+b,使用tf.matmul来进行矩阵乘法(w 和 x_data)
def loss(): # 计算模型输出与真实输出之间的均方误差
return tf.reduce_mean(tf.square(model() - y_data))
# 最小化方差
optimizer = tf.optimizers.SGD(0.5) # 创建了一个梯度下降优化器,学习率为0.5
# 记录损失函数值
loss_values = []
steps = []
# 模拟训练:
for step in range(201):
with tf.GradientTape() as tape: # 自动计算损失函数关于模型参数的梯度
current_loss = loss()
gradients = tape.gradient(current_loss, [w, b])
optimizer.apply_gradients(zip(gradients, [w, b]))
if step % 5 == 0: # 每5步记录一次
loss_values.append(current_loss.numpy())
steps.append(step)
print(step, w.numpy(), b.numpy(), 'loss:', current_loss.numpy())
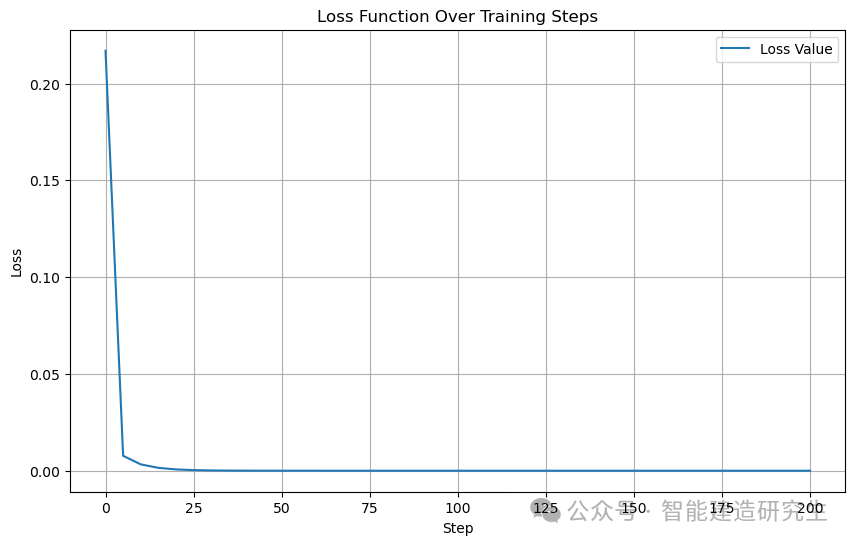
# 绘制损失函数变化图
plt.figure(figsize=(10, 6))
plt.plot(steps, loss_values, label='Loss Value')
plt.xlabel('Step')
plt.ylabel('Loss')
plt.title('Loss Function Over Training Steps')
plt.legend()
plt.grid(True)
plt.show()
# 输出:
'''
0 [[-0.10613185 0.5930704 ]] [0.44480804] loss: 0.21698055
5 [[-0.09899352 0.40378755]] [0.2845074] loss: 0.0077084834
10 [[-0.03101536 0.34016445]] [0.2949372] loss: 0.0032845887
15 [[0.01170078 0.2942564 ]] [0.29628983] loss: 0.0014881333
20 [[0.04059353 0.2634889 ]] [0.29748333] loss: 0.00067443977
···
190 [[0.09999996 0.20000012]] [0.29999995] loss: 1.7585933e-15
195 [[0.09999999 0.20000009]] [0.29999995] loss: 1.0924595e-15
200 [[0.09999999 0.20000009]] [0.29999995] loss: 1.0214052e-15
<Figure size 1000x600 with 1 Axes>
'''
使用TensorFlow2.X计算矩阵乘法:
import tensorflow as tf
# 创建一个常量op, 返回值 'matrix1' 代表这个1x2矩阵.
matrix1=tf.constant([[3.,3.]])
# 创建另外一个常量op, 返回值 'matrix2' 代表这个2x1矩阵.
matrix2 = tf.constant([[2.],[2.]])
# 创建一个矩阵乘法matmul op , 把 'matrix1' 和 'matrix2' 作为输入.
# 返回值 'product' 代表矩阵乘法的结果.
product = tf.matmul(matrix1, matrix2)
matrix1
matrix2
product # 返回的是Tensorflow对象
# 打印结果
print(product.numpy())
'''
<tf.Tensor: shape=(1, 2), dtype=float32, numpy=array([[3., 3.]], dtype=float32)>
<tf.Tensor: shape=(2, 1), dtype=float32, numpy=
array([[2.],
[2.]], dtype=float32)>
<tf.Tensor 'MatMul_8:0' shape=(1, 1) dtype=float32>
[[12.]]
'''以上内容总结自网络,如有帮助欢迎转发,我们下次再见!