leetcode77.组合 - 技术栈

给定两个整数 n 和 k，返回范围 $1, n$ 中所有可能的 k 个数的组合。

你可以按任何顺序返回答案。

解题思路

1.回溯函数终止条件

什么时候到达所谓的叶子节点了呢？

path这个数组的大小如果达到k，说明我们找到了一个子集大小为k的组合了，在图中path存的就是根节点到叶子节点的路径。

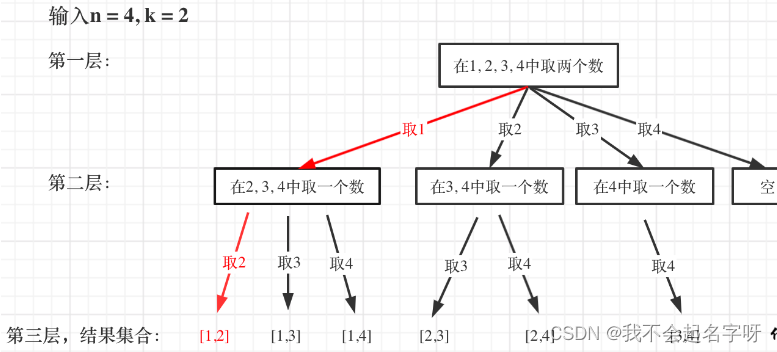
2。单层搜索的过程

回溯法的搜索过程就是一个树型结构的遍历过程，在如下图中，可以看出for循环用来横向遍历，递归的过程是纵向遍历。

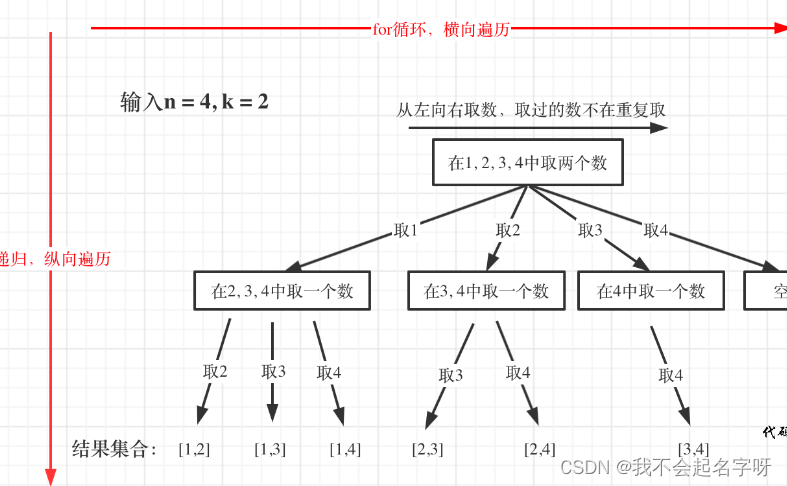
回溯法模版

c 复制代码

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

回溯法（未剪枝）

c 复制代码

int *path;
 int pathTop;
 int **ans;
 int ansTop;
 void  backTracking(int n,int k,int startIndex){
    if(pathTop==k){
        int* tmp=(int*)malloc(sizeof(int)*k);
        for(int i=0;i<k;i++){
            tmp[i]=path[i];
        }
        ans[ansTop++]=tmp;
        return;
    }
    for(int j=startIndex;j<=n;j++){
        path[pathTop++]=j;
         backTracking(n,k,j+1);
         pathTop--;
    }
 }
int** combine(int n, int k, int* returnSize, int** returnColumnSizes) {
    path=(int*)malloc(sizeof(int)*k);
    ans=(int**)malloc(sizeof(int*)*200001);
    pathTop=ansTop=0;
    backTracking(n,k,1);
    *returnSize=ansTop;//组合个数
    *returnColumnSizes=(int*)malloc(sizeof(int)*(*returnSize));//每个组合的个数
    for(int i=0;i<*returnSize;i++)
    (*returnColumnSizes)[i]=k;
    return ans;
}

回溯法（剪枝）

c 复制代码

int *path;
 int pathTop;
 int **ans;
 int ansTop;
 void  backTracking(int n,int k,int startIndex){
    if(pathTop==k){
        int* tmp=(int*)malloc(sizeof(int)*k);
        for(int i=0;i<k;i++){
            tmp[i]=path[i];
        }
        ans[ansTop++]=tmp;
        return;
    }
    for(int j=startIndex;j<=n-(k-pathTop)+1;j++){
        path[pathTop++]=j;
         backTracking(n,k,j+1);
         pathTop--;
    }
 }
int** combine(int n, int k, int* returnSize, int** returnColumnSizes) {
    path=(int*)malloc(sizeof(int)*k);
    ans=(int**)malloc(sizeof(int*)*200001);
    pathTop=ansTop=0;
    backTracking(n,k,1);
    *returnSize=ansTop;//组合个数
    *returnColumnSizes=(int*)malloc(sizeof(int)*(*returnSize));//每个组合的个数
    for(int i=0;i<*returnSize;i++)
    (*returnColumnSizes)[i]=k;
    return ans;
}