题目总结
1.给你一个整数数组 hours,表示以 小时 为单位的时间,返回一个整数,表示满足 i < j 且 hours[i] + hours[j] 构成 整天 的下标对 i, j 的数目。
整天 定义为时间持续时间是 24 小时的 整数倍。
例如,1 天是 24 小时,2 天是 48 小时,3 天是 72 小时,以此类推。
示例 1:
输入: hours = [12,12,30,24,24]
输出: 2
解释:
构成整天的下标对分别是 (0, 1) 和 (3, 4)。
class Solution {
public:
long long countCompleteDayPairs(vector<int> &hours) {
long long ans = 0;
int cnt[24]{};
for (int t : hours) {
// 先查询 cnt,再更新 cnt,因为题目要求 i<j
// 如果先更新,再查询,就把 i=j 的情况也考虑进去了
ans += cnt[(24 - t % 24) % 24];
cnt[t % 24]++;
}
return ans;
}
};
使用范围基于的for循环 (for (int t : hours)) 遍历 hours 数组中的每个元素 t。
在每次迭代中,首先计算 (24 - t % 24) % 24 来找到与当前小时数 t 相加能构成整天的那个小时数且位于当前小时数t之前(注意这里使用了两次取模运算,第一次是为了确保 t 在0到23之间,第二次是为了处理 t 本身为24的倍数的情况)。
然后,将 cnt[(24 - t % 24) % 24] 的值加到 ans 上。这里 cnt[(24 - t % 24) % 24] 表示在遍历到当前元素 t 之前,已经遍历过的小时数中与 t 相加能构成整天的那些小时数出现的次数。
最后,更新 cnt[t % 24] 的值,表示当前小时数 t 出现的次数加1。这里再次使用取模运算来确保小时数在0到23之间。
给你一个二进制数组 nums 。
你可以对数组执行以下操作 任意 次(也可以 0 次):
- 选择数组中 任意连续 3 个元素,并将它们 全部反转 。
反转 一个元素指的是将它的值从 0 变 1 ,或者从 1 变 0 。
请你返回将 nums 中所有元素变为 1 的 最少 操作次数。如果无法全部变成 1 ,返回 -1 。
示例 1:
**输入:**nums = [0,1,1,1,0,0]
**输出:**3
解释:
我们可以执行以下操作:
-
选择下标为 0 ,1 和 2 的元素并反转,得到
nums = [++1++,++0++,++0++,1,0,0]。 -
选择下标为 1 ,2 和 3 的元素并反转,得到
nums = [1,++1++,++1++,++0++,0,0]。 -
选择下标为 3 ,4 和 5 的元素并反转,得到
nums = [1,1,1,++1++,++1++,++1]++class Solution {
public:
int minOperations(vector<int>& nums) {
int n = nums.size();
int ans = 0;
for (int i = 0; i + 2 < n; i++) {
if (nums[i] == 0) {
for (int j = 0; j < 3; j++)
{
if(nums[i+j]==0)
nums[i + j] = 1;
else
nums[i+j]=0;
}
ans++;
}
}
if (nums[n - 2] && nums[n - 1]) return ans;
return -1;
}
};
采用枚举法,题目表示必须三个数进行改变,即如果最后nums[n-1]和nums[n-2]个数为1,则不能进行变换,所以单独拿出来分析。
给你一个二维 二进制 数组
grid。请你找出一个边在水平方向和竖直方向上、面积 最小 的矩形,并且满足grid中所有的 1 都在矩形的内部。返回这个矩形可能的 最小面积。
示例 1:
输入: grid = [[0,1,0],[1,0,1]]
输出: 6
解释:
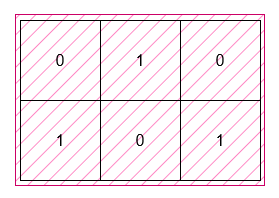
这个最小矩形的高度为 2,宽度为 3,因此面积为
2 * 3 = 6。class Solution {
public:
int minimumArea(vector<vector<int>>& grid) {
int h=0;
int minh=1000;
int l=0;
int minl=1000;
for(int i=0;i<grid.size();i++)
{
for(int j=0;j<grid[i].size();j++)
{
if(grid[i][j])
{
minh=min(minh,i);
h=max(h,i);
l=max(l,j);
minl=min(minl,j);
}
}
}
return (h-minh+1)*(l-minl+1);
}
};
枚举法,取包含1的最大行和最大列,包含1的最小行和最小列。
-
java总结
继承
对于两个类中大量重复的代码,我们可以将这些代码放在另外一个类中,需要时再进行调用。java 的继承通过 extends关键字来实现,实现继承的类被称为子类, 被继承的类被称为父类 。 父类和子类的关系 , 是一种一般和特殊的关系 。 例如水果和苹果的关系 , 苹果继承了水果,苹果是水果的子类,则苹果是一种特殊的水果 。 因为子类是一种特殊的父类 , 因此父类包含的范围总 比子类包含的范围要大, 所以可以认为父类是大类, 而子类是小类 。
定义
Java 里子类继承父类的语法格式如下
修饰符 class 子类 extends 父类 { }:从上面语法格式来看, 定义子类的语法非常简单 , 只需在原来的类定义上增加 extends 父类。
public class Fruit { public double weight; public void info(){ System.out.println( " 我是一个水果! 重"+ weight + "g!"); } }接下来定义fruit的子类Apple
public class Apple extends Fruit { public static void main(String[] args) { Apple a = new Apple() ; a.weight = 56; a.info() ; } }上面的 Apple 类基本只是一个空类,它只包含了一个 mainO方法,但程序中创建了 Apple 对象之后, 可以访问该 Apple 对象的 weight 实例变量和 info()方法,这表明 Apple 对象也具有了 weight 实例变量和 info()方法,这就是继承的作用 。
继承的特点
Java 语言摒弃了 C++ 中难以理解的多继承特征,即每个类最多只有一个直接父类,但支持多层继承 。因为如果继承的多个父类中有相同的方法,子类就无法确定继承哪个方法。
如果定义一个 Java类时并未显式指定这个类的直接父类,则这个类默认父类为Objec 类 。
重写父类的方法
子类扩展了父类,子类是一个特殊的父类。 大部分时候,子类总是以父类为基础 ,额外增加新的成员变量和方法。
但有一种情况例外 : 子类需要重写父类的方法。
例如鸟类都包含了飞翔方法, 其中驼鸟是一种特殊的鸟类,因此驼乌应该是鸟的子类,因此它也将从乌类获得飞翔方法,但这个飞翔方法明显不适合驼鸟,为此,驼鸟需要重写鸟类的方法。
下面程序先定义了 一个Bird类
public class Bird { // Bird 类的 fly() 方法 public void fly() { System.out.println(" 我在天空里自由自在地飞翔. .. "); } }再定义了一个Buird的子类
public class Ostrich extends Bird { //重写 Bird 类的 fly ()方法 public void fly() { System.out.println(" 我只能在地上奔跑 . . . ") ; } public static void main(String[] args) { Ostrich os = new Ostrich( ); //执行 Ostrich对象的 fly ()方法,将输出"我只能在地上奔跑.. . os.fly (); } }执行上面程序,将看到执行os.fly()时执行的不再是 Bird 类的方法,而是执行Ostrich 类的时方法。
这种子类包含与父类同名方法的现象被称为方法重写, 也被称为方法覆盖。可以说子类重写了父类的方法, 也可以说子类覆盖了父类的方法。
方法的重写要遵循 " 两同两小一大"规则,
" 两同"即方法名相同 、 形参列表相同 ;
" 两小"指的是 子类方法返回值类型应比父类方法返回值类型更小或相等 , 子类方法声明抛出的异常类应比父类方法声明抛出的异常类更小或相等;
" 一大 "指的是子类方法的访问权限应比父类方法的访问权限更大或相等。
需要在子类方法中调用父类中被覆盖的方法,则可以使用 super或者父类类名作为调用者来调用父类中被覆盖的方法 。
如果父类方法具 private访问权限,则该方法对其子类是隐藏的,因此其子类无法访问该方法, 也就是无法重写该方法 。
如果子类中定义了 一个与父类 private 方法具有相同的方法名 、 相同的形参列表相同的返回值类型的方法,依然不是重写 , 只是在子类中重新定义了一个新方法.
调用父类的构造器
由于构造方法要与类名一致,所以子类不能继承父类的构造方法。
但子类的构造器可以调用父类构造器的初始化代码。
在一个构造器中调用另一个重载的构造器使用this调用来完成,
在子类构造器中调用父类构造器使用super调用来完成。
看下面程序定义了Base类和 Sub类,其中Sub类是 Base 类的子类,
class Base { public double size; public String name; public Base(double size , String name) { this . size = size ; this . name = name; } } public class Sub extends Base { public String color; public Sub(double size , String name , String color) { super(size , name) ; this.color = color; } public static void main(String[] args) { Sub s = new Sub(5.6 , "测试对象","红色" ) ; System.out.println(s.size + "--" + s.name+"--"+s.color); } }子类的构造方法会先访问父类的无参构造,以防需要父类中数据进行初始化
成员变量
对与父类中的成员变量,子类中是可以进行调用,并赋值。但如果父类中的成员变量被private修饰则不能进行操作。