文章目录
226.翻转二叉树
题目链接:226. 翻转二叉树 - 力扣(LeetCode)
题目描述:给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:
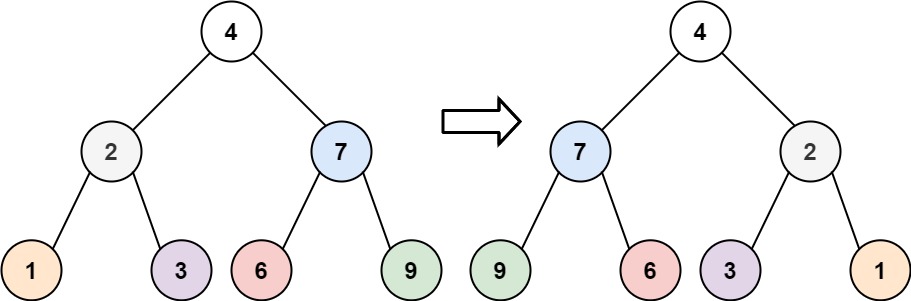
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]示例 2:
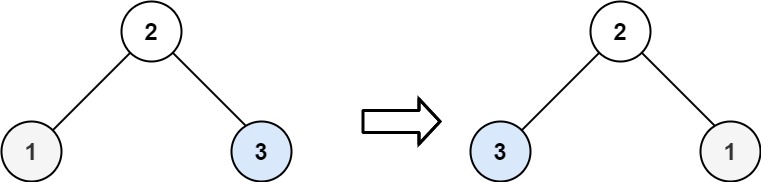
输入:root = [2,1,3]
输出:[2,3,1]示例 3:
输入:root = []
输出:[]提示:
- 树中节点数目范围在
[0, 100]内 -100 <= Node.val <= 100
思路
翻转二叉树,其实就是把每个节点的左右孩子交换一下就可以了,因此只要能遍历二叉树,都可以实现二叉树的翻转
解法一、前序遍历递归
c
struct TreeNode *invertTree(struct TreeNode *root) {
if(!root){
return root;
}
//交换左右孩子
struct TreeNode *node = root->left;
root->left = root->right;
root->right = node;
invertTree(root->left);//递归遍历左子树
invertTree(root->right);//递归遍历右子树
return root;
}解法二、深度优先搜索--迭代
c
struct TreeNode* invertTree(struct TreeNode* root) {
if (!root)
return NULL;
// 存储结点的栈
struct TreeNode** stack =
(struct TreeNode**)malloc(sizeof(struct TreeNode*) * 100);
int stackTop = 0;
// 将根节点入栈
stack[stackTop++] = root;
// 若栈中还有元素(进行循环)
while (stackTop) {
// 取出栈顶元素
struct TreeNode* temp = stack[--stackTop];
// 交换结点的左右孩子
struct TreeNode* tempNode = temp->right;
temp->right = temp->left;
temp->left = tempNode;
// 若当前结点有左右孩子,将其入栈
if (temp->left)
stack[stackTop++] = temp->left;
if (temp->right)
stack[stackTop++] = temp->right;
}
return root;
}101.对称二叉树
题目链接:101. 对称二叉树 - 力扣(LeetCode)
题目描述:给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:

输入:root = [1,2,2,3,4,4,3]
输出:true示例 2:
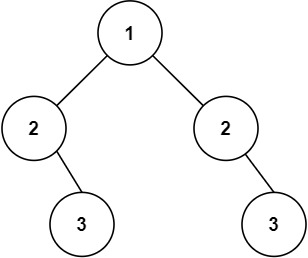
输入:root = [1,2,2,null,3,null,3]
输出:false思路
判断对称二叉树要比较的不是左右节点
二叉树是否对称,其实是比较根节点的左右子树是不是相互翻转的,所以需要遍历两棵树
本题遍历只能是**"后序遍历"**,因为我们要通过递归函数的返回值来判断两个子树的内侧节点和外侧节点是否相等。
解法一、递归
c
bool compare(struct TreeNode* left, struct TreeNode* right) {
if (!left && !right)
return true;
if (left && right && left->val == right->val) {
bool outside = compare(left->left, right->right);// 左子树:左、 右子树:右
bool inside = compare(left->right, right->left); // 左子树:右、 右子树:左
return outside && inside;// 左子树:中、 右子树:中(逻辑处理)
} else {
return false;
}
}
bool isSymmetric(struct TreeNode* root) {
if (!root)
return true;
return compare(root->left, root->right);
}解法二、迭代
把左右两个子树要比较的元素顺序放进一个容器,然后成对取出来进行比较,使用队列和栈均可
c
bool isSymmetric(struct TreeNode *root) {
if(!root) return true;
struct TreeNode *stk[1000];
int top = 0;
stk[top++] = root->left;
stk[top++] = root->right;
while(top){
struct TreeNode *rightNode = stk[--top];
struct TreeNode *leftNode = stk[--top];
if(!rightNode && !leftNode) continue;
if((!leftNode || !rightNode)||(leftNode->val != rightNode->val)){
return false;
}
stk[top++] = leftNode->left;
stk[top++] = rightNode->right;
stk[top++] = leftNode->right;
stk[top++] = rightNode->left;
}
return true;
}104.二叉树的最大深度
题目链接:104. 二叉树的最大深度 - 力扣(LeetCode)
题目描述:给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
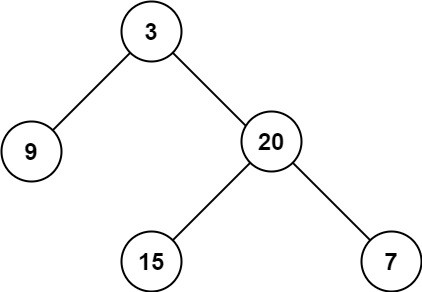
输入:root = [3,9,20,null,null,15,7]
输出:3示例 2:
输入:root = [1,null,2]
输出:2提示:
- 树中节点的数量在
[0, 104]区间内。 -100 <= Node.val <= 100
解法一、深度优先搜索--递归
c
int maxDepth(struct TreeNode *root) {
if (root == NULL) return 0;
return fmax(maxDepth(root->left), maxDepth(root->right)) + 1;
}解法二、广度优先搜索--迭代
通过层次遍历,当遍历到最后一层,层数即二叉树的深度
c
#define MAX_SIZE 10000
int maxDepth(struct TreeNode* root) {
int ans = 0;
if (!root) {
return ans;
}
struct TreeNode* queue[MAX_SIZE];
int rear = 0, front = 0;
queue[rear++] = root;
while (front != rear) {
int size = rear - front;
for (int i = 0; i < size; i++) { // 遍历这一层的所有节点
struct TreeNode* node = queue[front++];
if (node->left)
queue[rear++] = node->left;
if (node->right)
queue[rear++] = node->right;
}
ans++;//层数+1
}
return ans;
}111.二叉树的最小深度
题目链接:111. 二叉树的最小深度 - 力扣(LeetCode)
题目描述:给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
**说明:**叶子节点是指没有子节点的节点。
示例 1:
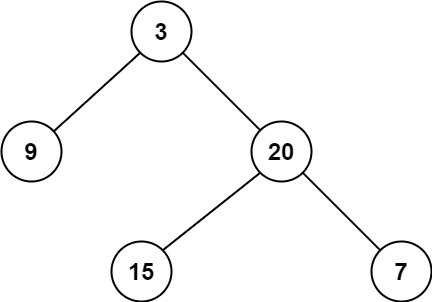
输入:root = [3,9,20,null,null,15,7]
输出:2示例 2:
输入:root = [2,null,3,null,4,null,5,null,6]
输出:5提示:
- 树中节点数的范围在
[0, 105]内 -1000 <= Node.val <= 1000
解法一、深度优先搜索--递归
对于每一个非叶子节点,我们只需要分别计算其左右子树的最小叶子节点深度。这样就将一个大问题转化为了小问题,可以递归地解决该问题,需要注意的是只有当左右孩子都为空的时候,才说明遍历的最低点了。如果其中一个孩子为空则不是最低点
c
int minDepth(struct TreeNode *root) {
if (root == NULL) {
return 0;
}
if (root->left == NULL && root->right == NULL) {
return 1;
}
int min_depth = INT_MAX;
if (root->left != NULL) {
min_depth = fmin(minDepth(root->left), min_depth);
}
if (root->right != NULL) {
min_depth = fmin(minDepth(root->right), min_depth);
}
return min_depth + 1;
}解法二、广度优先搜索--迭代
c
#define MAX_SIZE 100000
int minDepth(struct TreeNode* root) {
int ans = 0;
if (!root) {
return ans;
}
struct TreeNode* queue[MAX_SIZE];
int rear = 0, front = 0;
queue[rear++] = root;
while (front != rear) {
int size = rear - front;
ans++; // 层数+1
for (int i = 0; i < size; i++) { // 遍历这一层的所有节点
struct TreeNode* node = queue[front++];
if (node->left)
queue[rear++] = node->left;
if (node->right)
queue[rear++] = node->right;
// 当左右孩子都为空的时候,说明是最低点的一层了,退出
if (!node->left && !node->right) {
return ans;
}
}
}
return ans;
}