【Godot4.2】Godot中的贝塞尔曲线

概述

通过指定平面上的多个点，然后顺次连接，我们可以得到折线段，如果闭合图形，就可以获得多边形。通过向量旋转我们可以获得圆等特殊图形。

但是对于任意曲线，我们无法使用简单的方式来获取其顶点，好在计算机大神们已经发明了贝塞尔曲线这样的算法。

本篇就介绍如何在Godot中绘制贝塞尔曲线，并通过设定控制点来精确控制曲线的走向。

（原文写于2024年4月，内容持续改进和扩充中）

基础原理

在实际上手绘制之前，让我们先来理解一下贝塞尔曲线的求点原理与本质------向量插值。

二次贝塞尔曲线

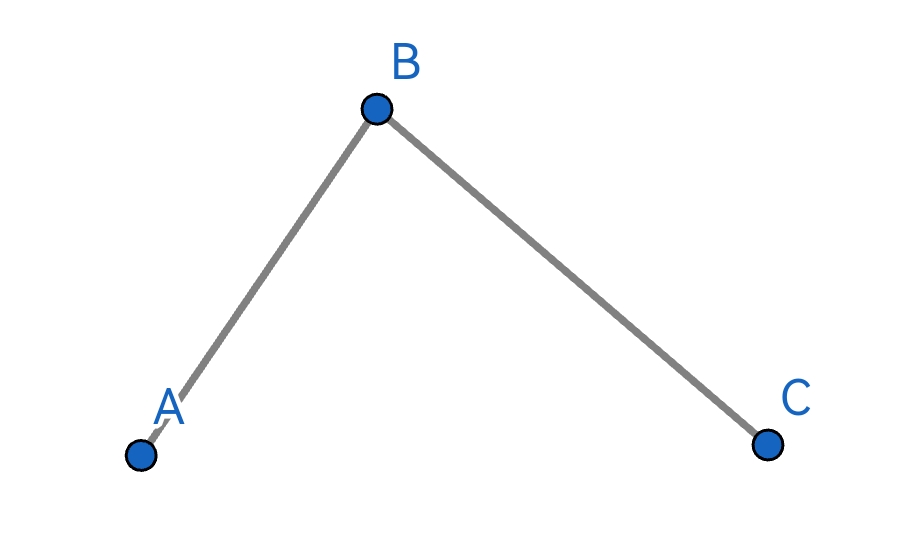
在平面上有三个点A、B、C：

AB相连，形成一个向量 A B ⃗ \vec{AB} AB ，BC相连，形成另一个向量 B C ⃗ \vec{BC} BC ；
对 A B ⃗ \vec{AB} AB 和 B C ⃗ \vec{BC} BC 同步进行0.0到1.0插值，设插值变量为t。
在插值的每一时刻，会从 A B ⃗ \vec{AB} AB 和 B C ⃗ \vec{BC} BC 上各获得一个点D和E。
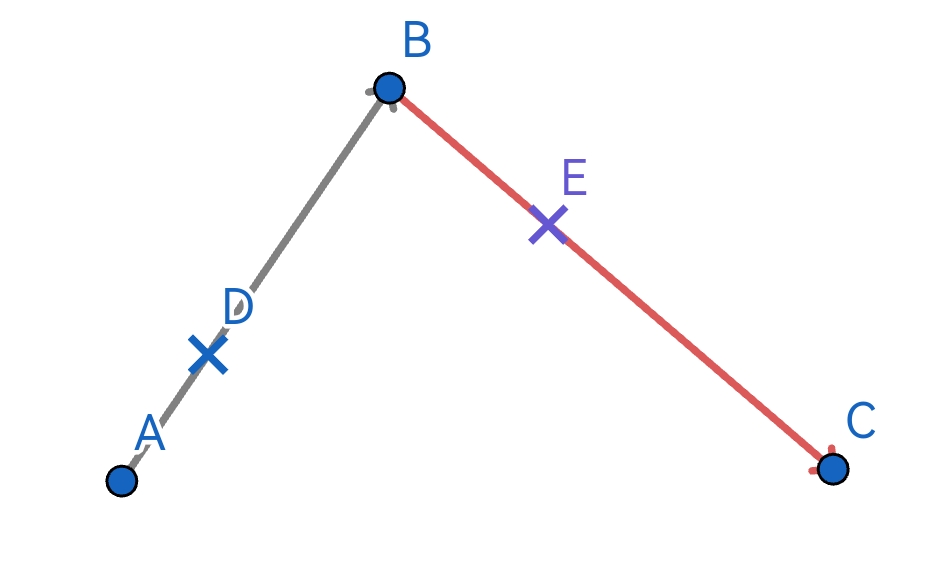
连接DE，对 D E ⃗ \vec{DE} DE 进行0.0到1.0插值，而且插值与此时的t一致。则获得一个点F。
也就是说，同步对 A B ⃗ \vec{AB} AB 和 B C ⃗ \vec{BC} BC 、 D E ⃗ \vec{DE} DE 进行0.0到1.0插值。

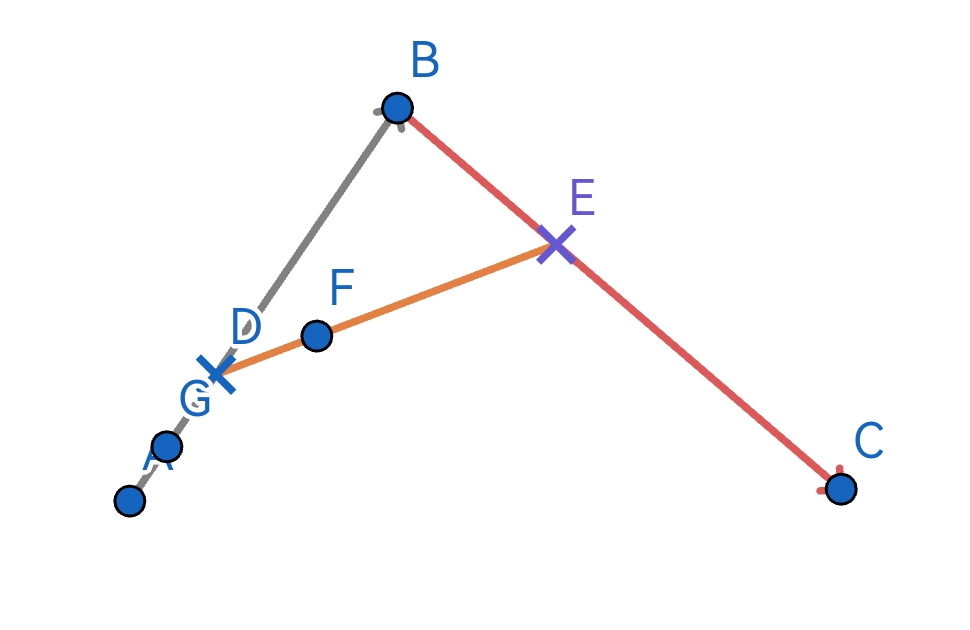
从 D E ⃗ \vec{DE} DE 插值获取的所有点F连起来就是一条由A到B的贝塞尔曲线。整个插值过程也就是官方文档中的这张动图：

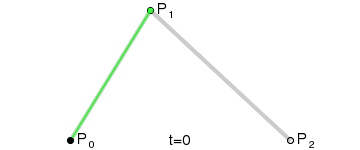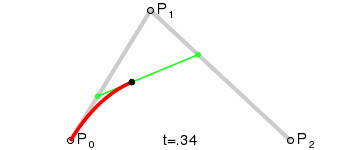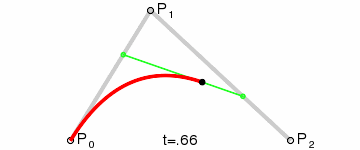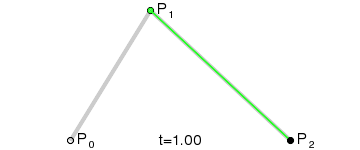
所以二次贝塞尔曲线是同时进行三个向量插值获得的点的集合。

三次贝塞尔曲线

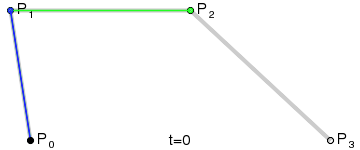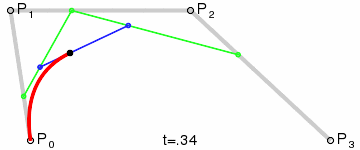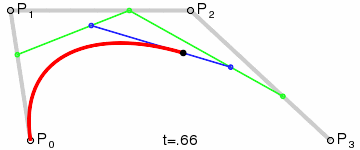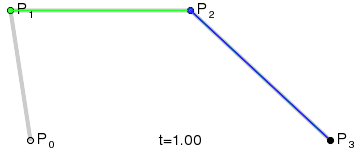
平面上四个点A、B、C、D：

分别组成三个向量 A B ⃗ \vec{AB} AB 、 B C ⃗ \vec{BC} BC 和 C D ⃗ \vec{CD} CD
在三个向量上同步插值获得三个点E、F、G
EF和FG相连，组成向量 E F ⃗ \vec{EF} EF 、 F G ⃗ \vec{FG} FG
在 E F ⃗ \vec{EF} EF 、 F G ⃗ \vec{FG} FG 上同步插值获得点H和I
E F ⃗ \vec{EF} EF 上同步插值获得点J
整个同步插值过程获得的点J的集合，顺序相连，绘制处的就是三次贝塞尔曲线 。

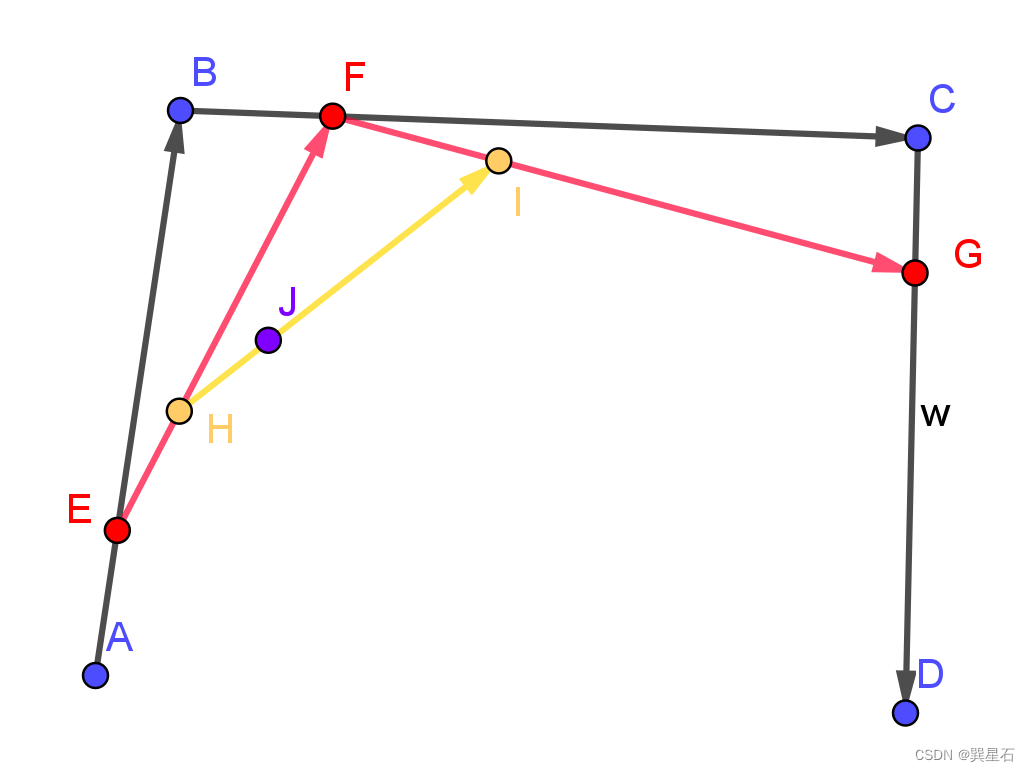
动态过程如下（也就是官方文档的动图）：

在Godot中实际绘制贝塞尔曲线

在Godot中实际上并不需要我们编写自己的贝塞尔曲线插值求点函数，Vector2类型的bezier_interpolate()方法可以让我们轻松的获取相应顶点和控制点设置下的贝塞尔曲线点。它的定义如下：

swift 复制代码

bezier_interpolate(control_1: Vector2, control_2: Vector2, end: Vector2, t: float) -> Vector2

control_1和control_2分别为控制点1 和控制点2
end可以理解为第二个点
t是0.0到1.0的插值，也可以理解为一个百分比或偏移量

bezier_interpolate()的用法就是：

swift 复制代码

p1.bezier_interpolate(c1,c2,p2,t)

其中：

p1是贝塞尔曲线起点，p2是贝塞尔曲线终点
c1,c2分别为控制点1 和控制点2
t是百分比

所以我们想要求一段贝塞尔曲线，就需要指定4个点，其中2个是起止点，另外2个是控制点。并使用一个for循环来进行插值，求取整个过程中的点。

最后再使用Godot内置的绘图函数draw_polyline()来绘制。

我们看一个实例：

swift 复制代码

extends Node2D

var p1 = Vector2(100,100)   # 起点
var p2 = Vector2(200,200)   # 终点
var ctl_1 = Vector2(100,0)  # 控制点1
var ctl_2 = Vector2(100,0)  # 控制点2

var points:PackedVector2Array = []   # 曲线点集合
var steps = 100;                     # 点的数目，越多曲线越平滑

var curve_color:= Color.WHITE       # 曲线绘制颜色
var ctl_color:= Color.AQUAMARINE    # 控制点和连线绘制颜色

func _ready() -> void:
	# 求曲线点集
	for i in range(steps+1):
		var p = p1.bezier_interpolate(p1+ctl_1,p2-ctl_2,p2,i/float(steps))
		points.append(p)


func _draw() -> void:
	# 绘制控制点
	draw_arc(p1+ctl_1,2,0,TAU,10,ctl_color,1)
	draw_arc(p2-ctl_2,2,0,TAU,10,ctl_color,1)
	# 绘制曲线端点与控制点的连线
	draw_line(p1,p1+ctl_1-Vector2(1,0),ctl_color,1)
	draw_line(p2,p2-ctl_1+Vector2(1,0),ctl_color,1)
	# 绘制贝塞尔曲线
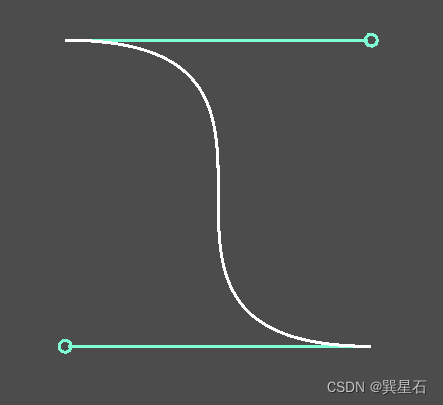
	draw_polyline(points,curve_color,1)

上面的代码中：

我们首先声明变量保存起点、终点和两个控制点的坐标
然后申明变量points用于存储插值获取的贝塞尔曲线上的点
steps变量用于存储总共插值的步数，也就是获得的曲线上点的个数，步数越多，求得的点越多，最终绘制的曲线越平滑
申明两个变量来分别存储曲线和控制点的颜色。
在_ready()中我们执行一个for循环来插值steps次，来获取指定的起点、终点、控制点下的贝塞尔曲线上的点，并存储到变量points中
_draw()在场景运行时会被自动调用，用来实际的绘制出曲线和控制点

最终绘制结果如下：

导数

Vector2类型提供了一个名叫bezier_derivative()的方法，用来求贝塞尔曲线上t处的"导数"。

经过实际测试，这个所谓的"导数"是一个点，连接贝塞尔曲线上t处的点与该点，刚好是一个切线段。

我们以下面的代码进行测试：

swift 复制代码

extends Node2D

var p1 = Vector2(100,100)   # 起点
var p2 = Vector2(200,200)   # 终点
var ctl_1 = Vector2(50,0)  # 控制点1
var ctl_2 = Vector2(50,0)  # 控制点2

var points:PackedVector2Array = []   # 曲线点集合
var ds:PackedVector2Array = []       # 曲线点导数集合
var steps = 100;                     # 点的数目，越多曲线越平滑

var curve_color:= Color.WHITE       # 曲线绘制颜色
var ctl_color:= Color.AQUAMARINE    # 控制点和连线绘制颜色

func _ready() -> void:
	# 求曲线点集
	for i in range(steps+1):
		var p = p1.bezier_interpolate(p1+ctl_1,p2-ctl_2,p2,i/float(steps))
		points.append(p)
		var d = p1.bezier_derivative(p1+ctl_1,p2-ctl_2,p2,i/float(steps))
		ds.append(d)


func _draw() -> void:
	draw_polyline(points,curve_color,1)
	var i = 0
	draw_line(points[i],points[i]+ds[i],ctl_color,1)
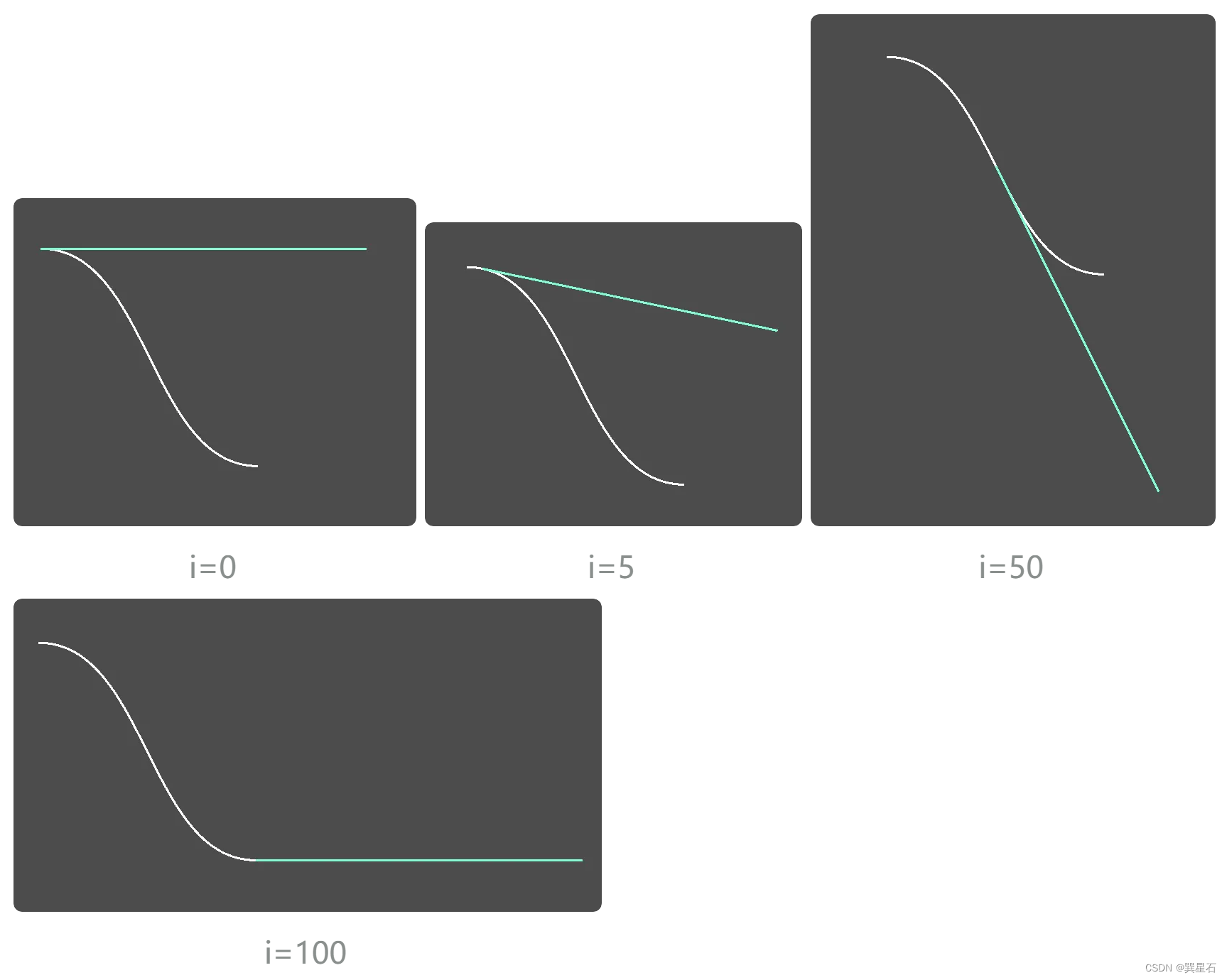
	print(points[i]," ",points[i]+ds[i])

其中i是指曲线上点的索引，不同的i可以从points[i]中获取代表在i/float(steps)处的点。

以下是一些i值下对应点与"导数"点连线的情况：

将极坐标点函数运用于贝塞尔控制点

swift 复制代码

# 极坐标点函数 - 通过角度和长度定义一个点
func pVector2(angle:float = 0.0,length:float =0.0) -> Vector2:
	var dir = Vector2.RIGHT.rotated(deg_to_rad(angle))
	return dir * length

Vector2很难直观的表达方向和距离信息，pVector2则可以，所以在设定贝塞尔控制点时，可以使用极坐标点函数。

swift 复制代码

extends Node2D

var p1 = Vector2(100,100)   # 起点
var p2 = Vector2(200,200)   # 终点
var ctl_1 = pVector2(0,50)  # 控制点1
var ctl_2 = pVector2(180,50)  # 控制点2

var points:PackedVector2Array = []   # 曲线点集合
var steps = 100;                     # 点的数目，越多曲线越平滑

var curve_color:= Color.WHITE       # 曲线绘制颜色
var ctl_color:= Color.AQUAMARINE    # 控制点和连线绘制颜色

func _ready() -> void:
	# 求曲线点集
	for i in range(steps+1):
		var p = p1.bezier_interpolate(p1+ctl_1,p2+ctl_2,p2,i/float(steps))
		points.append(p)


func _draw() -> void:
	# 绘制控制点
	draw_arc(p1+ctl_1,2,0,TAU,10,ctl_color,1)
	draw_arc(p2+ctl_2,2,0,TAU,10,ctl_color,1)
	# 绘制曲线端点与控制点的连线
	draw_line(p1,p1+ctl_1-Vector2(1,0),ctl_color,1)
	draw_line(p2,p2-ctl_1+Vector2(1,0),ctl_color,1)
	# 绘制贝塞尔曲线
	draw_polyline(points,curve_color,1)

绘制效果如下：

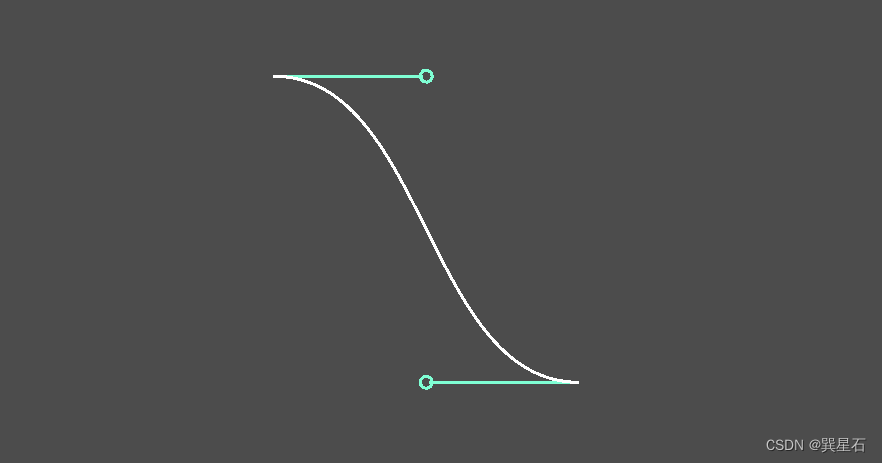
可以看到，我们可以更直观的设定控制点在起点或终点的哪个方向，以及多长。

贝塞尔曲线函数

我们可以将贝塞尔曲线上点的求取过程封装为一个函数，这样就可以直接调用。

swift 复制代码

# 求两点之间的贝塞尔曲线
func bezier_curve(p1:Vector2,p2:Vector2,ctl_1:=Vector2(),ctl_2:=Vector2(),points_count:=10) -> PackedVector2Array:
	var points:PackedVector2Array = []
	# 求曲线点集
	for i in range(points_count+1):
		var p = p1.bezier_interpolate(p1+ctl_1,p2+ctl_2,p2,i/float(points_count))
		points.append(p)
	return points

同样我们可以编写一个贝塞尔曲线绘制函数，用来直接在CanvasItem上调用和绘制：

swift 复制代码

# 绘制贝塞尔曲线
func draw_bezier_curve(canvas:CanvasItem,p1:Vector2,p2:Vector2,ctl_1:=Vector2(),ctl_2:=Vector2(),points_count:=10):
	var points:PackedVector2Array = []   # 曲线点集合
	points.append_array(bezier_curve(p1,p2,ctl_1,ctl_2,points_count))
	# 绘制控制点
	draw_arc(p1+ctl_1,2,0,TAU,10,ctl_color,1)
	draw_arc(p2+ctl_2,2,0,TAU,10,ctl_color,1)
	# 绘制曲线端点与控制点的连线
	draw_line(p1,p1+ctl_1-Vector2(1,0),ctl_color,1)
	draw_line(p2,p2+ctl_2-Vector2(1,0),ctl_color,1)
	# 绘制贝塞尔曲线
	draw_polyline(points,curve_color,1)

测试代码：

swift 复制代码

extends Node2D

var p1 = Vector2(100,100)   # 点1
var p2 = Vector2(200,200)   # 点2
var p3 = Vector2(400,300)   # 点3
var ctl_1 = pVector2(-90,100)  # 控制点1
var ctl_2 = pVector2(-45,100)  # 控制点2
var ctl_3 = pVector2(135,100)  # 控制点3
var ctl_4 = pVector2(45,100)  # 控制点4


var steps = 100;                     # 点的数目，越多曲线越平滑

var curve_color:= Color.WHITE       # 曲线绘制颜色
var ctl_color:= Color.AQUAMARINE    # 控制点和连线绘制颜色


func _draw() -> void:
	draw_bezier_curve(self,p1,p2,ctl_1,ctl_2,50)
	draw_bezier_curve(self,p2,p3,ctl_3,ctl_4,50)

可以看到：

通过给定连续的点和控制点，可以创建连续的贝塞尔曲线
在连接处，通过使用完全反向的控制点，可以让贝塞尔曲线连接处更丝滑

多点连续贝塞尔曲线绘制函数

通过以PackedVector2Array形式传入多个关键点和控制点，我们便可以更轻松的绘制多点连续贝塞尔曲线。

函数如下：

swift 复制代码

# 绘制由多个点和控制点顺序组成的贝塞尔曲线
func draw_points_bezier_curve(canvas:CanvasItem,points:PackedVector2Array,ctls:PackedVector2Array,points_count:=10):
	# 求所有点之间的贝塞尔曲线点
	for i in range(points.size() -1):
		var seg = [points[i],points[i+1]]        # 线段
		var ctl = [ctls[i * 2],ctls[i * 2 + 1]]  # 控制点
		draw_bezier_curve(canvas,seg[0],seg[1],ctl[0],ctl[1],points_count)

测试代码：

swift 复制代码

extends Node2D

# 曲线关键点
var points:PackedVector2Array = [
	Vector2(100,100),
	Vector2(200,200),
	Vector2(400,300)
]
# 控制点
var ctls:PackedVector2Array = [
	pVector2(-90,100),
	pVector2(-45,100),
	pVector2(135,100),
	pVector2(45,100)
]

var curve_color:= Color.WHITE       # 曲线绘制颜色
var ctl_color:= Color.AQUAMARINE    # 控制点和连线绘制颜色


func _draw() -> void:
	draw_points_bezier_curve(self,points,ctls,50)

绘制效果：

绘制心形曲线

通过利用上面的多点连续贝塞尔曲线绘制函数，我们便可以通过一系列顶点和控制点数据，绘制处一个简单的心形曲线。

swift 复制代码

extends Node2D

# 曲线关键点
var points:PackedVector2Array = [
	Vector2(100,100),
	Vector2(100,200),
	Vector2(100,100),
]
# 控制点
var ctls:PackedVector2Array = [
	pVector2(-38,120),
	pVector2(-25,100),
	pVector2(-155,100),
	pVector2(-142,120),
]

绘制效果：

基于贝塞尔曲线的特殊图形参数化函数

一些复杂但常见的图形比如心形等，起始可以用几个坐标点和控制点数据描述和复现。

因此完全可以基于基础的图形绘制函数结合贝塞尔曲线，来生成复杂的图形。

甚至可以编写相应的函数来快速生成某种图形。