leetcode-105. 从前序与中序遍历序列构造二叉树

manba_2024-07-23 16:48

题目描述

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历 ， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

复制代码

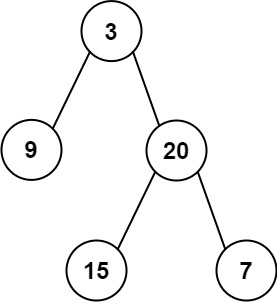
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

复制代码

输入: preorder = [-1], inorder = [-1]
输出: [-1]

思路

剑指offer重建二叉树-CSDN博客

1）递归地按照前序的顺序，制作成根节点

2）在中序中找到根节点的索引，按照其索引将树分为左子树和右子树

3）直到前序和中序序列没有

4）返回根节点

python 复制代码

# Definition for a binary tree node.
class TreeNode(object):
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
class Solution(object):
    def buildTree(self, preorder, inorder):
        """
        :type preorder: List[int]
        :type inorder: List[int]
        :rtype: TreeNode
        """
        if not preorder or not inorder:
            return None
        root = TreeNode(preorder[0])
        index = inorder.index(root.val)
        root.left = self.buildTree(preorder[1:index+1],inorder[:index])
        root.right = self.buildTree(preorder[index+1:],inorder[index+1:])
        return root

def printTreeMidOrder(root, res):
    if not root:
        return None
    if root.left:
        printTreeMidOrder(root.left, res)
    res.append(root.val)
    if root.right:
        printTreeMidOrder(root.right, res)

if __name__ == '__main__':
    s = Solution()
    pre = [1, 2, 4, 7, 3, 5, 6, 8]
    tin = [4, 7, 2, 1, 5, 3, 8, 6]
    root = s.buildTree(pre, tin)
    # 打印中序遍历结果
    res = []
    printTreeMidOrder(root, res)
    print(res)