目录
2.2记录快慢指针相遇节点,与头结点一起向后走,相遇点为入环点
1.判断链表是否带环
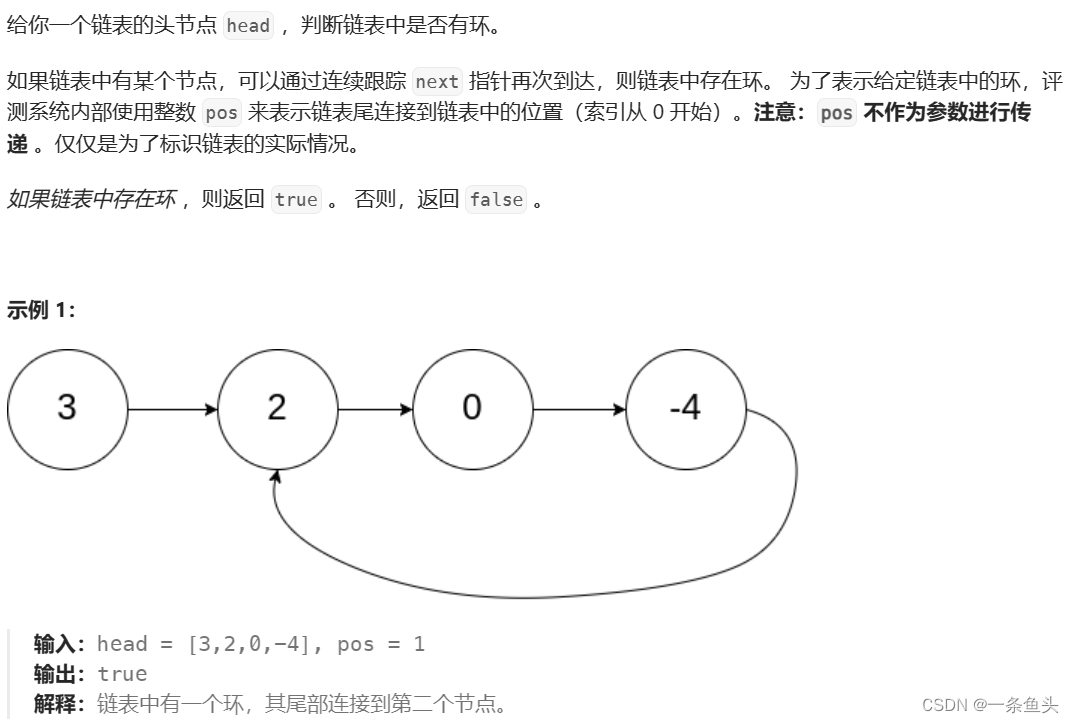
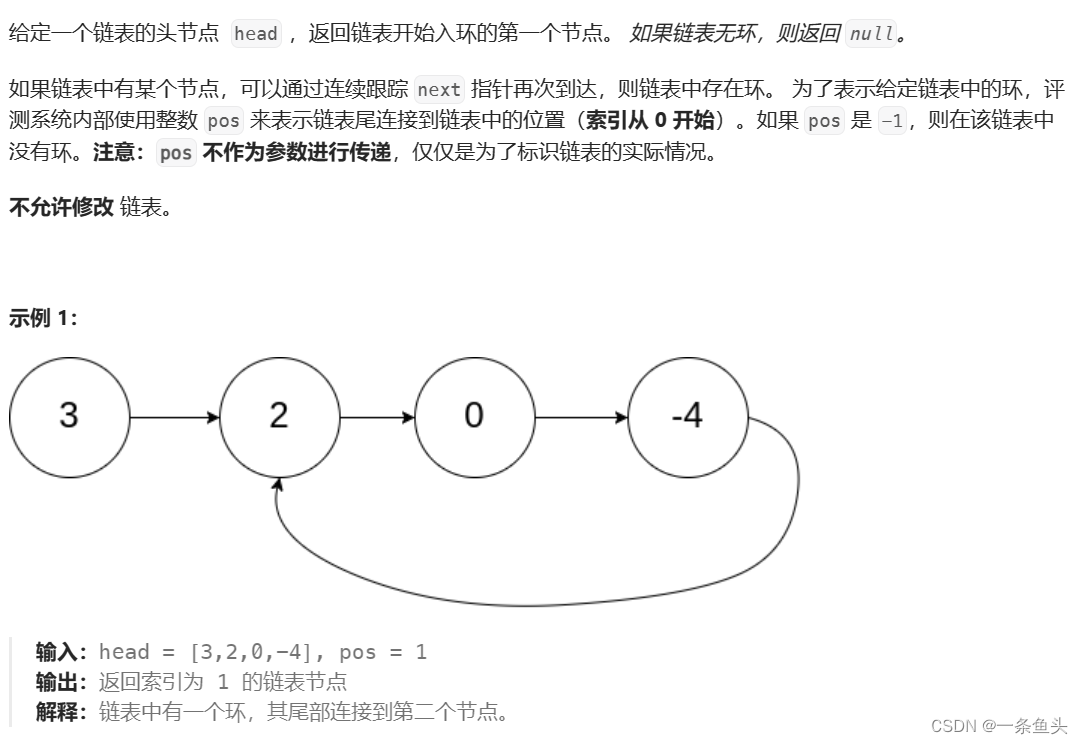
这道题目较为简单,我们知道,带环链表区别于不带环链表的一大特点就是它的最后一个节点指向链表中的某个节点,而不是NULL。
从这一点出发,我们可以探索出这道题的核心解法,定义一对快慢指针(slow和fast)在链表里面往下走,抓住带环链表往下走走不到头的特点,我们思考,大概率在慢指针入环后快指针会重新追上慢指针。
好,那我们接下来就可以探讨一下这种方案的可行性啦~
1.1快指针的速度为慢指针的2倍
也就是慢指针走一步,快指针走两步这种情况。
依照我们正常的认知,这种情况非常可行~
那事实真是如此吗?哈哈,还真是如此!
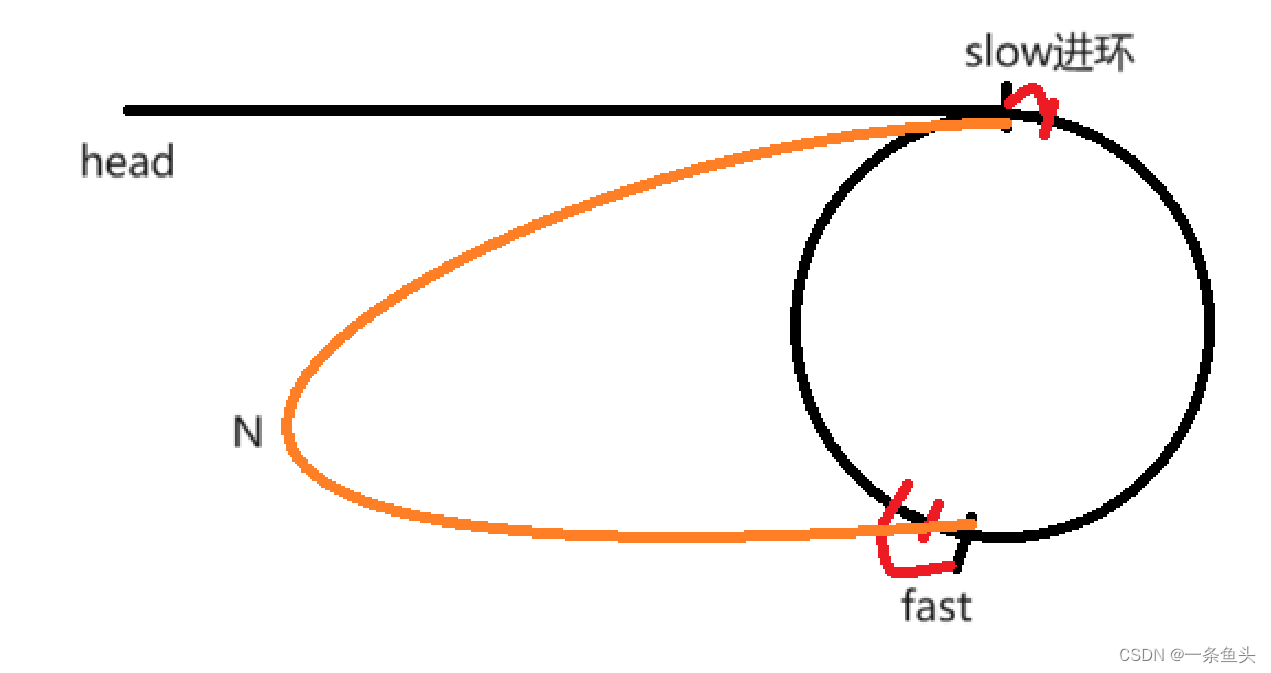
如图所示,设slow进环时,fast与slow相距N个节点,
进行下一步:
slow走一步,fast走两步,相距N-1个节点
slow走一步,fast走两步,相距N-2个节点
slow走一步,fast走两步,相距N-3个节点
.............
slow走一步,fast走两步,相距1个节点
slow走一步,fast走两步,相遇。
通过上述分析,快指针的速度为慢指针的2倍是完全可行的~
1.2快指针的速度为慢指针的3倍
也就是说慢指针走一步,快指针走三步。
经过第一种情况的讨论,你是否觉得这种情况不成立呢?
别着急,我们先来分析一波~
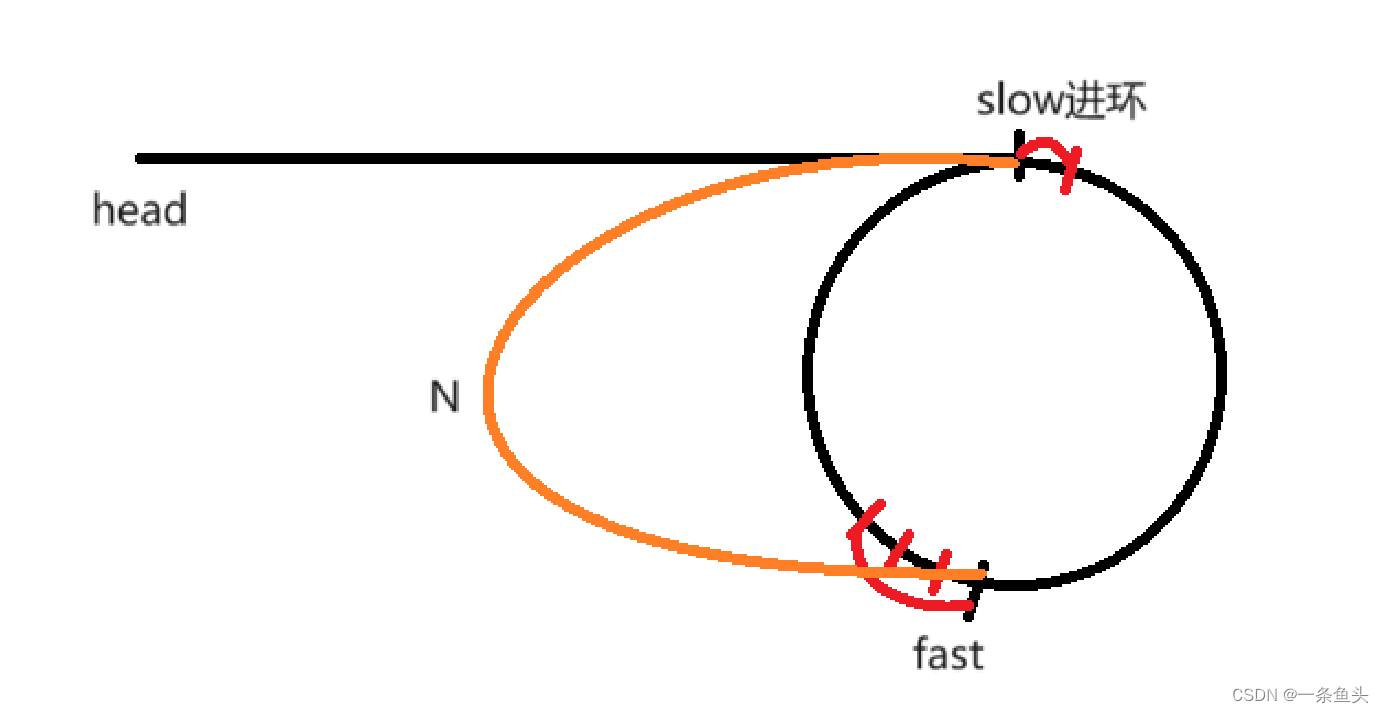
如图所示,设slow进环时,fast与slow相距N个节点,
此时要分为两种情况讨论
1.当N为偶数时,进行下一步:
slow走一步,fast走三步,相距N-2个节点
slow走一步,fast走三步,相距N-4个节点
slow走一步,fast走三步,相距N-6个节点
...........
slow走一步,fast走三步,相距2个节点
slow走一步,fast走三步,相遇
2.当N为奇数时,进行下一步:
slow走一步,fast走三步,相距N-2个节点
slow走一步,fast走三步,相距N-4个节点
slow走一步,fast走三步,相距N-6个节点
...........
slow走一步,fast走三步,相距1个节点
slow走一步,fast走三步,相距-1个节点
看到相距-1个节点,此时出现的状况就是fast跳过了slow ,并没有遇上,所以后续是否能遇上还需要接着讨论。
那接下来我们就设环的总长度为C,此时两个指针相距C-1。
此时还要分为两种情况讨论
1.当C为奇数,即C-1为偶数时,进行下一步:
slow走一步,fast走三步,相距C-3个节点
slow走一步,fast走三步,相距C-5个节点
slow走一步,fast走三步,相距C-7个节点
...........
slow走一步,fast走三步,相距2个节点
slow走一步,fast走三步,相遇
2.当C为偶数,即C-1为奇数时,进行下一步:
slow走一步,fast走三步,相距C-3个节点
slow走一步,fast走三步,相距C-5个节点
slow走一步,fast走三步,相距C-7个节点
...........
slow走一步,fast走三步,相距1个节点
slow走一步,fast走三步,相距-1个节点
好,看到此时再次出现-1个节点,大部分人就可以笃定, "快指针的速度为慢指针的3倍"这种解法在N为奇数且C为偶数时,存在无法相遇的情况。
BUT!
请看以下分析!
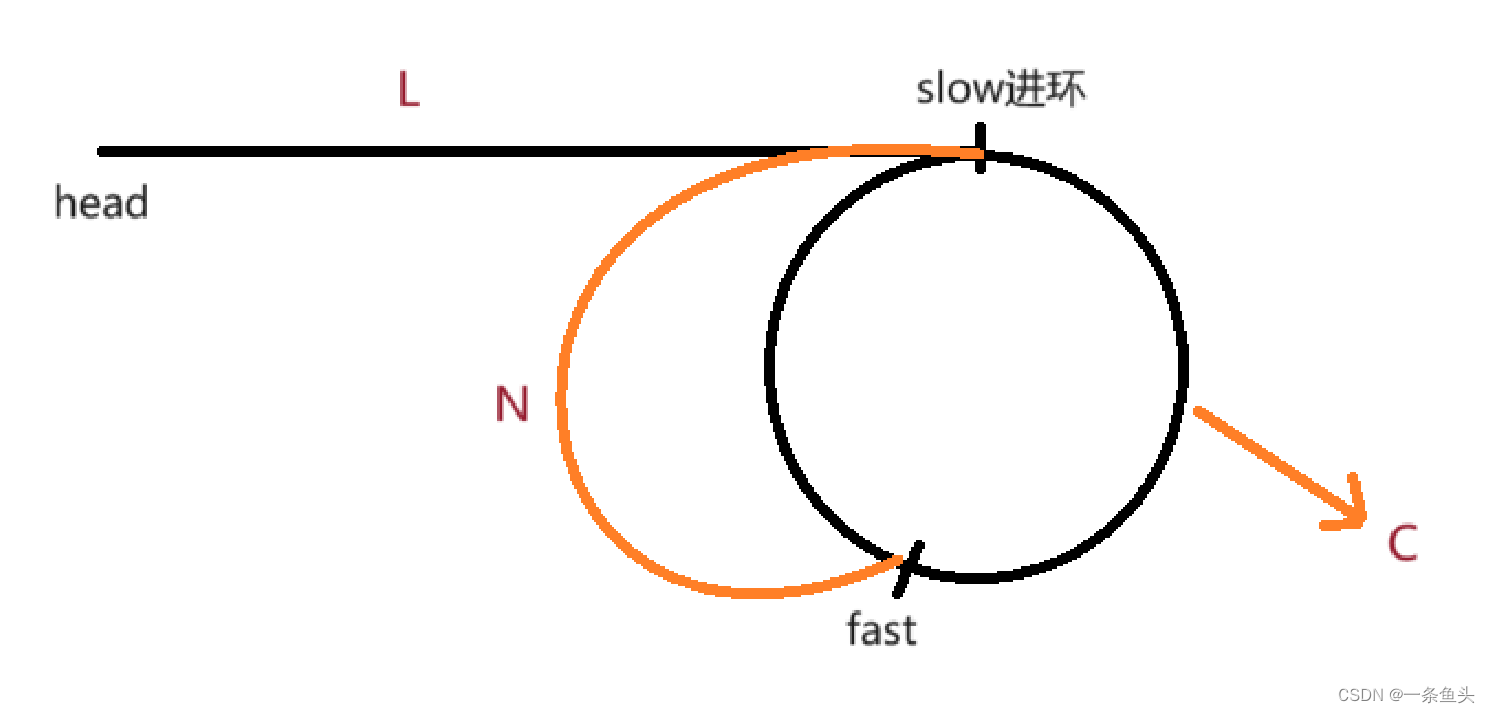
在slow进环时,设前面没有环的部分长度为L,fast与slow相距N,环的长度为C,fast在环里面转了x圈。
根据fast走的长度是slow的三倍这个关系,列出以下等式
3L=L+x*C+(C-N)
化简:2L=C*(x-1)-N
这里复习一下数学:奇数*奇数=奇数;奇数*偶数=偶数;偶数*偶数=偶数
可见,2L一定是个偶数,当C为偶数,N为奇数时,得到的结果一定为奇数,与2L为偶数相违背!
故:"在N为奇数且C为偶数时" 这种情况不存在!
即:快指针的速度为慢指针的3倍,可行!
之后往下的速度为4、5...倍关系就不一一展开讨论啦~
使用2倍方法的代码如下:
cpp
typedef struct ListNode ListNode;
bool hasCycle(struct ListNode *head) {
ListNode*fast,*slow;
fast=slow=head;
while(fast&&fast->next)
{
slow=slow->next;
fast=fast->next->next;
if(slow==fast)
{
return true;
}
}
return false;
}2.找出带环链表开始入环的第一个节点
这道题目是在上道题目基础上的延伸,想要找出环形链表入环的第一个节点可不能再用单纯只使用快慢指针了,因为快慢指针相遇点并不是环形链表入环的第一个节点。
那么该怎么写呢?
利用 "快指针的速度为慢指针的2倍" 这里提供两种思路:
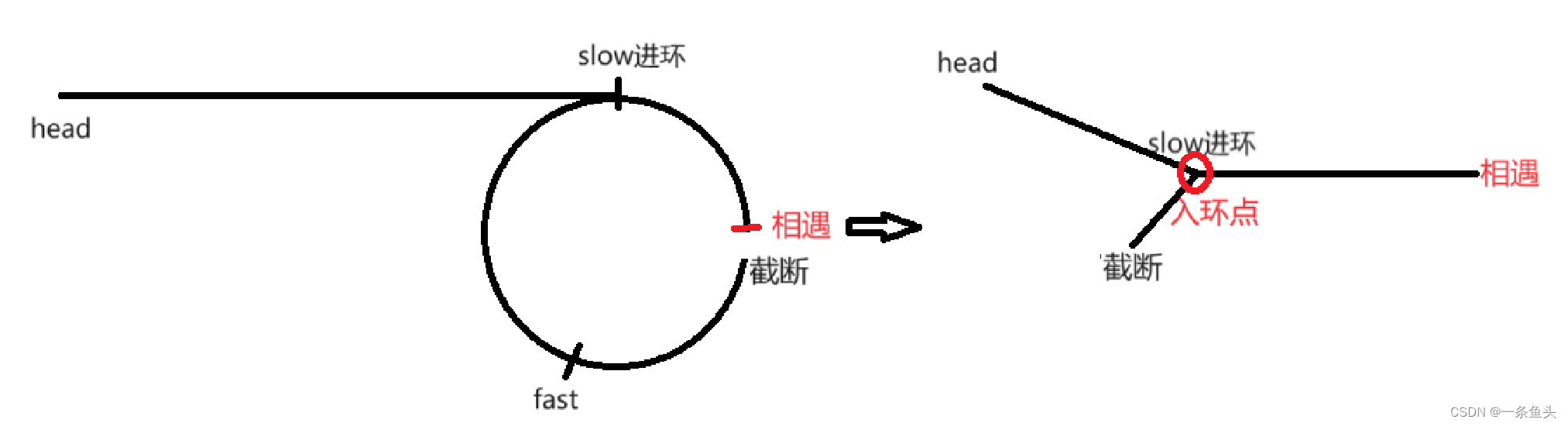
2.1将快慢指针相遇的节点与后面分开,构造交叉链表
这里首先说明一点:在slow入环之后,fast走的圈数不会超过两圈就能与slow相遇。所以相遇节点一定不是入环点!
这样的话,利用 "将快慢指针相遇的节点与后面分开,构造交叉链表" 这一思路,通过找到交叉链表的交叉点,就能找到入环点。
缺点就是需要的指针稍微有点多
2.2记录快慢指针相遇节点,与头结点一起向后走,相遇点为入环点
这种方法正常来说想不到,因为这是根据简单的数学推理得出
推理过程如下:
(这部分与前面一样)在slow进环时,设前面没有环的部分长度为L,fast与slow相距N,环的长度为C,fast在环里面转了x圈。
根据fast走的长度是slow的两倍这个关系,列出以下等式
2L=L+x*C+(C-N)
化简:L=x*C+(C-N)
其中C-N代表相遇节点距离入环点剩下的节点。
通过等式我们可以推理出:
当x=0时,L=C-N,刚好相遇节点与头结点距离入环点的长度相同。
当x!=0时,相遇节点与头结点距离入环点相差x个圈数,说明L相对较长,那么等头指针走完多余的x*C长度后,剩下的距离就是C-N了。
因此这种方法成立。
代码如下:
cpp
typedef struct ListNode ListNode;
struct ListNode *detectCycle(struct ListNode *head) {
ListNode*fast,*slow;
fast=slow=head;
while(fast&&fast->next)
{
slow=slow->next;
fast=fast->next->next;
if(slow==fast)
{
ListNode*prev=head;
while(prev!=slow)
{
prev=prev->next;
slow=slow->next;
}
return prev;
}
}
return NULL;
}OK~ 本次OJ题目分享就到这里
希望收获小伙伴们的支持!!!!
有问题欢迎在评论区评论哦~