栈
- 1.删除字符串中的所有相邻重复项
- 2.比较含退格的字符串
- [3.基本计算器 II](#3.基本计算器 II)
- 4.字符串解码
- 5.验证栈序列

点赞 👍👍收藏 🌟🌟关注 💖💖
你的支持是对我最大的鼓励,我们一起努力吧!😃😃
栈并不是很难的数据结构,我们就可以使用数组模拟出来。但是某些问题难就难在看到这道题的时候能不能想到用栈来解决。如果能想到你会发现这些题本质就是借用栈模拟一下就可以了。
1.删除字符串中的所有相邻重复项
题目链接: 1047. 删除字符串中的所有相邻重复项
题目描述:
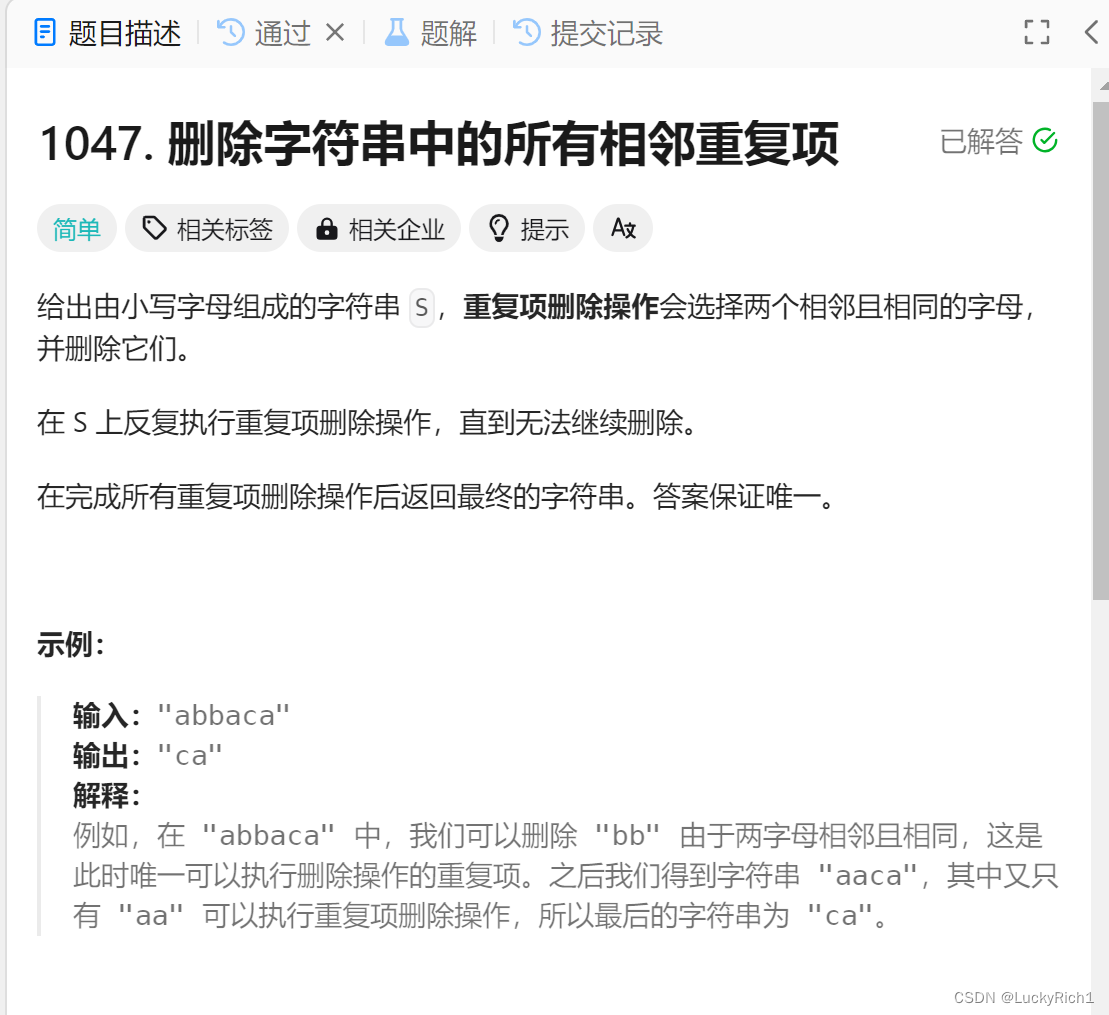
算法原理:
我们可以把这个字符串看成一个往下坠的字符串,如同消消乐一般。相同的就消掉的。

这个过程很明显就是栈的应用。
解法:利用栈做一下模拟即可
用栈模拟一下发现最后栈中的元素就是最终答案。
栈空或者栈顶元素和要入栈的元素不一样直接入栈,反过来就出栈,继续下一个。
但是这道题是要我们返回string,这样做还需要把栈中的元素取出来放到string里。
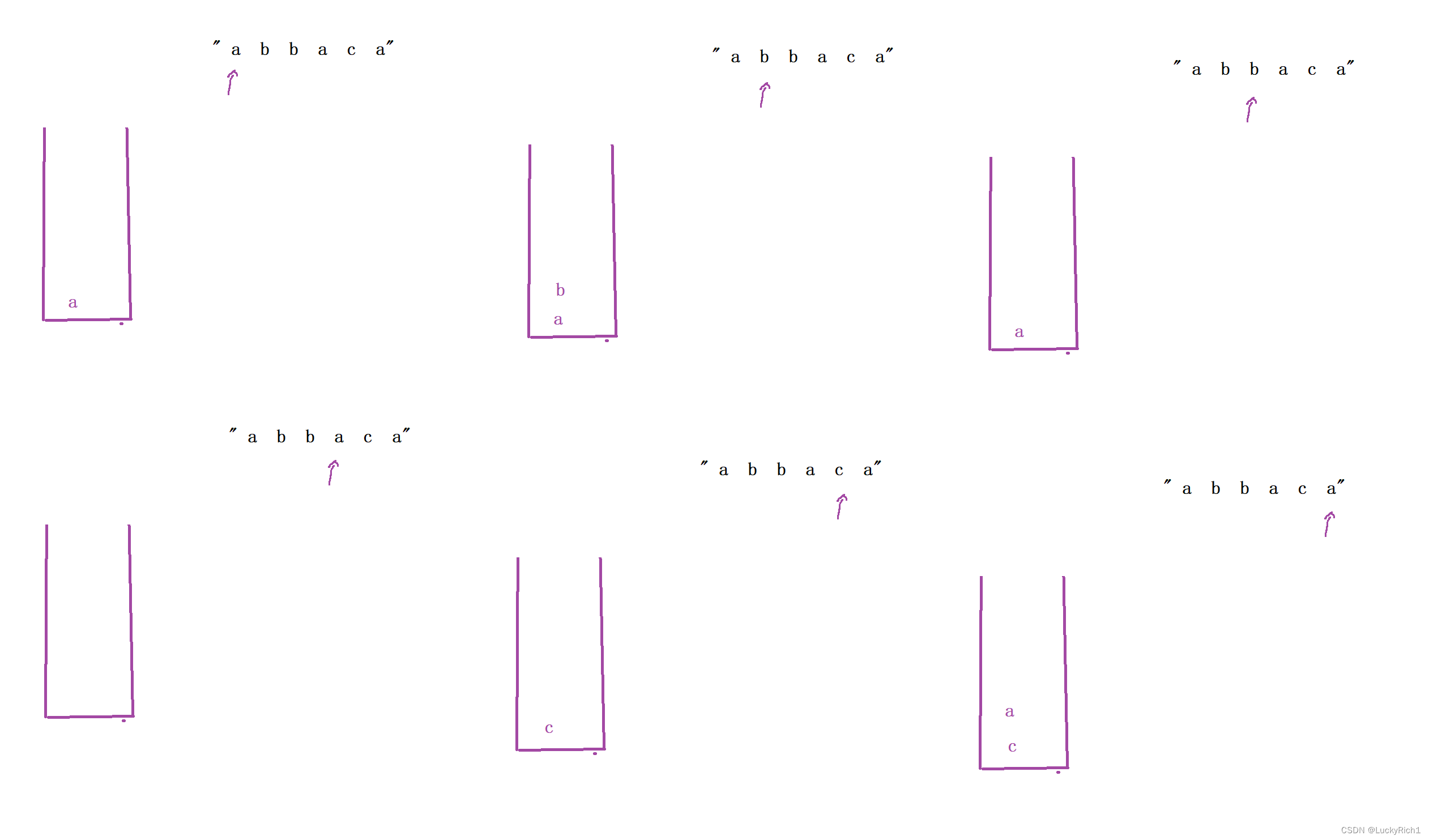
所以我们可以用string模拟一下栈。
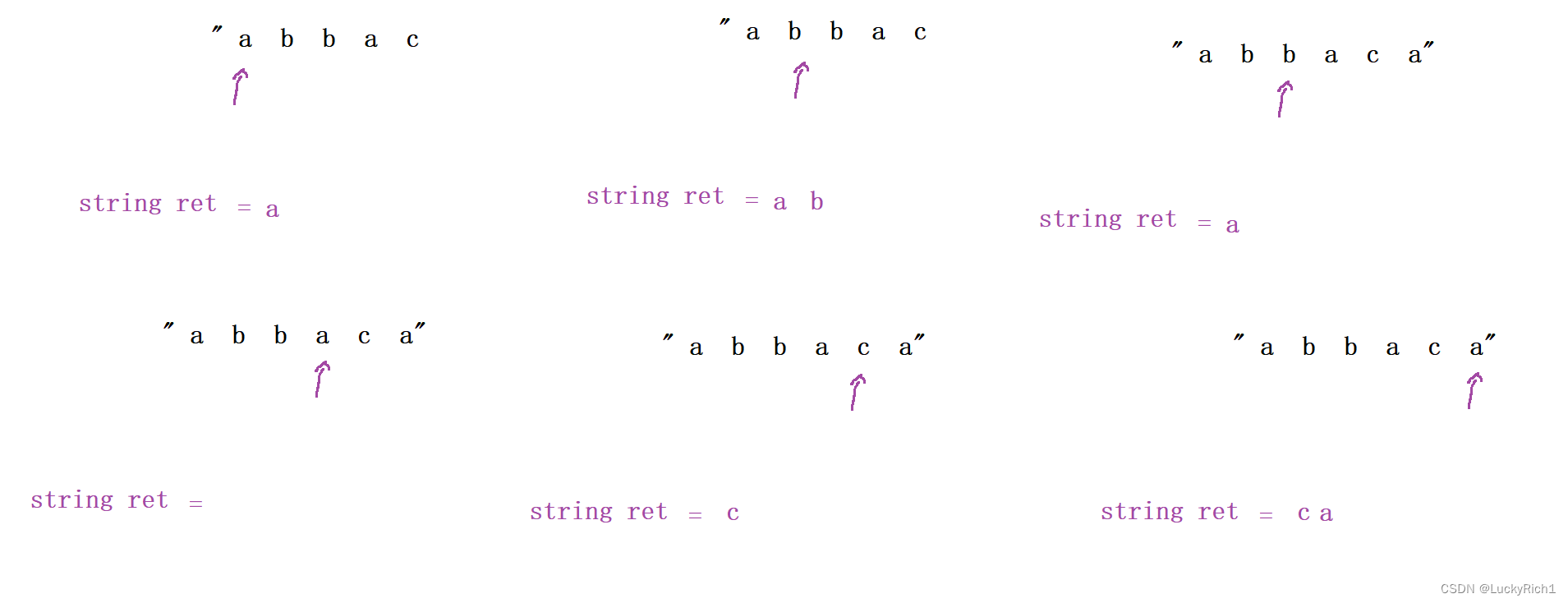
直接用数组就可以模拟这个栈结构,好处就是:模拟完毕之和,数组里面存的就是最终结果。
cpp
class Solution {
public:
string removeDuplicates(string s) {
string ret;// 搞一个数组,模拟栈结构即可
for(int i = 0; i < s.size(); ++i)
if(!ret.empty() && ret.back() == s[i]) //出栈
ret.pop_back();
else
ret += s[i]; // 入栈
return ret;
}
};2.比较含退格的字符串
题目链接: 844. 比较含退格的字符串
题目分析:

遇到 '#' ,就相当于删除前面的元素。
算法原理:
这道题和上面几乎就是一模一样。
解法:利用栈模拟即可
不是 '#' 就进栈,遇到 '#' ,删除前面的元素,如果栈为空就不能删除。两个字符串经过处理最后比较一下即可。
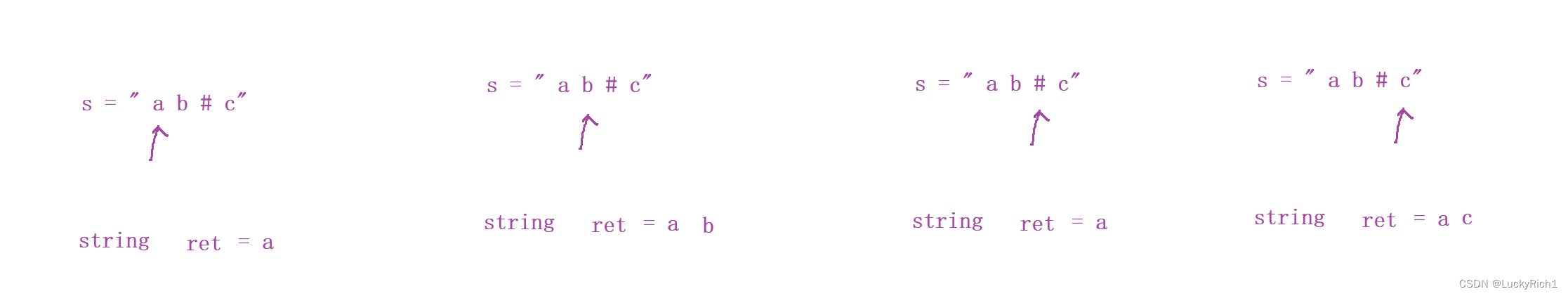
cpp
class Solution {
public:
bool backspaceCompare(string s, string t) {
return changStr(s) == changStr(t);
}
string changStr(string& s)
{
string ret;
for(auto& ch : s)
{
if(ch != '#') ret += ch;
else
{
if(!ret.empty()) ret.pop_back();
}
}
return ret;
}
};3.基本计算器 II
题目链接: 227. 基本计算器 II
题目分析:

s 由整数和算符 ('+', '-', '*', '/') 组成,中间由一些空格隔开。也就说里面是没有括号的,没有括号处理起来还是比较容易的。
算法原理:
这道题虽然是一个基本计数器,但是本质是一种类型的题目,表达式求值,解法是统一的。
解法:利用栈来模拟计算过程
有两种通用的解法:
解法一:中缀表达式转成后缀表达式,然后定义一个操作数栈,扫描后缀表达式,遇到操作数就进栈,遇到运算符就出栈顶两个元素,然后将计算结果在压栈,当后缀表达式结束,栈顶就是我们的运算结果。
中缀表达式转成后缀表达式:
初始化一个栈,用于保存暂时还不能确定顺序的运算符。
从左到右处理各个元素,直到末尾,可能遇到三种情况:
- 遇到操作数,直接加入后缀表达式
- 遇到界限符,遇到 "(" 直接入栈,遇到 ")" 则依次弹出栈内运算符并加入后缀表达式,直到弹出 "(" 为止,注意 "(" 不加入到后缀表达式
- 遇到运算符,依次弹出栈中优先级高于或者等于当前运算符的所有运算符,并加入到后缀表达式,若碰到 "(" 或者栈空则停止,之后再把当前运算符入栈
- 按上述处理完所有字符后,将剩余运算符依次弹出,并加入到后缀表达式
解法二:中缀表达式直接计算,利用两个栈,其中一个栈用来维护操作数,另一个栈用来维护操作符。
- 初始化两个栈,操作数栈和运算符栈
- 扫描到操作数,压入操作实栈
- 扫描到运算符或者界限符,则按照 "中缀转后缀" 相同的逻辑压入运算符栈(期间也会弹出运算符,每当弹出一个运算符时,就需要再弹出两个操作数栈的栈顶元素,并执行相应运算,运算结果再压回操作数栈,最后栈顶元素就是最终运算结果)
不过这道题比较简单,只要 + - * - 四个运算符,并且里面只有正数没有负数,而且还没有括号。所以这道题我们可以用更简单的方法来解决的。我们仅需要一个栈和一个变量就可以了。
接下来模拟一下。
int类型的栈用来保存操作数,op用来标记当前数前面的运算符是什么。
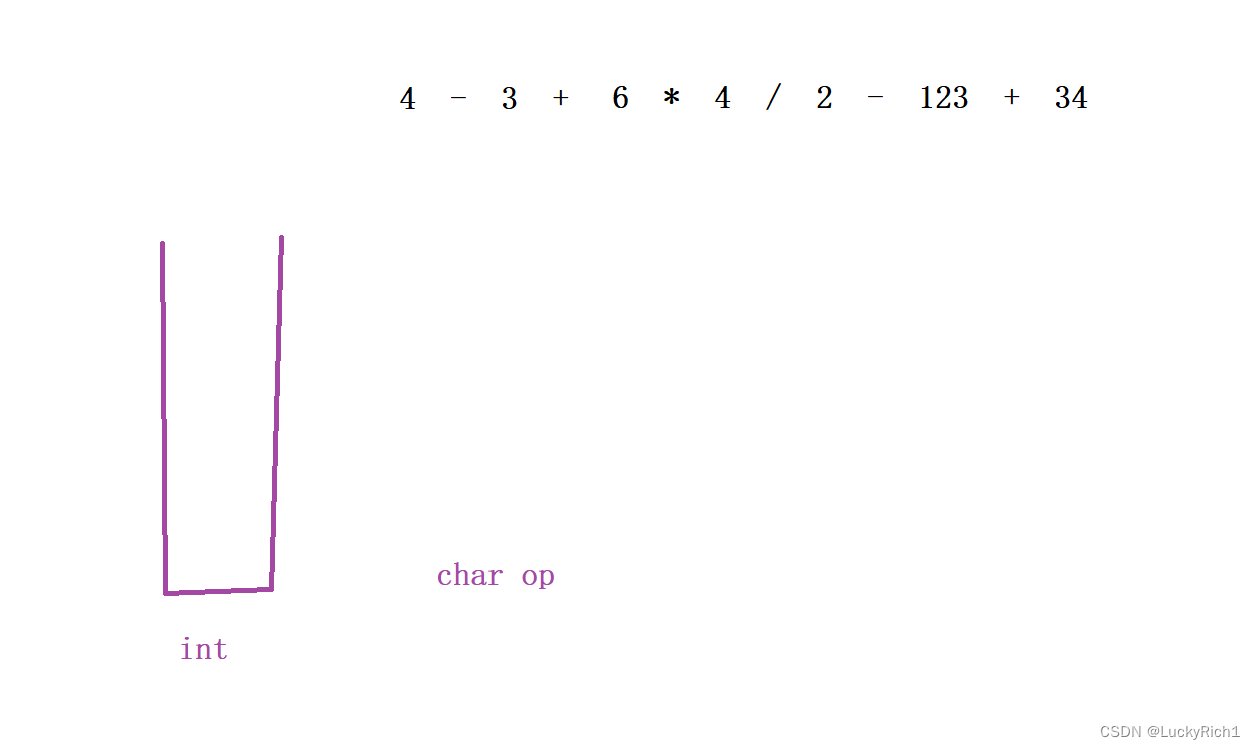
刚开始的时候,把op初始化成一个'+',这样的话第一个数和后面的数处理逻辑是一样的。
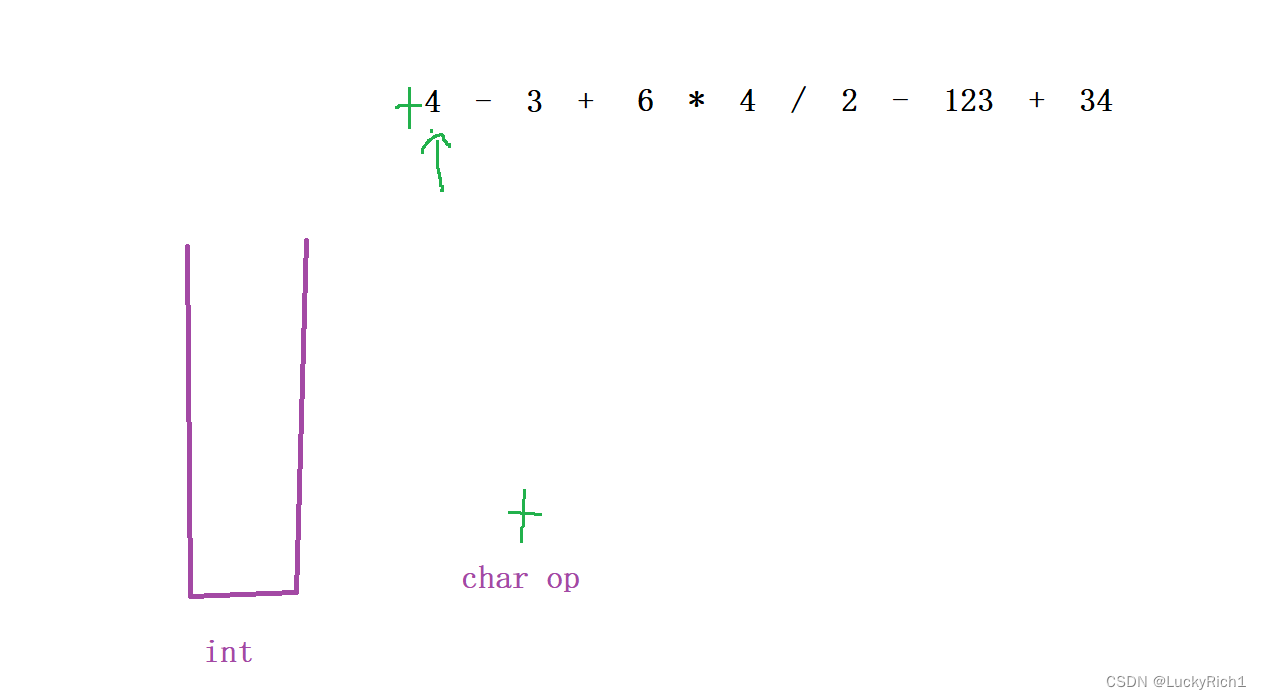
接下来遍历这个字符串,当碰到数字的时候,把数字给提取出来 ,因为这整体是一个字符串。碰到单个数还好说,但是碰到123这种需要把123整体提出来。数字提取出来,然后去看看这个数字前面运算符 ,当是 '+','-' 的时候,这个数字可能还操作不了,因为后面运算符不知道,一旦后面运算符是 '*' ,'/' 这个数字应该先和后面的数先进行运算。所以遇到一个数这个数字前面是 '+','-' 运算符,就把数字丢到栈中。如果是 '+' 数字直接丢到栈中,如果是 '-' 就取这个数字的负数,放入栈中 。这样弄的因为是最后可以把栈里未运算的元素取出来都看成 '+' 运算,直接加就可以了。如果这数字前面是 ' * ' ,'/'。就将这个数字直接和栈顶元素进行相应的运算,因为 ' * ' ,'/' 优先级是最高的在这道题而且这道题并没有括号!
当碰到运算符的时候 直接更新 op。为什么直接更新原因很简单,因为栈里面存的元素如果没有运算的是它前面要么是 '+',要是 '-'。而 ' * ' ,'/' 我们也已经运算过了加入到栈里面了。最后把栈中元素取出来做加法就行了。
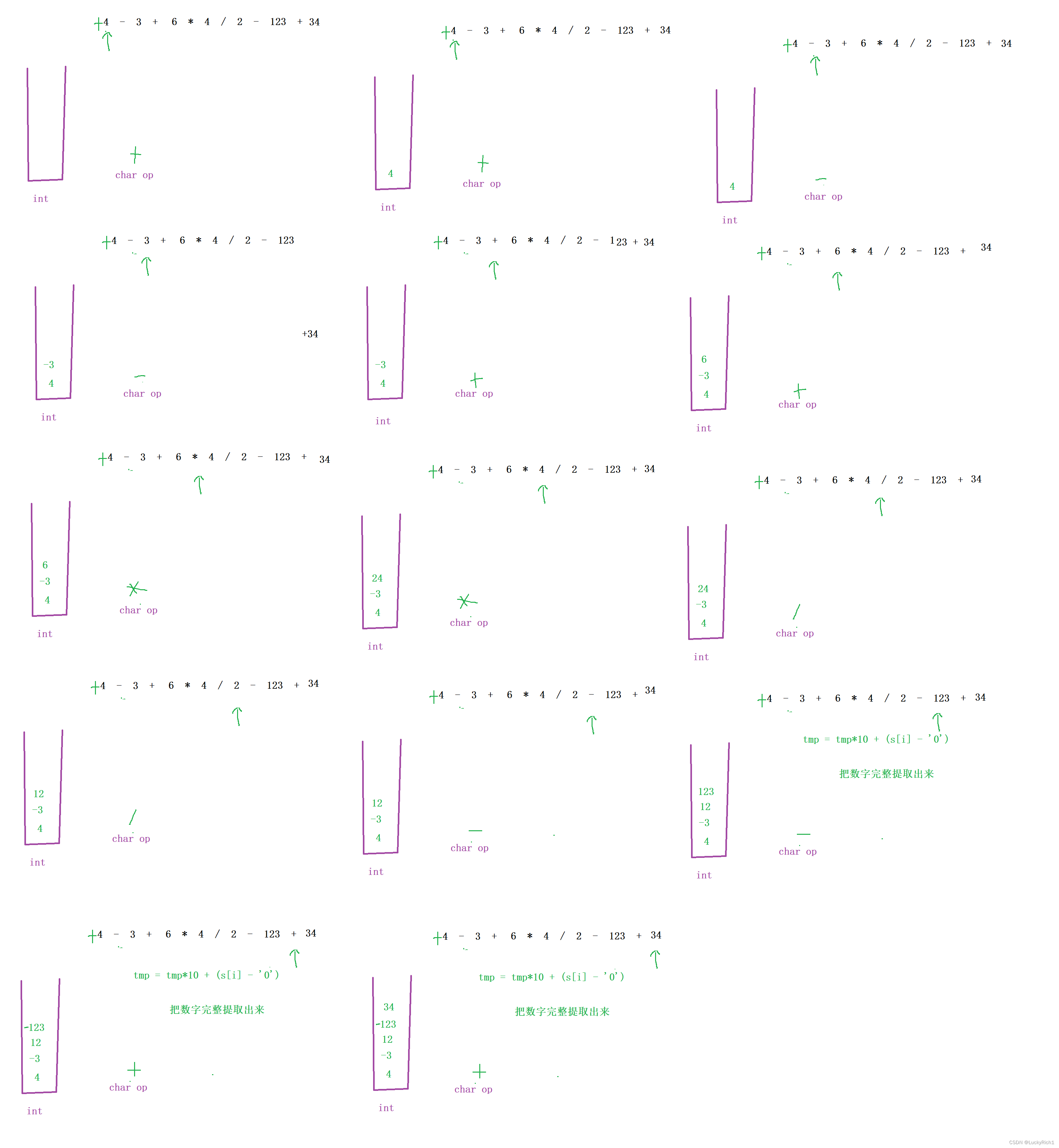
其实这就是一个分情况讨论的过程:
1.遇到操作符:更新操作符 op
2.遇到数字
- 先把数字提取出来, tmp
- 分情况讨论,根据 op 符号
op == '+',tmp直接入栈;
op == '-',-tmp入栈;
op == '*',直接乘到栈顶元素上;
op == '/',直接除到栈顶元素上;
cpp
class Solution {
public:
int calculate(string s) {
vector<int> st;// ⽤数组来模拟栈结构
char op = '+';
int i = 0, n = s.size();
while(i < n)
{
if(s[i] == ' ') ++i;
else if(s[i] >= '0' && s[i] <= '9')
{
// 先把这个数字给提取出来
int tmp = 0;
while(i < n && s[i] >= '0' && s[i] <= '9')
tmp = tmp * 10 + (s[i++] - '0');
if(op == '+') st.push_back(tmp);
else if(op == '-') st.push_back(-tmp);
else if(op == '*') st.back() *= tmp;
else st.back() /= tmp;
}
else
op = s[i++];
}
//取出栈中元素 进行 '+' 运算
int ret = 0;
for(auto e : st) ret += e;
return ret;
}
};4.字符串解码
题目链接: 394. 字符串解码
题目分析:

给一个经过编码的字符串,返回它解码后的字符串。数字后面括号里跟的是要重复几次的字符串。

算法原理:
如果表达式求值里面有加括号,是由内向外计算。有括号先算括号里面的。这道题解码方式也是由内到外的,因此我们可以使用栈。

解法:用栈来模拟
比如说拿到这个1的时候,不知道后面跟的是什么东西,不能贸然就去解码,需要先把后面东西解码之后,在重复。因此这个1需要先保存起来。

当碰到 [ 括号的时候,因为要把后面东西进行解码,因此直接跳过 [ 括号。

碰到字符串a之后,往后走,也要把这个字符串a保存起来,因为a后面要接一堆字符串的,但是需要解码之后才知道后面接的是什么,因此先把字符串a保存起来。

当碰到 ] 括号的时候,前面肯定是有一个 ] 是和我匹配的,所以就可以解码了,拿到前面的最近保存过的字符串bc 和 数字 2 进行解码。

我们是从前往后扫描的 进行保存的,然后碰到 ] 把最近的字符串和数字拿到。这不正好符号栈 后进先出的吗。
当我们分析用栈来解决,接下来就是模拟的过程了。
因为字符串既有数字还有字符串,因此需要一个 "数字栈" 、 " 字符串栈"。
当碰到一个数,先把数提取出来,因为并不知道要让我重复谁,所以先放到 数字栈 中

当遇到 [ , [ 后面一堆东西是需要重复的,但是此时不知道需要重复谁,因此将 [ 后面一小堆字符串提出来先放到 字符串栈 中。

碰到数字和 [ ,同理都是这样的操作

碰到 ] 括号,就可以大胆的解析了,解析的时候仅需把两个栈的栈顶元素提出来,然后解析。接下来重点来了,是把解析后的字符串直接丢到字符串栈里面吗?并不是!因为这一堆东西前面可能还连着字符串,所以是把解析后的字符串放到 字符串栈的栈顶元素后面。

此时右碰到 ] 括号,把两个栈的栈顶元素提出来,然后解析。把解析后的字符串放到 字符串栈的栈顶元素后面。但是此时 字符串栈 是空的 ,会发生越界的情况。因此 字符串栈,初始化给一个 空字符串。 这样在放回去的时候就不会发生越界了。

当碰到单独的字符串之后,把字符串提取出来,因为它前面并没有 [ ,因此可以直接该字符串放到栈顶元素后面,因为这个字符串并不需要重复,直接放在前面解析好的字符串后面就可以了。所以把这个字符串放在栈顶元素后面。

后面的就和前面一样的操作,最终 字符串栈 栈顶元素就是解析后的字符串

总结一下:
细节:字符串栈中,初始化先放入一个空串。
分情况讨论:
- 遇到数字,提取出这个数字,放入 "数字栈" 中
- 遇到 ' [ ',把后面字符串提取出来,放到到 "字符串栈" 中
- 遇到 ' ] ',解析,然后放到 "字符串栈" 栈顶的字符串后面
- 遇到单独的字符,提取出来这个字符串,直接放在"字符串栈" 栈顶的字符串后面
cpp
class Solution {
public:
string decodeString(string s) {
vector<string> strst(1,string());
vector<int> numst;
int i = 0, n = s.size();
while(i < n)
{
if(s[i] >= '0' && s[i] <= '9')
{
int tmp = 0;
while(i < n && s[i] >= '0' && s[i] <= '9')
tmp = tmp * 10 + (s[i++] - '0');
numst.push_back(tmp);
}
else if(s[i] == '[')
{
++i; // 把括号后⾯的字符串提取出来
string str;
while(i < n && isalpha(s[i]))
str += s[i++];
strst.push_back(str);
}
else if(s[i] == ']')
{
string str = strst.back();
strst.pop_back();
int k = numst.back();
numst.pop_back();
while(k--)
strst.back() += str;
++i;//跳过这个右括号
}
else
{
string str;
while(i < n && isalpha(s[i]))
str += s[i++];
strst.back() += str;
}
}
return strst.back();
}
};5.验证栈序列
题目链接: 946. 验证栈序列
题目描述:

给一个入栈顺序和出栈顺序,看是否匹配。
算法原理:
解法:借助栈模拟即可
让进栈元素一直进栈,进栈之后让栈顶元素和出栈元素比较是否相等,相等且栈不为空就一直出栈,不相等继续进栈。当进栈元素都进栈之后,如果栈不为空 或者 出栈元素还没有完,就不匹配,否则匹配。

- 让元素一直进栈
- 进栈的同时,判断是否出栈即可
- 当所有元素进栈完毕之后,判断 i 是否已经遍历完毕 或者 判断栈是否为空即可。
cpp
class Solution {
public:
bool validateStackSequences(vector<int>& pushed, vector<int>& popped) {
stack<int> st;
int i = 0;
for(auto &e : pushed)
{
st.push(e);
while(!st.empty() && popped[i] == st.top())
{
st.pop();
++i;
}
}
if(!st.empty()) return false;
return true;
}
};