萝卜快跑涨价
距离我们上次谈 萝卜快跑 不足半月,萝卜快跑迎来了不少"反转"。
先是被曝远程后台有人操控,真实日成本超 400:

最近还被不少网友吐槽:萝卜快跑涨价了,如今价格和网约车持平。
据不少博主实测,最近武汉萝卜快跑的打车成功率,低得离谱,不足 30%,基本上叫车 3~4 次,才能成功 1 次。
叫车不好叫,价格还贵。
之前的萝卜快跑,叠加优惠等福利,可以做到几毛钱一公里,如今的价格基本上都在 1.5 元以上,和网约车基本持平。
知道「打车自由」迟早要没,但没想到没得这么快 🤣
首先,萝卜快跑的定价权是在百度手上的,萝卜快跑如今选择涨价,和网约车保持相当的水准。
我觉得和前段时间萝卜快跑的舆论热度超预期是密切相关的,而且在当前时间节点选择涨价到网约车水平,我觉得是非常聪明的。
先别急着反驳,我当然也是希望打车自由的时间能长一点。
但如果从百度(甚至是社会交通运输行业)的角度出发,萝卜快跑还是一个尚未全国铺开的产品,甚至还是一个内测产品,同时也代表了一个未来很有前景的行业,现如今却落入"抢人类饭碗"的社会问题舆论中,很容易就会导致整个行业被扼杀。
尤其是被曝日成本超过 400 之后,如果萝卜快跑再继续保持补贴低价,舆论只会更加汹涌。
从现在的环境分析,萝卜快跑的流量已经上来了,此时选择涨价到正常水平,可以进一步平衡订单的供求关系,又可以让舆论冷却,还能达成当时补贴是「为了拿到更多真实数据」的目的,是最符合经济原则的做法。
...
回归主题。
来一道和「小红书,社招二面」相关的算法原题。
题目描述
平台:LeetCode
题号:1206
不使用任何库函数,设计一个跳表。
跳表 是在 时间内完成增加、删除、搜索操作的数据结构。
跳表相比于树堆与红黑树,其功能与性能相当,并且跳表的代码长度相较下更短,其设计思想与链表相似。
例如,一个跳表包含 [30, 40, 50, 60, 70, 90],然后增加 80、45 到跳表中,以下图的方式操作:
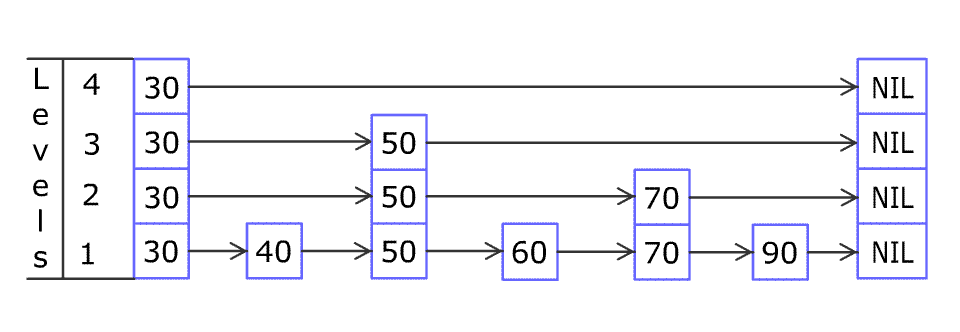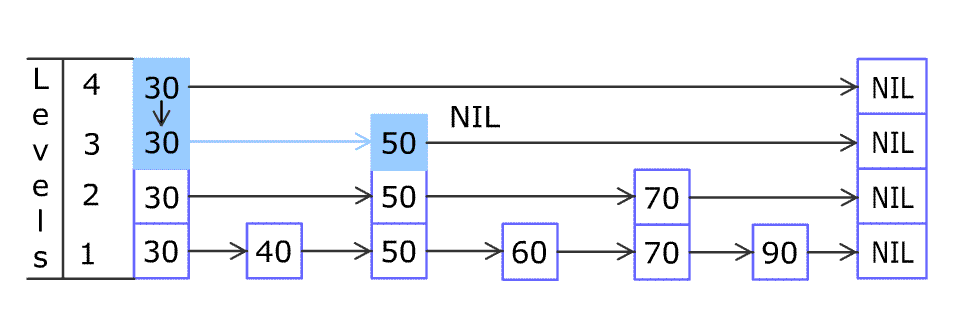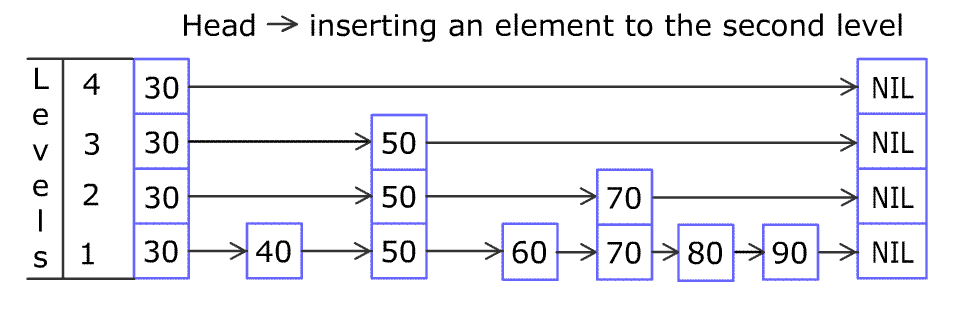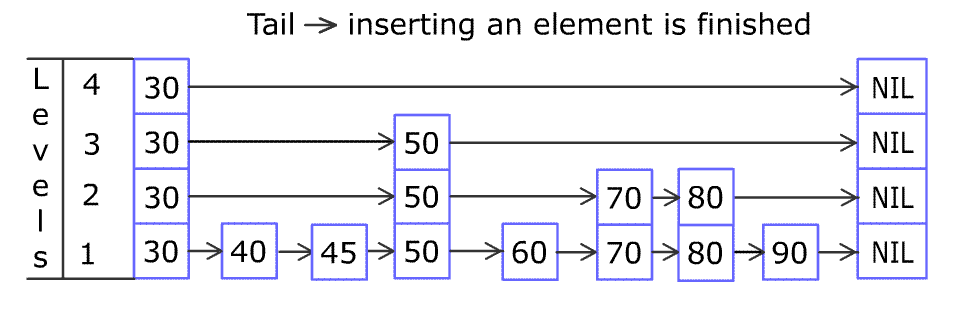
跳表中有很多层,每一层是一个短的链表。在第一层的作用下,增加、删除和搜索操作的时间复杂度不超过 。
跳表的每一个操作的平均时间复杂度是 ,空间复杂度是 。
在本题中,你的设计应该要包含这些函数:
bool search(int target): 返回target是否存在于跳表中。void add(int num): 插入一个元素到跳表。bool erase(int num): 在跳表中删除一个值,如果num不存在,直接返回false. 如果存在多个num,删除其中任意一个即可。
注意,跳表中可能存在多个相同的值,你的代码需要处理这种情况。
示例 1:
输入
["Skiplist", "add", "add", "add", "search", "add", "search", "erase", "erase", "search"]
[[], [1], [2], [3], [0], [4], [1], [0], [1], [1]]
输出
[null, null, null, null, false, null, true, false, true, false]
解释
Skiplist skiplist = new Skiplist();
skiplist.add(1);
skiplist.add(2);
skiplist.add(3);
skiplist.search(0); // 返回 false
skiplist.add(4);
skiplist.search(1); // 返回 true
skiplist.erase(0); // 返回 false,0 不在跳表中
skiplist.erase(1); // 返回 true
skiplist.search(1); // 返回 false,1 已被擦除提示:
- 调用
search,add,erase操作次数不大于
数据结构
对于单链表而言,所有的操作(增删改查)都遵循「先查找,再操作」的步骤,这导致在单链表上所有操作复杂度均为 (瓶颈在于查找过程)。
跳表相对于单链表,则是通过引入「多层」链表来优化查找过程,其中每层链表均是「有序」链表:
- 对于单链表的
Node设计而言,我们只需存储对应的节点值val,以及当前节点的下一节点的指针ne即可(ne为一指针变量) - 对于跳表来说,除了存储对应的节点值
val以外,我们需要存储当前节点在「每一层」的下一节点指针ne(ne为指针数组)
跳表的 level 编号从下往上递增,最下层的链表为元素最全的有序单链表,而查找过程则是按照 level 从上往下进行。
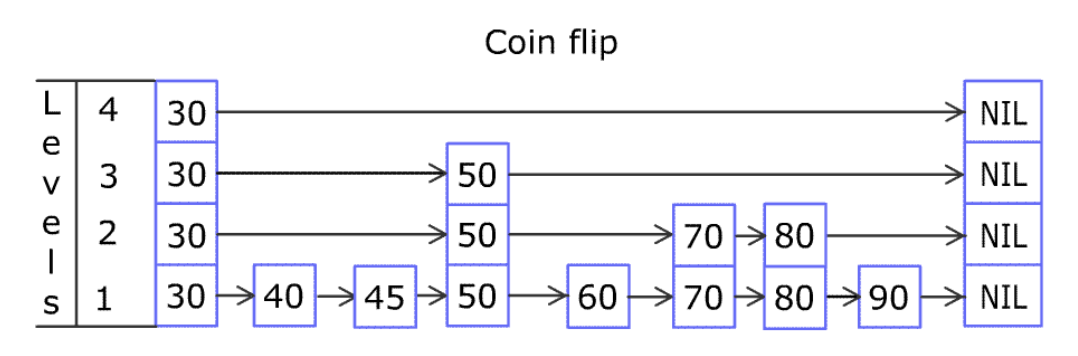
操作次数的数据范围为 ,因此设计最大的 level 为 即可确保复杂度,但由于操作次数 不可能全是 add 操作,因此这里直接取 level 为 10。
同时为了简化,建立一个哨兵节点 he,哨兵值的值应当足够小(根据数据范围,设定为 即可),所有的操作(假设当前操作的传入值为 t),先进行统一化的查找:「查找出每一层比 t 严格小的最后一个节点,将其存成 ns 数组。即 为 层严格比 小的最后一个节点。」
再根据不同的操作进行下一步动作:
search操作:由于最后一层必然是元素最全的单链表,因此可以直接访问ns[0].ne[0]即是所有元素中满足大于等于t的第一个元素,通过判断其值与传入值t的大小关系来决定结果;add操作:由于最后一层必然是元素最全的单链表,因此我们「从下往上」进行插入,最底下一层必然要插入,然后以一半的概率往上传递;erase操作:与add操作互逆,按照「从下往上」的顺序进行删除。需要注意的是,由于相同的值在跳表中可能存在多个,因此我们在「从下往上」删除过程中需要判断待删除的元素与ns[0].ne[0]是否为同一元素(即要判断地址是否相同,而不是值相同)。
Java 代码:
class Skiplist {
int level = 10;
class Node {
int val;
Node[] ne = new Node[level];
Node (int _val) {
val = _val;
}
}
Random random = new Random();
Node he = new Node(-1);
void find(int t, Node[] ns) {
Node cur = he;
for (int i = level - 1; i >= 0; i--) {
while (cur.ne[i] != null && cur.ne[i].val < t) cur = cur.ne[i];
ns[i] = cur;
}
}
public boolean search(int t) {
Node[] ns = new Node[level];
find(t, ns);
return ns[0].ne[0] != null && ns[0].ne[0].val == t;
}
public void add(int t) {
Node[] ns = new Node[level];
find(t, ns);
Node node = new Node(t);
for (int i = 0; i < level; i++) {
node.ne[i] = ns[i].ne[i];
ns[i].ne[i] = node;
if (random.nextInt(2) == 0) break;
}
}
public boolean erase(int t) {
Node[] ns = new Node[level];
find(t, ns);
Node node = ns[0].ne[0];
if (node == null || node.val != t) return false;
for (int i = 0; i < level && ns[i].ne[i] == node; i++) ns[i].ne[i] = ns[i].ne[i].ne[i];
return true;
}
}Python 代码:
class Skiplist:
def __init__(self, level=10):
self.level = level
class Node:
def __init__(self, val):
self.val = val
self.ne = [None] * level
self.Node = Node
self.he = Node(-1)
def find(self, t, ns):
cur = self.he
for i in range(self.level - 1, -1, -1):
while cur.ne[i] is not None and cur.ne[i].val < t:
cur = cur.ne[i]
ns[i] = cur
def search(self, t):
ns = [None] * self.level
self.find(t, ns)
return ns[0].ne[0] is not None and ns[0].ne[0].val == t
def add(self, t):
ns = [None] * self.level
self.find(t, ns)
node = self.Node(t)
for i in range(self.level):
node.ne[i] = ns[i].ne[i]
ns[i].ne[i] = node
if random.randint(0, 1) == 0:
break
def erase(self, t):
ns = [None] * self.level
self.find(t, ns)
node = ns[0].ne[0]
if node is None or node.val != t:
return False
for i in range(self.level):
if ns[i].ne[i] == node:
ns[i].ne[i] = ns[i].ne[i].ne[i]
return TrueTypeScript 代码:
const level: number = 10
class TNode {
val: number
ne: TNode[] = new Array<TNode>(level)
constructor(_val: number) {
this.val = _val
}
}
class Skiplist {
he: TNode = new TNode(-1)
find(t: number, ns: TNode[]): void {
let cur = this.he
for (let i = level - 1; i >= 0; i--) {
while (cur.ne[i] != null && cur.ne[i].val < t) cur = cur.ne[i]
ns[i] = cur
}
}
search(t: number): boolean {
let ns: TNode[] = new Array<TNode>(level)
this.find(t, ns)
return ns[0].ne[0] != null && ns[0].ne[0].val == t
}
add(t: number): void {
let ns: TNode[] = new Array<TNode>(level)
this.find(t, ns)
const node = new TNode(t)
for (let i = 0; i < level; i++) {
node.ne[i] = ns[i].ne[i]
ns[i].ne[i] = node
if (Math.round(Math.random()) == 0) break
}
}
erase(t: number): boolean {
let ns: TNode[] = new Array<TNode>(level)
this.find(t, ns)
const node = ns[0].ne[0]
if (node == null || node.val != t) return false
for (let i = 0; i < level && ns[i].ne[i] == node; i++) ns[i].ne[i] = ns[i].ne[i].ne[i]
return true
}
}- 时间复杂度:所有操作的复杂度瓶颈在于
find查找,find查找期望复杂度为 - 空间复杂度:
最后
巨划算的 LeetCode 会员优惠通道目前仍可用 ~
使用福利优惠通道 leetcode.cn/premium/?promoChannel=acoier ,年度会员 有效期额外增加两个月 ,季度会员 有效期额外增加两周,更有超大额专属 🧧 和实物 🎁 福利每月发放。
我是宫水三叶,每天都会分享算法知识 ,并和大家聊聊近期的所见所闻。
欢迎关注,明天见。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉