
照片由Edge2Edge Media在Unsplash上拍摄
一、介绍
在概率的许多应用中,不可能直接观察实验的结果;而是观察与结果相关的事件。因此,条件概率模型对于考虑和利用从观察到的事件中获得的信息至关重要。此外,条件概率模型与贝叶斯定理非常相关。在这篇博客中,我将介绍条件概率模型的基础知识,并使用参考文献 [1] 解答一些测验以熟悉该概念。
概念表
二、条件概率
条件概率听起来很吓人,但它仅仅是指在事件 B 下事件 A 发生的概率的比例。理论上,当我们有样本空间 S 时,条件概率可以描述为在事件 B 已经发生的条件下,事件 A 发生的概率。

条件概率可视化
当我们改变边际概率值时,条件概率会如何变化?可视化如下图所示。从图中可以看出,联合概率越大,A占B的比例就越大。

当边际概率改变时,条件概率如何变化?
条件概率定理适用于离散型随机变量和连续型随机变量这两类随机变量。当我们将样本空间定义为 S,且事件 B ⊂ S 时,离散型随机变量和连续型随机变量的条件概率描述为:

两个随机变量的条件概率公式
从上面的方程中,我们可以推导出边际概率的公式。
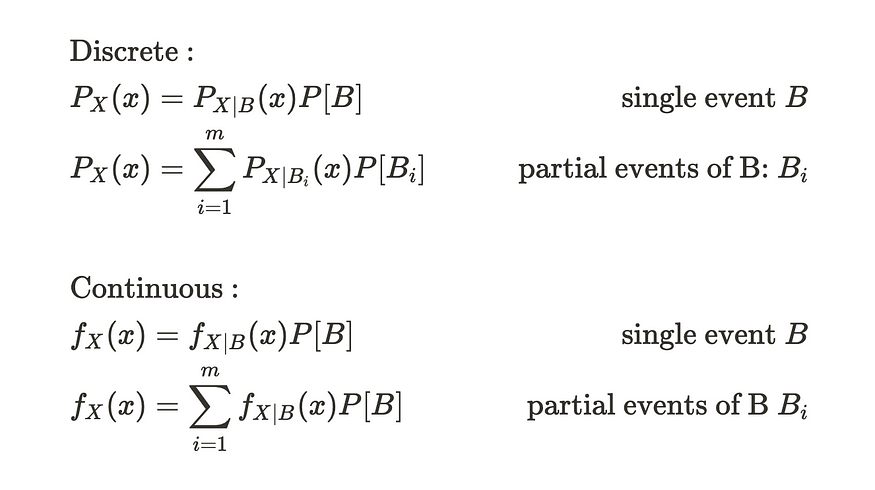
边际概率公式
边际概率是单个事件发生的概率。上面的公式意味着,如果我们知道与单个事件相关的所有其他事件以及它占其他事件的比例,我们就可以知道单个事件的概率。接下来,让我们解决以下问题来检查我们对条件概率的理解。

测验 1.1

测验 1.1 答案

测验 1.2

测验 1.2 答案
三、条件期望值和条件方差
条件期望值和条件方差也是重要的概念。获得具有特定条件的统计数据可以帮助我们深入了解给定的数据。在本节中,我们将深入研究条件期望值和方差,以从数学上理解它们。
3.1 条件期望值
条件期望值与非条件概率的期望值类似,它用条件概率代替期望值中的非条件概率部分。

条件期望值定理
给定分区 Bᵢ 的条件概率模型,我们可以根据条件预期值 E[X|Bᵢ] 计算预期值 E[X]。
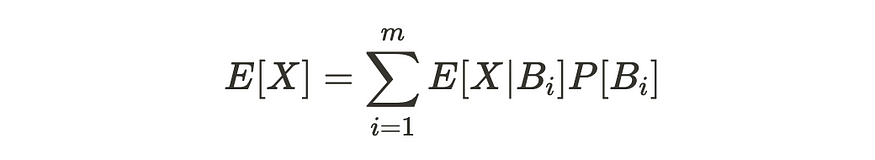
上述公式类似于事件有分区时条件概率与边际概率的关系。如果我们将所有分区事件的概率与它们的条件期望值相加,它就变成了期望值。我们可以得出这个公式如下:

条件概率与边际概率关系的推导
3.2 条件方差
条件方差也与非条件概率的方差类似。条件标准差可以描述为:
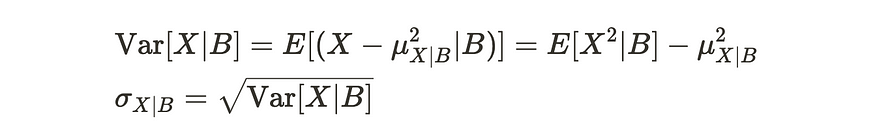
条件方差定理
您可以得出条件方差公式如下:
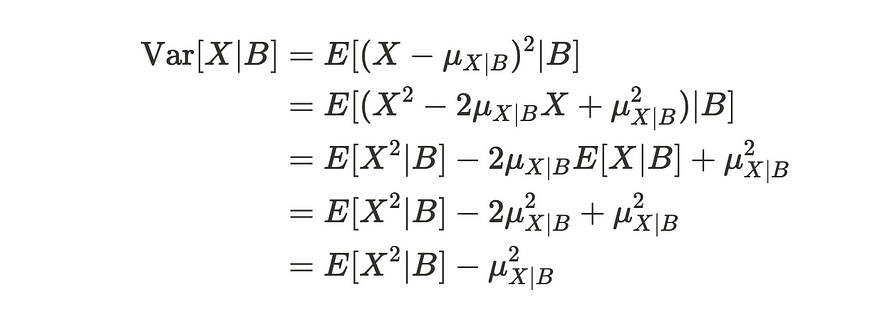
条件方差的推导
为了熟悉这些概念,让我们解决下面的问题。

测验 2.1
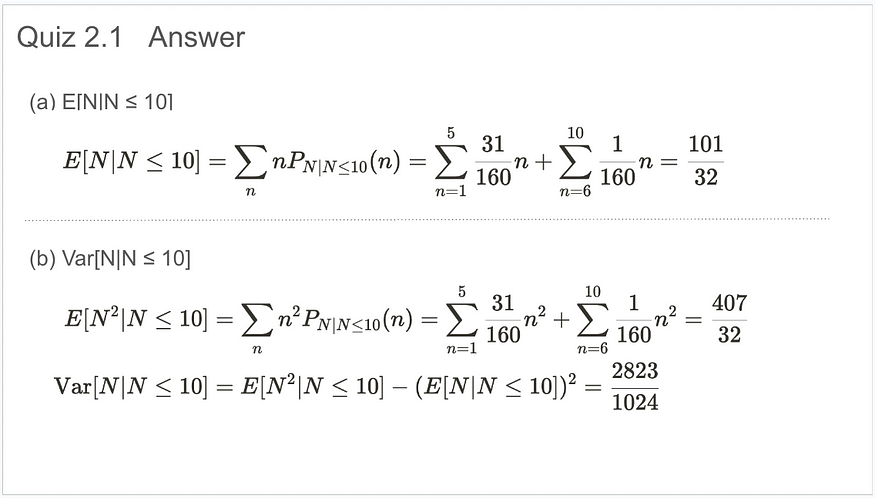
测验 2.1 答案

测验 2.2
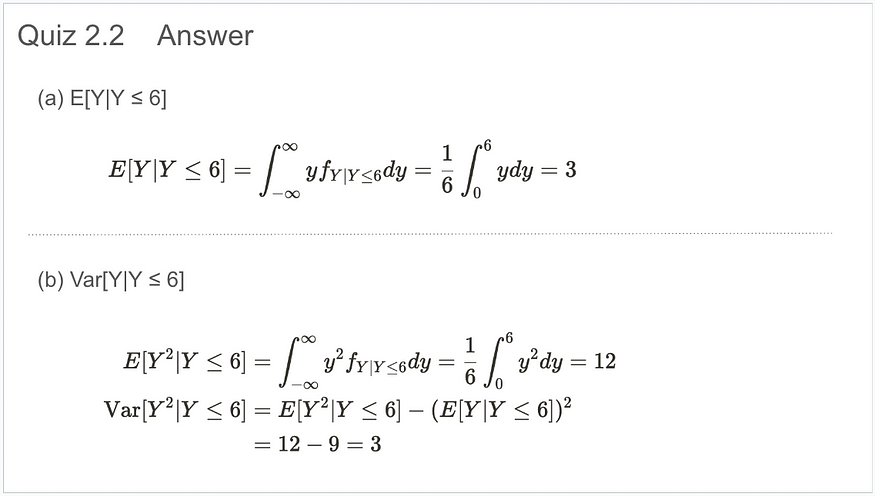
测验 2.2 答案
四、 回顾条件概率的练习
在最后的部分,我将使用书中[1]的一些测验来理解条件概率和相关理论的概念。

测验 3.1

测验 3.1 答案 1

测验 3.1 答案 2

测验 3.2

测验 3.2 答案 1

测验 3.2 答案 2

测验 3.3

测验 3.3 答案 1

测验 3.3 答案 2
在这篇博客中,我们讨论了条件概率定理。这个概念对于理解贝叶斯定理和应用机器学习(例如自然语言处理)至关重要。感谢您的阅读!