小孔成像
用一个带有小孔的板遮挡在墙体与物之间,墙体上就会形成物的倒影,我们把这样的现象叫小孔成像。
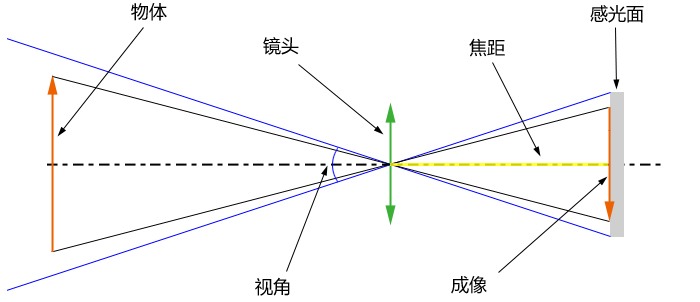
用一个带有小孔的板遮挡在墙体与物之间,墙体上就会形成物的倒影,我们把这样的现象叫小孔成像。前后移动中间的板,墙体上像的大小也会随之发生变化,这种现象说明了光沿直线传播的性质。
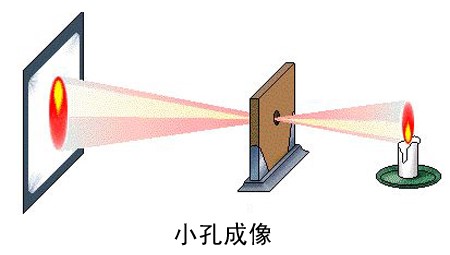
在照相机被发明之前,人们就已经开始利用"小孔成像"原理制造各类光学成像装置,这种装置被称为"Camera obscura(暗箱)"。 19世纪上半叶,人们终于找到了固定保存暗箱中投影面上光学图像的方法与介质,照相机工业由此发展,因此Camera obscura被认为是照相机的祖先;而"Camera"则成了照相机的英文名称。
1839 年法国画家达盖尔根据小孔成像的原理发明了被称为"西洋镜"的世界第一台照相机。 不过当时的相机令现代人无法想象,暗箱大得像个小房子,拍摄时间至少三十分钟,以至于不得不将被摄的人头部固定在事先预制好的卡箍里,而且得到的只是一张笨重的铜版正像。 当时有报社记者评述:"就像在马路上拿着一面镜子,周围的景物极细地反映出来,然后把镜子带回家。"

现代照相机和摄影机也是利用了小孔成像的原理------镜头是小孔(大多数安装凸透镜以保证光线成像距离),景物通过小孔进入暗室,影像被一些特殊的化学物质(如显影剂等)留在胶片上。 数码相机、摄影机等则是将影像通过感光元件转换为数字信号(数码格式)存储在存储卡内。
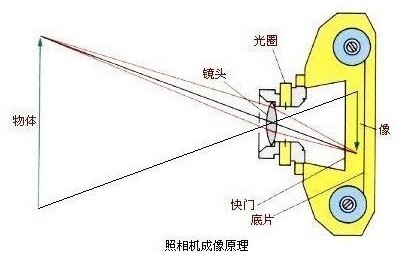
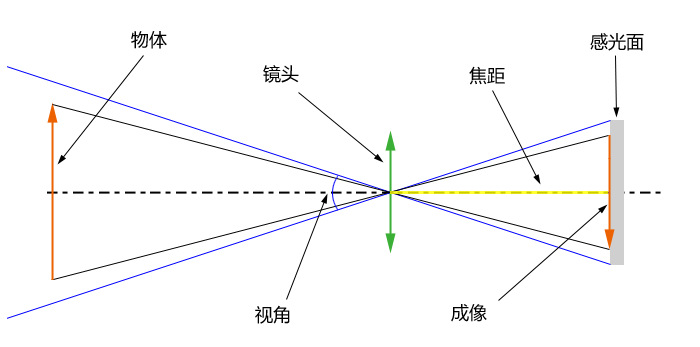
其实,人类的视觉系统也是小孔成像的原理。只不过视觉系统的复杂度是相机系统的成千上万倍。
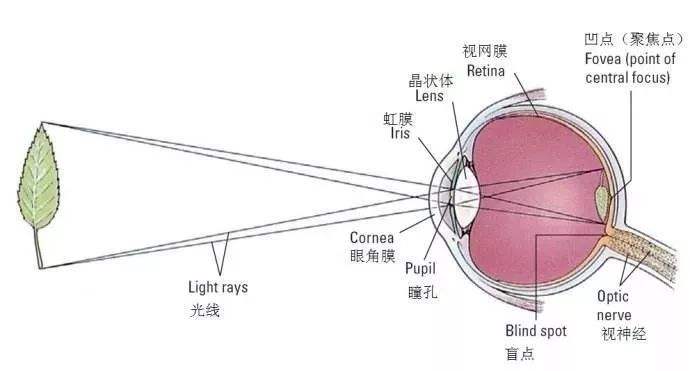
小孔成像模型

上图是最原汁原味的小孔成像原理图,它描述的是三维空间中的点到图像平面(image plane)上的投影。
在实际的实现和应用中,为了表达的方便,通常会将图像平面放在小孔和三维场景之间。如下图所示:



这里介绍几个概念:
- 光轴:像极坐标系的Z轴
- 光心:光轴中心点,即上图中的O点
- 主点:光轴与图像平面的交点Principal Point
- 焦距:光心到图像平面的距离Focal Length
四个坐标系
为了数学表达的方便,通常以光心为原点,建立一个图像坐标系。下图详细的描述了这些关系。

世界坐标系: O w − X w Y w Z w O_w−X_wY_wZ_w Ow−XwYwZw 单位m
世界坐标系(world coordinate),也称为测量坐标系,是一个三维直角坐标系,以其为基准可以描述相机和待测物体的空间位置。世界坐标系的位置可以根据实际情况自由确定。
相机坐标系: O c − X c Y c Z c O_c−X_cY_cZ_c Oc−XcYcZc 单位m
相机坐标系(camera coordinate),也是一个三维直角坐标系,原点位于镜头光心处,x、y轴分别与相面的两边平行,z轴为镜头光轴,与像平面垂直。
像素坐标系: O u v − u v O_{uv}−uv Ouv−uv 单位像素pixel(整数)
像素坐标系(pixel coordinate),二维直角坐标系,反映了相机CCD/CMOS芯片中像素的排列情况。原点ouv位于图像的左上角,u轴、v轴分别于像面的两边平行。像素坐标系中坐标轴的单位是像素pixel(整数)
几乎所有的图像,像素坐标都如下图所示:

即:像素原点在图像的左上角,横坐标值表示列数c,通常以u表示;纵坐标值表示行数r,通常以v表示。
图像坐标系: O x y − x y O_{xy}−xy Oxy−xy 单位mm
图像坐标系(image coordinate),由于像素坐标系不利于坐标变换,因此需要建立图像坐标系oxy,其坐标轴的单位为毫米(mm),原点是相机光轴与相面的交点(称为主点Principal Point),即图像的中心点,x轴、y轴分别与u轴、v轴平行。故两个坐标系实际是平移关系,即可以通过平移就可得到。
如下图:(u0,v0) 为图像坐标系中心O在像素坐标系下的位置表示。

点在各个坐标系的表达:
