【数据结构】-----二叉搜索树(C++)

suri ..2024-08-09 8:43

目录

前言

一、是什么

​编辑

二、实现

Ⅰ、结点类

Ⅱ、结构及基本接口实现

​编辑

①插入

②查找

③删除(重难点)

情况一：待删除结点为叶子结点(无孩子)

情况二：待删除结点存在一个孩子结点(可能左/右)

情况三：待删除结点存在两个孩子

④中序遍历

⑤构造函数

⑥拷贝构造

⑦赋值重载

⑧析构函数

Ⅲ、完整实现代码

三、应用

1.K模型

[2.KV 模型](#2.KV 模型)

3.K简单改造KV模型

四、性能分析

前言

前面浅谈了二叉树，但是单谈没啥太大意义，来看点不一样的。。二叉搜索

一、是什么

二叉搜索树也称二叉排序树，它具有以下性质：

  • 若左 子树不为空，则左子树上所有结点的值都小于根结点的值
  • 若右 子树不为空，则右子树上所有结点的值都大于根结点的值
  • 左右子树也分别为二叉搜索树
  • 可以是空树
  • 中序遍历的结果是有序的！

形如：

二、实现

Ⅰ、结点类

cpp 复制代码 
template<class K>
class BSTreeNode
{
public:
	BSTreeNode<K*> _left;
	BSTreeNode<K*> _right;
	K _key;

	BSTreeNode(const K& key)
		:_left(nullptr)
		,_right(nullptr)
		,_key(key)
	{}
};

结点一般对外开放，所以设置为公有，当然你也可以直接用struct关键字！

Ⅱ、结构及基本接口实现

①插入

整体操作：

1.判断是否为空树，为空可直接插入！

2.不为空，找到合适的位置插入，按照二叉搜索树的性质，比较待插入结点和根结点的值，若 新结点<根结点，就插入左子树，反之插入右子树，循环即可！

细节：需要记录父亲结点的位置！

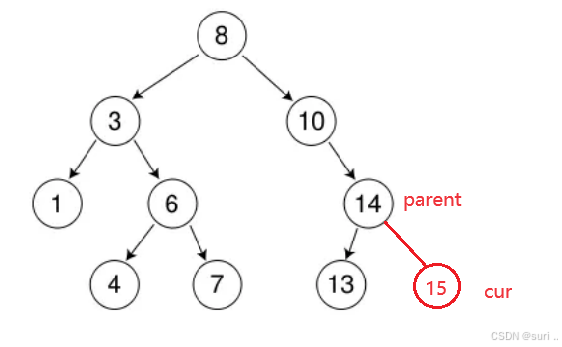
cpp 复制代码 
	bool Insert(const K& key)
	{
		if (_root == nullptr)
		{
			_root = new Node(key);
			return true;
		}

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			//小于找左边
			if (key < cur->_key)
			{
				parent = cur;
				cur = cur->_left;
			}
			//大于找右边
			else if (key > cur->_key)
			{
				parent = cur;
				cur = cur->_right;
			}
			//不允许数据冗余,相等不插入
			else
			{
				return false;
			}
		}
		cur = new Node(key);
		if (key < parent->_key)
		{
			//放左边
			parent->_left = cur;
		}
		else
		{
			//放右边
			parent->_right = cur;
		}
		return true;
	}

②查找

简单的遍历操作，大于找右边，小于找左边

cpp 复制代码 
	bool Find(const K& key)
	{
		if (_root == nullptr)
			return false;

		Node* cur = _root;
		while (cur)
		{
			if (key < cur->_key)
			{
				cur = cur->_left;
			}
			else if (key > cur->_key)
			{
				cur = cur->_right;
			}
			//相等就找到
			else
				return true;
		}
		return false;
	}

③删除(重难点)

首先需要找元素是否存在，不存在就直接返回即可。若存在，则需要分三种情况

情况一：待删除结点为叶子结点(无孩子)

这种情况可直接删除，具体方法：让父亲结点指向空即可，若删除结点在左，那父亲左指向空，反之，父亲右指向空。

例如：

情况二：待删除结点存在一个孩子结点(可能左/右)

**这种情况的本质就是让待删除结点孩子顶替待删除结点位置即可，**做法就是待删除结点的父亲指向待删除结点的孩子，在删除。

还需要注意一个特殊情节，如果这棵二叉搜索树如下：

综上代码具体实现如下：

cpp 复制代码 
//左边空，即存在右子树，父亲指向右
if (cur->_left == nullptr)
{
        //单分支
	    if (cur == _root){
		    _root = cur->_right;		
	    }
	    else{
			//待删除结点在左
			if (cur == parent->_left){
				parent->_left = cur->_right;//父亲左指向右
			}
			else
				parent->_right = cur->_right;//父亲右指向左
		}
		delete cur;
}

//右为空，即存在左子树,父亲指向左子树
else if (cur->_right == nullptr)
{
		//单分支
		if (cur == _root){
		    _root = cur->_left;
        }
		else{
		    //待删除结点在左
		    if (cur == parent->_left){
				parent->_left = cur->_left;//父亲左指向左
			}
			else
				parent->_right = cur->_left;//父亲右指向右
		}
				delete cur;
}

实际上这种情况也包含了情况一，无孩子结点，即既没有左，也没有右

情况三：待删除结点存在两个孩子

这种情况采用**替换法，**就是用左子树的最大结点/或者右子树的最小结点去替换，交换后，在删除。

替换后：

代码实现如下：

以找右子树的最小值为例，右子树的最小值就是在右子树的最左边。

cpp 复制代码 
else
{
	Node* RightMinp = cur;
	Node* RightMin = cur->_right;
	//找右子树的最左边
	while (RightMin->_left)
	{
		RightMinp = RightMin;
		RightMin = RightMin->_left;
	}
	swap(RightMin->_key, cur->_key);//交换

	//左为空，存在右子树，父亲指向右
	if (RightMin = RightMinp->_left)
    {
		RightMinp->_left = RightMin->_right;
	}
	else
	{
		RightMinp->_right = RightMin->_right;
	}
	delete RightMin;
}

④中序遍历

这里为了对外不能访问私有的成员变量，所以采用以下写法：

cpp 复制代码 
public:
    void Inoder()
    {
	    _Inoder(_root);
	    cout << endl;
    }
private:
    Node *_root;//私有成员变量
	void _Inoder(Node* root)
	{
		if (root == nullptr)
			return;
		_Inoder(root->_left);
		cout << root->_key << " ";
		_Inoder(root->_right);
	}

⑤构造函数

cpp 复制代码 
BSTree()
    :_root(nullptr)
{}

⑥拷贝构造

和构造二叉树类似，先构造根结点，在分别构造左右子树！

cpp 复制代码 
	Node* Copy(Node* root)
	{
		if (root == nullptr)
			return nullptr;
		Node* newroot = new Node(root->_key);//拷贝根
		newroot->_left = Copy(root->_left);//拷贝左
		newroot->_right = Copy(root->_right);//拷贝右
		return newroot;
	}


	BSTree(const BSTree<K>& t)
	{
		_root = Copy(t._root);
	}

⑦赋值重载

cpp 复制代码 
//现代写法，复用拷贝构造
BSTree<K>& operator=(BSTree<K> t)
{
	swap(_root, t._root);
	return *this;
}

⑧析构函数

这里要先分别清理左右，最后在清理根！

cpp 复制代码 
void Destoy(Node* root)
{
	if (root == nullptr)
		return;
	Destoy(root->_left);
	Destoy(root->_right);
	delete root;
}

~BSTree()
{
	Destoy(_root);
	_root = nullptr;//要置空
}

Ⅲ、完整实现代码

cpp 复制代码 
template<class K>
class BSTreeNode
{
public:
	BSTreeNode<K>* _left;
	BSTreeNode<K>* _right;
	K _key;

	BSTreeNode(const K& key)
		:_left(nullptr)
		,_right(nullptr)
		,_key(key)
	{}
};

//二叉树结构
template<class K>
class BSTree
{
	typedef BSTreeNode<K> Node;
public:
	BSTree()
		:_root(nullptr)
	{}
	BSTree(const BSTree<K>& t)
	{
		_root = Copy(t._root);
	}
	BSTree<K>& operator=(BSTree<K> t)
	{
		swap(_root, t._root);
		return *this;
	}
	~BSTree()
	{
		Destoy(_root);
		_root = nullptr;
	}

	bool Insert(const K& key)
	{
		if (_root == nullptr)
		{
			_root = new Node(key);
			return true;
		}

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			//小于找左边
			if (key < cur->_key)
			{
				parent = cur;
				cur = cur->_left;
			}
			//大于找右边
			else if (key > cur->_key)
			{
				parent = cur;
				cur = cur->_right;
			}
			//不允许数据冗余,相等不插入
			else
			{
				return false;
			}
		}
		cur = new Node(key);
		if (key < parent->_key)
		{
			//放左边
			parent->_left = cur;
		}
		else
		{
			//放右边
			parent->_right = cur;
		}
		return true;
	}
	bool Find(const K& key)
	{
		if (_root == nullptr)
			return false;

		Node* cur = _root;
		while (cur)
		{
			if (key < cur->_key)
			{
				cur = cur->_left;
			}
			else if (key > cur->_key)
			{
				cur = cur->_right;
			}
			//相等就找到
			else
				return true;
		}
		return false;
	}
	bool Erase(const K& key)
	{
		if (_root == nullptr)
			return false;

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (key < cur->_key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (key > cur->_key)
			{
				parent = cur;
				cur = cur->_right;
			}
			//相等就找到
			else
			{
				//删除
				//左边空，即存在右子树，父亲指向右
				if (cur->_left == nullptr)
				{
					//单分支
					if (cur == _root)
					{
						_root = cur->_right;
						
					}
					else
					{
						//待删除结点在左
						if (cur == parent->_left)
						{
							parent->_left = cur->_right;
						}
						else
							parent->_right = cur->_right;
					}
					delete cur;
				}
				//右为空，即存在左子树,父亲指向左子树
				else if (cur->_right == nullptr)
				{
					//单分支
					if (cur == _root)
					{
						_root = cur->_left;

					}
					else
					{
						//待删除结点在左
						if (cur == parent->_left)
						{
							parent->_left = cur->_left;
						}
						else
							parent->_right = cur->_left;
					}
					delete cur;
				}
				//两边都不为空，即存在左右子树
				//以右边最小值替换
				else
				{
					Node* RightMinp = cur;
					Node* RightMin = cur->_right;
					//找右子树的最左边
					while (RightMin->_left)
					{
						RightMinp = RightMin;
						RightMin = RightMin->_left;
					}
					swap(RightMin->_key, cur->_key);//交换

					//左为空，存在右子树，父亲指向右
					if (RightMin == RightMinp->_left)
					{
						RightMinp->_left = RightMin->_right;
					}
					else
					{
						RightMinp->_right = RightMin->_right;
					}
					delete RightMin;
				}
				return true;
			}
		}
		return false;
	}
	void Inoder()
	{
		_Inoder(_root);
		cout << endl;
	}
private:
	Node* _root;
	void _Inoder(Node* root)
	{
		if (root == nullptr)
			return;
		_Inoder(root->_left);
		cout << root->_key << " ";
		_Inoder(root->_right);
	}
	Node* Copy(Node* root)
	{
		if (root == nullptr)
			return nullptr;
		Node* newroot = new Node(root->_key);//拷贝根
		newroot->_left = Copy(root->_left);//拷贝左
		newroot->_right = Copy(root->_right);//拷贝右
		return newroot;
	}

	void Destoy(Node* root)
	{
		if (root == nullptr)
			return;
		Destoy(root->_left);
		Destoy(root->_right);
		delete root;
	}
};

三、应用

两种模型

1.K模型

K模型：只有Key作为关键码，结构只需要存储Key即可，关键码即为需要搜索到的值。

如：检查单词是否拼写正确，具体实现方式

  • 将所有单词插入一棵二叉搜索树中，单词作为Key
  • 检查二叉搜索树中是否有这个单词存在，存在则正确，不在则错误！

上述实现的代码即为K模型！

2.KV 模型

KV：每一个关键码Key，都有与之对应的值Value，即<Key,Value>键值对。平时最常见的模型

比如：英汉词典，每个英文单词都有对应的中文意思，即<word,Chinese>键值对

还有统计单词出现的次数,即<Key,count>键值对。

3.K简单改造KV模型

实际上没有太大的改动

cpp 复制代码 
//节点类
template<class K,class V>
class BSTreeNode
{
public:
	BSTreeNode<K>* _left;
	BSTreeNode<K>* _right;
	K _key;
	V _value;
	BSTreeNode(const K& key,V& value)
		:_left(nullptr)
		, _right(nullptr)
		, _key(key)
		,_value(value)
	{}
};

插入和查找功能的改变
template<class K,class V>
class BSTree
{
	typedef BSTreeNode<K,V> Node;
public:
	bool Insert(const K& key, const V& value)
	{
		if (_root == nullptr)
		{
			_root = new Node(key, value);
			return true;
		}

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			//小于找左边
			if (key < cur->_key)
			{
				parent = cur;
				cur = cur->_left;
			}
			//大于找右边
			else if (key > cur->_key)
			{
				parent = cur;
				cur = cur->_right;
			}
			//不允许数据冗余,相等不插入
			else
			{
				return false;
			}
		}
		cur = new Node(key,value);
		if (key < parent->_key)
		{
			//放左边
			parent->_left = cur;
		}
		else
		{
			//放右边
			parent->_right = cur;
		}
		return true;
	}
	Node* Find(const K& key)
	{
		if (_root == nullptr)
			return nullptr;

		Node* cur = _root;
		while (cur)
		{
			if (key < cur->_key)
			{
				cur = cur->_left;
			}
			else if (key > cur->_key)
			{
				cur = cur->_right;
			}
			//相等就找到
			else
				return cur;
		}
		return nullptr;
	}
    ....................................
}
int main()
{
    BSTree<string, string> dict;
	dict.Insert("insert", "插入");
	dict.Insert("erase", "删除");
	dict.Insert("left", "左边");
	dict.Insert("string", "字符串");
    return 0;
}

注意：比较只是和Key有关，和Value没有任何的关系！Key不能修改，Value可以，因为Key修改，二叉树就乱了！

四、性能分析

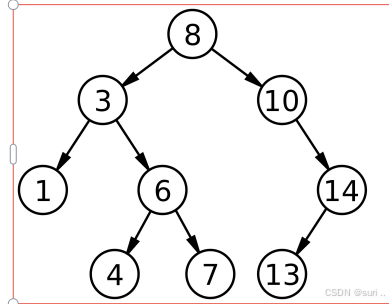
最优情况：二叉搜索树为完全二叉树(或者接近完全二叉树)，平均比较次数为高度次，即log_2N

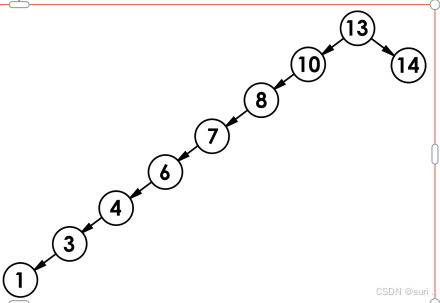
最坏情况：接近有序插入可能会退化成单支树，性能就大大的降低了

上述问题能否解决？肯定能，ALV树和红黑树就可以解决，可以看作是二叉搜索树的优化。敬请关注！

好了，铁子们，今天的内容就分享到这里，如果对你有所帮助，欢迎三连！你的支持永远是我的动力！！

相关推荐
泉崎1 小时前
11.7比赛总结
数据结构·算法
你好helloworld1 小时前
滑动窗口最大值
数据结构·算法·leetcode
JSU_曾是此间年少2 小时前
数据结构——线性表与链表
数据结构·c++·算法
sjsjs112 小时前
【数据结构-合法括号字符串】【hard】【拼多多面试题】力扣32. 最长有效括号
数据结构·leetcode
blammmp3 小时前
Java：数据结构-枚举
java·开发语言·数据结构
昂子的博客4 小时前
基础数据结构——队列（链表实现）
数据结构
lulu_gh_yu4 小时前
数据结构之排序补充
c语言·开发语言·数据结构·c++·学习·算法·排序算法
～yY…s<#>6 小时前
【刷题17】最小栈、栈的压入弹出、逆波兰表达式
c语言·数据结构·c++·算法·leetcode
XuanRanDev7 小时前
【每日一题】LeetCode - 三数之和
数据结构·算法·leetcode·1024程序员节
代码猪猪傻瓜coding7 小时前
力扣1 两数之和
数据结构·算法·leetcode
热门推荐
01【HarmonyOS】HUAWEI DevEco Studio 下载地址汇总02(欧拉)openEuler系统添加网卡文件配置流程、(欧拉)openEuler系统手动配置ipv6地址流程、(欧拉)openEuler系统网络管理说明03组基轨迹建模 GBTM的介绍与实现（Stata 或 R）04【AIGC】重塑未来的科技巨轮05全面解析：构建基于深度学习的安全帽检测系统（UI界面+YOLO代码+数据集）06【经验分享】Ubuntu22.04安装微信(linux官方版)07基于YOLOv10深度学习的CT扫描图像肾结石智能检测系统【python源码+Pyqt5界面+数据集+训练代码】深度学习实战、目标检测08Ubuntu 20.04使用Livox mid 360 测试 FAST_LIO09RAG 实践- Ollama+RagFlow 部署本地知识库10【TC3xx芯片】TC3xx芯片电源管理系统PMS详解