Python酷库之旅-第三方库Pandas(091)

目录

一、用法精讲

386、pandas.Series.plot.density方法

386-1、语法

386-2、参数

386-3、功能

386-4、返回值

386-5、说明

386-6、用法

386-6-1、数据准备

386-6-2、代码示例

386-6-3、结果输出

387、pandas.Series.plot.hist方法

387-1、语法

387-2、参数

387-3、功能

387-4、返回值

387-5、说明

387-6、用法

387-6-1、数据准备

387-6-2、代码示例

387-6-3、结果输出

388、pandas.Series.plot.kde方法

388-1、语法

388-2、参数

388-3、功能

388-4、返回值

388-5、说明

388-6、用法

388-6-1、数据准备

388-6-2、代码示例

388-6-3、结果输出

389、pandas.Series.plot.line方法

389-1、语法

389-2、参数

389-3、功能

389-4、返回值

389-5、说明

389-6、用法

389-6-1、数据准备

389-6-2、代码示例

389-6-3、结果输出

390、pandas.Series.plot.pie方法

390-1、语法

390-2、参数

390-3、功能

390-4、返回值

390-5、说明

390-6、用法

390-6-1、数据准备

390-6-2、代码示例

390-6-3、结果输出

二、推荐阅读

1、Python筑基之旅

2、Python函数之旅

3、Python算法之旅

4、Python魔法之旅

5、博客个人主页

一、用法精讲

386、pandas.Series.plot.density方法

386-1、语法

# 386、pandas.Series.plot.density方法
pandas.Series.plot.density(bw_method=None, ind=None, **kwargs)
Generate Kernel Density Estimate plot using Gaussian kernels.

In statistics, kernel density estimation (KDE) is a non-parametric way to estimate the probability density function (PDF) of a random variable. This function uses Gaussian kernels and includes automatic bandwidth determination.

Parameters:
bw_method
str, scalar or callable, optional
The method used to calculate the estimator bandwidth. This can be 'scott', 'silverman', a scalar constant or a callable. If None (default), 'scott' is used. See scipy.stats.gaussian_kde for more information.

ind
NumPy array or int, optional
Evaluation points for the estimated PDF. If None (default), 1000 equally spaced points are used. If ind is a NumPy array, the KDE is evaluated at the points passed. If ind is an integer, ind number of equally spaced points are used.

**kwargs
Additional keyword arguments are documented in DataFrame.plot().

Returns:
matplotlib.axes.Axes or numpy.ndarray of them.

386-2、参数

386-2-1、bw_method**(可选，默认值为None)****：**str,float或callable,指定用于估计密度的带宽(bandwidth)选择方法。

• 如果是str，可以使用'scott'或'silverman'，这是两种常用的带宽选择规则：
  • 'scott'：带宽= n\^{-1/(d+4)}，其中n是样本数量，d是数据维度。
  • 'silverman'：带宽= \\left(\\frac{n(d+2)}{4}\\right)\^{-1/(d+4)}。
• 如果是float，直接指定带宽的值。
• 如果是callable，可以传递自定义的带宽选择函数。
• 如果None，则使用默认的带宽选择方法(即scott)。

386-2-2、ind**(可选，默认值为None)****：**numpy.array或int,定义在绘制密度图时，密度估计的横坐标点(即用于评估密度估计的点)。

• 如果是int，则代表将横坐标划分为ind个等间隔的点。
• 如果是numpy.array，则指定评估密度估计的具体点。
• 如果None，则会在数据范围内自动生成一个等间隔的点集。

386-2-3、**kwargs**(可选)****：**用于传递给matplotlib的其他关键词参数，这些参数可以自定义图形的各种属性，比如颜色、线型、标签等。

386-3、功能

基于数据生成核密度估计图，它将数据的分布以平滑曲线的形式展示出来，便于观察数据的整体分布趋势以及其集中程度。

386-4、返回值

返回一个matplotlib.Axes对象，通过它可以进一步定制和显示图形，如果在交互式环境中使用(如Jupyter Notebook)，图形会自动显示，通过这些参数的调节，你可以控制核密度估计图的平滑程度、评估点的数量以及图形的外观。

386-5、说明

使用场景：

386-5-1、数据分布的可视化： KDE图可以用来直观地显示数据的概率密度分布，与直方图类似，但相比之下更加平滑和连续，这在需要理解数据的分布特征时非常有用

386-5-2、与正态分布的比较： 在分析数据时，KDE图可以用来与标准正态分布进行比较，以判断数据是否符合正态分布，或识别出数据的偏态、峰度等特征。

386-5-3、多组数据的比较： 通过绘制多个系列的KDE图，可以比较不同数据集的分布差异。例如，比较不同组别的特征分布情况，识别组间差异。

386-5-4、异常值检测： KDE图可以帮助识别数据中的异常值或极端值，这些点通常位于密度非常低的区域。

386-5-5、替代直方图： 在数据量较小时，直方图可能不够平滑且受区间划分影响较大，KDE图可以作为直方图的替代品，提供更平滑的分布曲线。

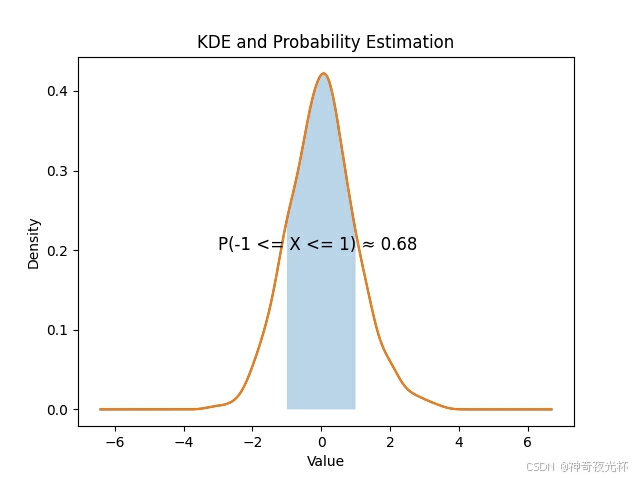
**386-5-6、概率估计：**在某些场景下，可以利用KDE图进行概率密度的估计，从而进一步计算数据点落在某个区间内的概率。

386-6、用法

386-6-1、数据准备

无

386-6-2、代码示例

# 386、pandas.Series.plot.density方法
# 386-1、数据分布的可视化
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 生成服从正态分布的随机数据
data = np.random.normal(loc=0, scale=1, size=1000)
series = pd.Series(data)
# 绘制核密度估计图
series.plot.density()
plt.title('Kernel Density Estimation of Normally Distributed Data')
plt.xlabel('Value')
plt.ylabel('Density')
plt.show()

# 386-2、与正态分布的比较
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 生成服从正态分布的随机数据
data = np.random.normal(loc=0, scale=1, size=1000)
series = pd.Series(data)
# 绘制核密度估计图
series.plot.density(label='KDE')
# 绘制标准正态分布的概率密度函数
x = np.linspace(-4, 4, 1000)
plt.plot(x, norm.pdf(x), label='Normal Distribution', linestyle='--')
plt.title('KDE vs Normal Distribution')
plt.xlabel('Value')
plt.ylabel('Density')
plt.legend()
plt.show()

# 386-3、多组数据的比较
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 生成两组不同分布的随机数据
data1 = np.random.normal(loc=0, scale=1, size=1000)
data2 = np.random.normal(loc=2, scale=1.5, size=1000)
series1 = pd.Series(data1)
series2 = pd.Series(data2)
# 绘制两组数据的核密度估计图
series1.plot.density(label='Group 1')
series2.plot.density(label='Group 2')
plt.title('Comparison of KDE for Two Groups')
plt.xlabel('Value')
plt.ylabel('Density')
plt.legend()
plt.show()

# 386-4、异常值检测
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 生成服从正态分布的随机数据，并添加异常值
data = np.random.normal(loc=0, scale=1, size=1000)
outliers = np.random.uniform(low=-8, high=8, size=10)
data_with_outliers = np.concatenate([data, outliers])
series = pd.Series(data_with_outliers)
# 绘制核密度估计图
series.plot.density()
plt.title('KDE with Outliers')
plt.xlabel('Value')
plt.ylabel('Density')
plt.show()

# 386-5、替代直方图
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 生成较少的数据点
data = np.random.normal(loc=0, scale=1, size=50)
series = pd.Series(data)
# 绘制直方图和核密度估计图
series.plot.hist(density=True, alpha=0.5, bins=10, label='Histogram')
series.plot.density(label='KDE')
plt.title('Histogram vs KDE')
plt.xlabel('Value')
plt.ylabel('Density')
plt.legend()
plt.show()

# 386-6、概率估计
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import simps
# 生成服从正态分布的随机数据
data = np.random.normal(loc=0, scale=1, size=1000)
series = pd.Series(data)
# 绘制核密度估计图
ax = series.plot.density()
plt.title('KDE and Probability Estimation')
plt.xlabel('Value')
plt.ylabel('Density')
# 计算在区间[-1, 1]内的概率
kde = series.plot.density().get_lines()[0].get_data()
x_values = kde[0]
y_values = kde[1]
# 找到x在[-1, 1]之间的索引
mask = (x_values >= -1) & (x_values <= 1)
probability = simps(y_values[mask], x_values[mask])
plt.fill_between(x_values, y_values, where=mask, alpha=0.3)
plt.text(-3, 0.2, f'P(-1 <= X <= 1) ≈ {probability:.2f}', fontsize=12)
plt.show()

386-6-3、结果输出

# 386、pandas.Series.plot.density方法
# 386-1、数据分布的可视化
# 见图1

# 386-2、与正态分布的比较
# 见图2

# 386-3、多组数据的比较
# 见图3

# 386-4、异常值检测
# 见图4

# 386-5、替代直方图
# 见图5

# 386-6、概率估计
# 见图6

图1：

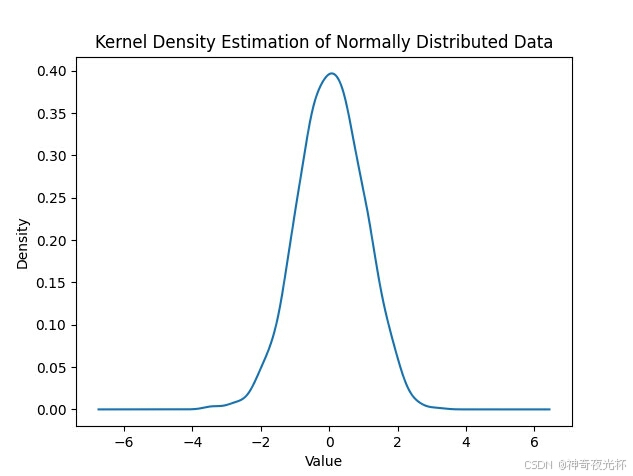
图2：

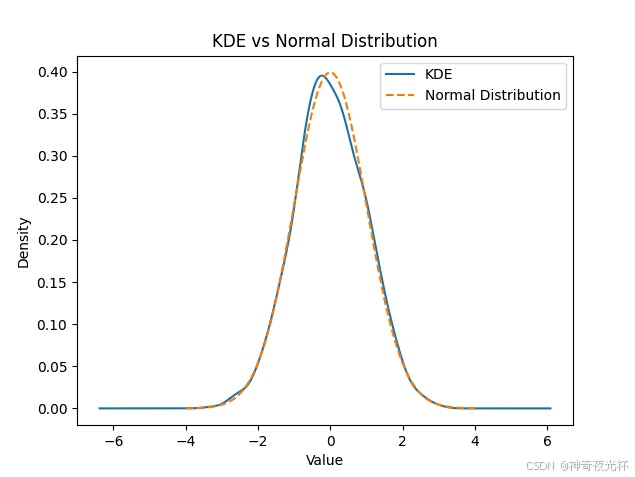
图3：

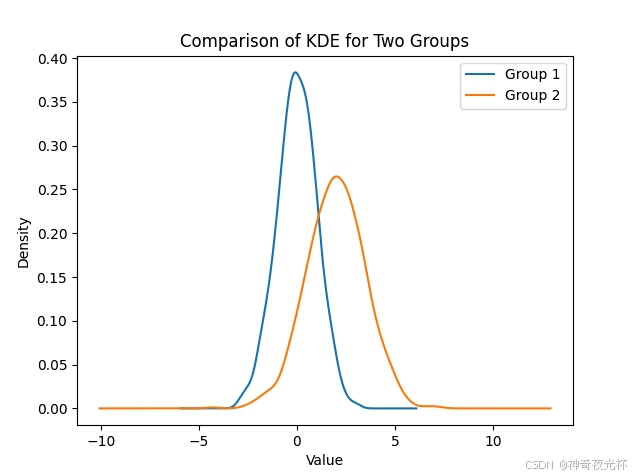
图4：

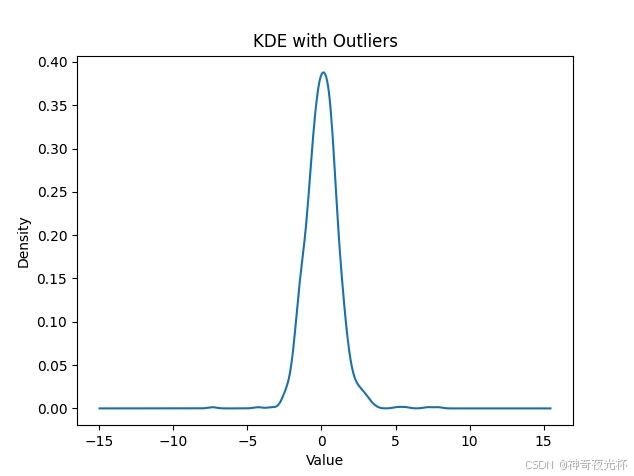
图5：

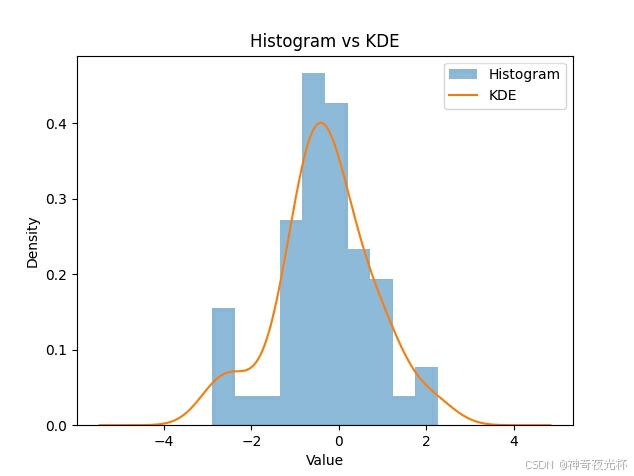
图6：

387、pandas.Series.plot.hist方法

387-1、语法

# 387、pandas.Series.plot.hist方法
pandas.Series.plot.hist(by=None, bins=10, **kwargs)
Draw one histogram of the DataFrame's columns.

A histogram is a representation of the distribution of data. This function groups the values of all given Series in the DataFrame into bins and draws all bins in one matplotlib.axes.Axes. This is useful when the DataFrame's Series are in a similar scale.

Parameters:
bystr or sequence, optional
Column in the DataFrame to group by.

Changed in version 1.4.0: Previously, by is silently ignore and makes no groupings

binsint, default 10
Number of histogram bins to be used.

**kwargs
Additional keyword arguments are documented in DataFrame.plot().

Returns:
class:
matplotlib.AxesSubplot
Return a histogram plot.

387-2、参数

387-2-1、by**(可选，默认值为None)****：**一般用于DataFrame，用于指定根据哪个列对数据进行分组，对于Series对象来说，这个参数没有作用，因此可以忽略。

387-2-2、bins**(可选，默认值为10)****：**用于指定直方图的柱子(区间)数量，可以是一个整数，表示将数据分为多少个区间；也可以是一个序列，直接指定每个区间的边界；如果你设置为整数n，那么数据会被自动分为n个区间；如果给出的是一组值，表示你希望这些值作为区间边界。

387-2-3、**kwargs**(可选)****：**允许你传递更多的关键字参数来定制直方图的外观和行为，常见的参数包括：

• **color：**指定直方图的颜色。
• **alpha：**透明度，取值范围为0到1。
• **grid：**是否显示网格线，布尔值。

387-3、功能

生成并显示一个直方图，帮助用户直观地观察数据的分布情况，通过设置不同的参数，用户可以调整直方图的区间数量、颜色、透明度等，生成更符合需求的图表。

387-4、返回值

调用这个方法后，会返回一个matplotlib.axes.Axes对象，这是一个Matplotlib库中的对象，表示生成的图表，可以进一步通过这个对象对图表进行操作，比如调整坐标轴、标题、标签等。

387-5、说明

使用场景：

**387-5-1、数据分布分析：**当你有一组连续的数据时，直方图是最常用的工具之一，用于了解数据的分布。例如，你有一组实验数据，想要了解这些数据是否服从正态分布，这时可以使用直方图来初步判断。

**387-5-2、异常值检测：**通过直方图可以快速发现数据中的异常值。例如，在数据中某些区间的值出现频率非常低，甚至有异常高或低的数据点，直方图可以帮助你识别这些异常。

**387-5-3、数据预处理：**在对数据进行预处理时，尤其是需要进行特征工程时，了解数据的分布是非常关键的，通过直方图，你可以确定是否需要对数据进行变换，例如对数变换、标准化或归一化。

**387-5-4、比较不同子集的数据分布：**在有多个子集的数据时，使用直方图可以比较不同子集之间的分布差异。例如，比较不同性别、不同年龄段的人群的某项指标分布。

**387-5-5、模型评估：**在机器学习中，直方图也被用来评估模型的输出分布，特别是在回归任务中，通过直方图来分析预测值的分布与实际值的分布是否接近。

387-6、用法

387-6-1、数据准备

无

387-6-2、代码示例

# 387、pandas.Series.plot.hist方法
# 387-1、数据分布分析
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 生成一组服从正态分布的学生成绩数据
scores = pd.Series(np.random.normal(loc=70, scale=10, size=1000))
# 绘制成绩分布的直方图
plt.figure(figsize=(10, 6))
scores.plot.hist(bins=20, color='skyblue', edgecolor='black')
plt.title('Distribution of Student Scores')
plt.xlabel('Scores')
plt.ylabel('Frequency')
plt.grid(True)
plt.show()

# 387-2、异常值检测
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 生成一组标准正态分布的传感器数据
sensor_data = pd.Series(np.random.randn(1000))
# 绘制传感器数据的直方图
plt.figure(figsize=(10, 6))
sensor_data.plot.hist(bins=50, color='red', edgecolor='black')
plt.title('Distribution of Sensor Data')
plt.xlabel('Sensor Values')
plt.ylabel('Frequency')
plt.grid(True)
plt.show()

# 387-3、数据预处理
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 生成一组带有偏态的销售数据
sales_data = pd.Series(np.random.exponential(scale=2, size=1000))
# 绘制原始销售数据的直方图
plt.figure(figsize=(10, 6))
sales_data.plot.hist(bins=30, color='green', edgecolor='black')
plt.title('Distribution of Sales Data')
plt.xlabel('Sales')
plt.ylabel('Frequency')
plt.grid(True)
plt.show()

# 387-4、比较不同子集的数据分布
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 生成男性和女性的收入数据
income_male = pd.Series(np.random.normal(loc=50000, scale=8000, size=1000))
income_female = pd.Series(np.random.normal(loc=48000, scale=7000, size=1000))
# 绘制男性和女性收入分布的直方图
plt.figure(figsize=(10, 6))
income_male.plot.hist(bins=20, alpha=0.5, color='blue', edgecolor='black', label='Male')
income_female.plot.hist(bins=20, alpha=0.5, color='pink', edgecolor='black', label='Female')
plt.title('Income Distribution by Gender')
plt.xlabel('Income')
plt.ylabel('Frequency')
plt.legend()
plt.grid(True)
plt.show()

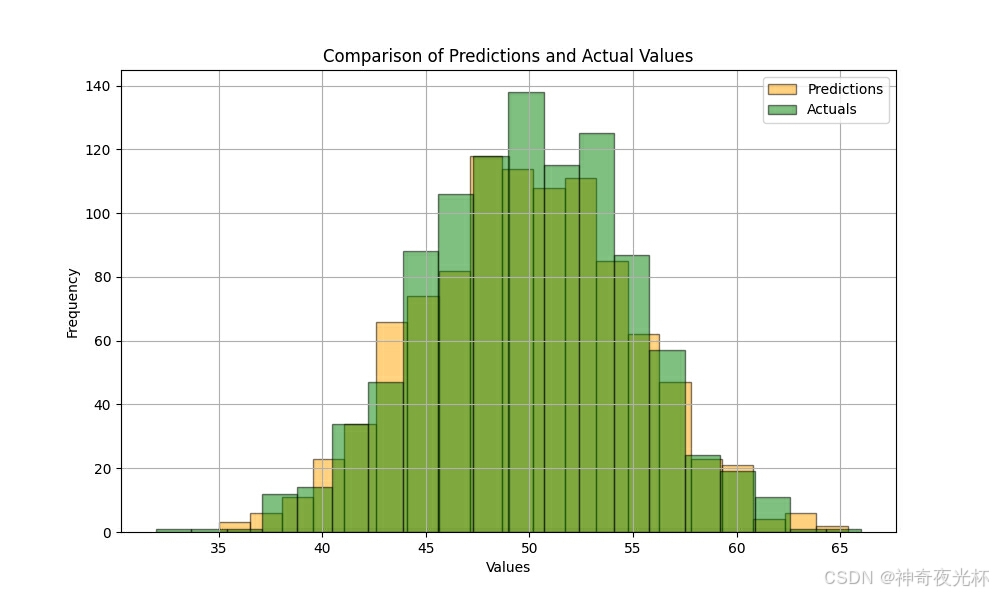
# 387-5、模型评估
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 生成模型的预测值和实际值
predictions = pd.Series(np.random.normal(loc=50, scale=5, size=1000))
actuals = pd.Series(np.random.normal(loc=50, scale=5, size=1000))
# 绘制预测值和实际值分布的直方图
plt.figure(figsize=(10, 6))
predictions.plot.hist(bins=20, alpha=0.5, color='orange', edgecolor='black', label='Predictions')
actuals.plot.hist(bins=20, alpha=0.5, color='green', edgecolor='black', label='Actuals')
plt.title('Comparison of Predictions and Actual Values')
plt.xlabel('Values')
plt.ylabel('Frequency')
plt.legend()
plt.grid(True)
plt.show()

387-6-3、结果输出

# 387、pandas.Series.plot.hist方法
# 387-1、数据分布分析
# 见图7

# 387-2、异常值检测
# 见图8

# 387-3、数据预处理
# 见图9

# 387-4、比较不同子集的数据分布
# 见图10

# 387-5、模型评估
# 见图11

图7：

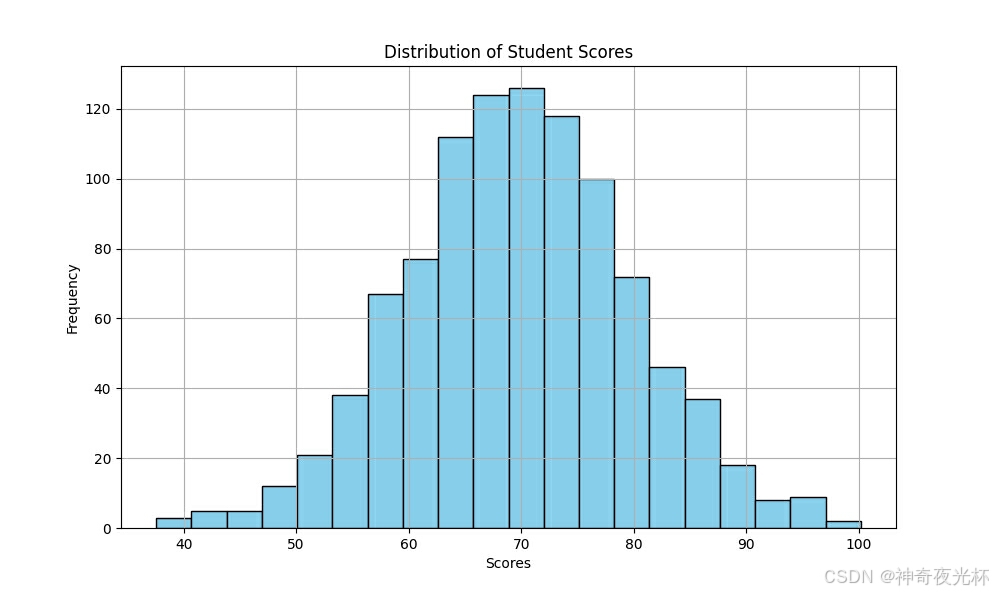
图8：

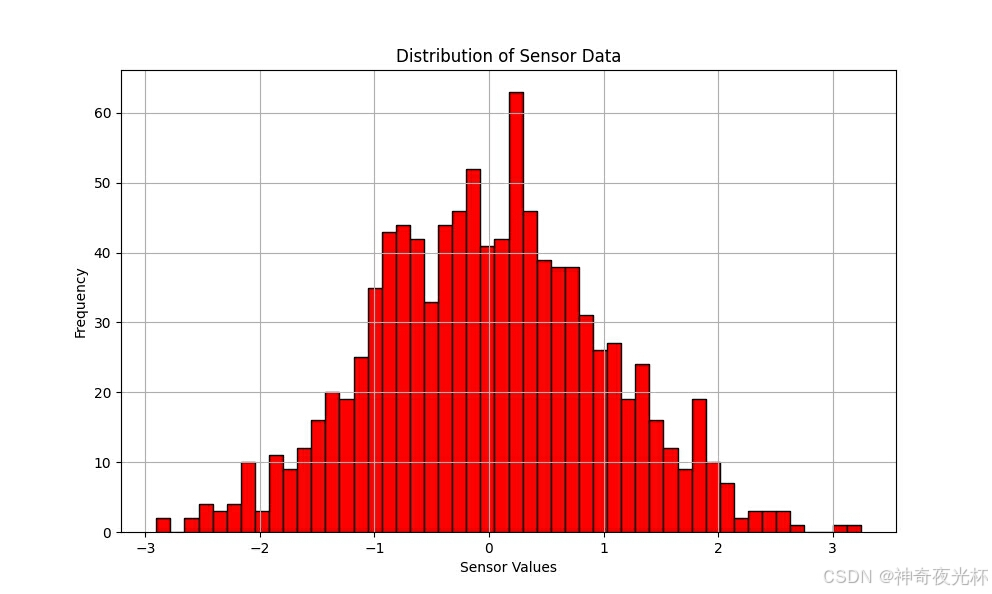
图9：

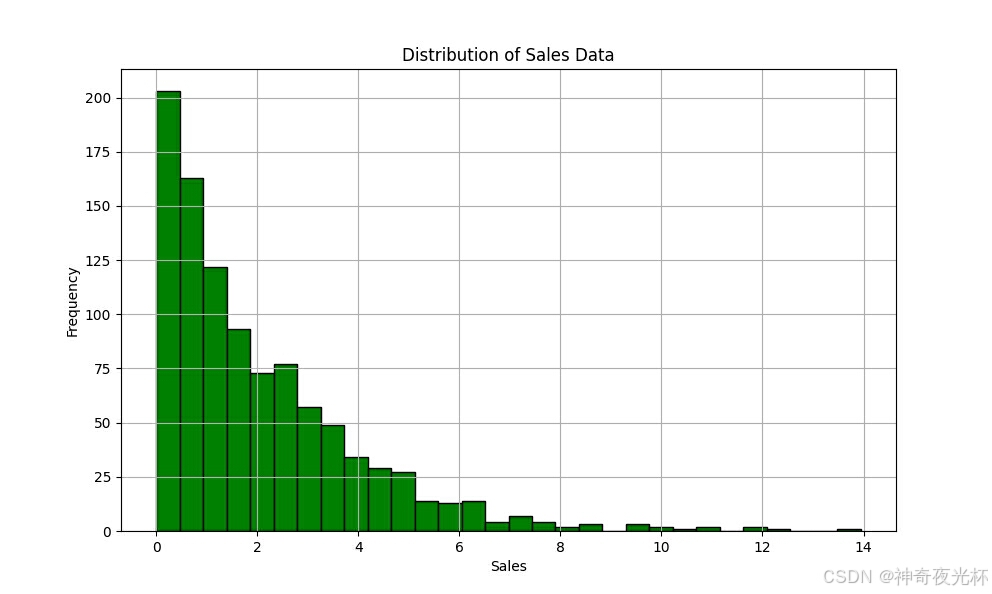
图10：

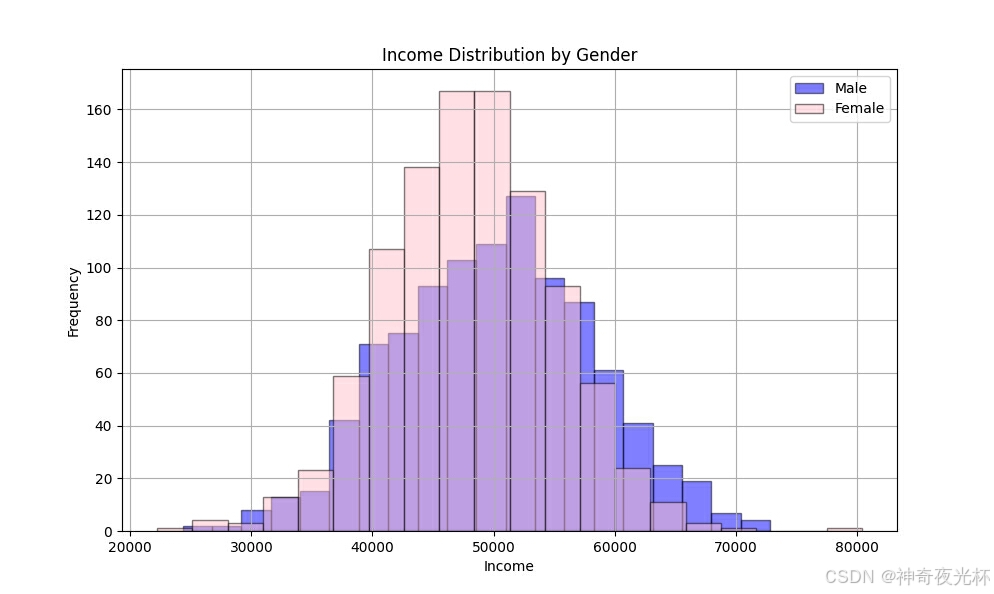
图11：

388、pandas.Series.plot.kde方法

388-1、语法

# 388、pandas.Series.plot.kde方法
pandas.Series.plot.kde(bw_method=None, ind=None, **kwargs)
Generate Kernel Density Estimate plot using Gaussian kernels.

In statistics, kernel density estimation (KDE) is a non-parametric way to estimate the probability density function (PDF) of a random variable. This function uses Gaussian kernels and includes automatic bandwidth determination.

Parameters:
bw_method
str, scalar or callable, optional
The method used to calculate the estimator bandwidth. This can be 'scott', 'silverman', a scalar constant or a callable. If None (default), 'scott' is used. See scipy.stats.gaussian_kde for more information.

ind
NumPy array or int, optional
Evaluation points for the estimated PDF. If None (default), 1000 equally spaced points are used. If ind is a NumPy array, the KDE is evaluated at the points passed. If ind is an integer, ind number of equally spaced points are used.

**kwargs
Additional keyword arguments are documented in DataFrame.plot().

Returns:
matplotlib.axes.Axes or numpy.ndarray of them.

388-2、参数

388-2-1、bw_method**(可选，默认值为None)****：**str,float或callable,指定用于估计密度的带宽(bandwidth)选择方法。

• 如果是str，可以使用'scott'或'silverman'，这是两种常用的带宽选择规则：
  • 'scott'：带宽= n\^{-1/(d+4)}，其中n是样本数量，d是数据维度。
  • 'silverman'：带宽= \\left(\\frac{n(d+2)}{4}\\right)\^{-1/(d+4)}。
• 如果是float，直接指定带宽的值。
• 如果是callable，可以传递自定义的带宽选择函数。
• 如果None，则使用默认的带宽选择方法(即scott)。

388-2-2、ind**(可选，默认值为None)****：**numpy.array或int,定义在绘制密度图时，密度估计的横坐标点(即用于评估密度估计的点)。

• 如果是int，则代表将横坐标划分为ind个等间隔的点。
• 如果是numpy.array，则指定评估密度估计的具体点。
• 如果None，则会在数据范围内自动生成一个等间隔的点集。

388-2-3、**kwargs**(可选)****：**用于传递给matplotlib的其他关键词参数，这些参数可以自定义图形的各种属性，比如颜色、线型、标签等。

388-3、功能

用于绘制核密度估计图，这是一种平滑的直方图，它通过使用核函数估计数据的概率密度，相比于直方图，KDE提供了一种更平滑的方式来观察数据的分布特征。

388-4、返回值

返回一个matplotlib的Axes对象，该对象表示绘制的图形，你可以进一步修改它(例如添加标题、标签等)，或者直接显示它。

388-5、说明

使用场景：

388-5-1、数据分布的平滑估计：当你希望观察数据的概率密度分布时，KDE提供了比直方图更平滑的视觉效果，它能够帮助你识别数据的集中区域、离群值以及分布的整体形态。

388-5-2、多模态分布的识别：与直方图不同，KDE更容易展示出多模态(多个峰值)的分布特征，适用于识别数据中是否存在多个不同的子群体。

388-5-3、对比不同数据集的分布：在比较多个数据集的分布时，可以使用KDE绘制每个数据集的密度曲线，从而方便地进行对比分析，例如判断两个数据集的中心趋势、分布宽度是否相似。

388-5-4、非参数估计：KDE是一种非参数方法，无需假设数据遵循某种特定分布(如正态分布)，非常适合在没有明确分布假设的情况下进行分析。

388-5-5、高维数据的边缘分布分析：对于高维数据集，可以通过对各维度分别使用KDE，来分析各个维度的边缘分布，从而理解数据的结构和特征。

388-6、用法

388-6-1、数据准备

无

388-6-2、代码示例

# 388、pandas.Series.plot.kde方法
# 388-1、数据分布的平滑估计
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 生成随机数据
data = np.random.normal(loc=0, scale=1, size=1000)
series = pd.Series(data)
# 使用KDE估计数据分布
series.plot.kde()
# 添加标题和标签
plt.title('KDE of Normally Distributed Data')
plt.xlabel('Value')
plt.ylabel('Density')
plt.show()

# 388-2、多模态分布的识别
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 生成双峰数据
data = np.concatenate([np.random.normal(loc=-2, scale=1, size=500),
                       np.random.normal(loc=3, scale=0.5, size=500)])
series = pd.Series(data)
# 使用KDE估计多模态分布
series.plot.kde()
# 添加标题和标签
plt.title('KDE of Bimodal Distribution')
plt.xlabel('Value')
plt.ylabel('Density')
plt.show()

# 388-3、对比不同数据集的分布
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 生成两个不同的数据集
data1 = np.random.normal(loc=0, scale=1, size=1000)
data2 = np.random.normal(loc=2, scale=1.5, size=1000)
series1 = pd.Series(data1)
series2 = pd.Series(data2)
# 使用KDE对比两个数据集的分布
series1.plot.kde(label='Dataset 1', linestyle='--')
series2.plot.kde(label='Dataset 2', linestyle='-')
# 添加标题、标签和图例
plt.title('Comparison of Two Distributions Using KDE')
plt.xlabel('Value')
plt.ylabel('Density')
plt.legend()
plt.show()

# 388-4、非参数估计
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 生成非正态分布的数据
data = np.random.exponential(scale=1, size=1000)
series = pd.Series(data)
# 使用KDE进行非参数估计
series.plot.kde()
# 添加标题和标签
plt.title('KDE of Exponential Distribution')
plt.xlabel('Value')
plt.ylabel('Density')
plt.show()

# 388-5、高维数据的边缘分布分析
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 生成高维数据集（例如二维）
data = np.random.multivariate_normal(mean=[0, 0], cov=[[1, 0.5], [0.5, 1]], size=1000)
df = pd.DataFrame(data, columns=['X1', 'X2'])
# 分别绘制每个维度的边缘分布
df['X1'].plot.kde(label='X1')
df['X2'].plot.kde(label='X2')
# 添加标题、标签和图例
plt.title('KDE of Marginal Distributions for Two Dimensions')
plt.xlabel('Value')
plt.ylabel('Density')
plt.legend()
plt.show()

388-6-3、结果输出

# 388、pandas.Series.plot.kde方法
# 388-1、数据分布的平滑估计
# 见图12

# 388-2、多模态分布的识别
# 见图13

# 388-3、对比不同数据集的分布
# 见图14

# 388-4、非参数估计
# 见图15

# 388-5、高维数据的边缘分布分析
# 见图16

图12：

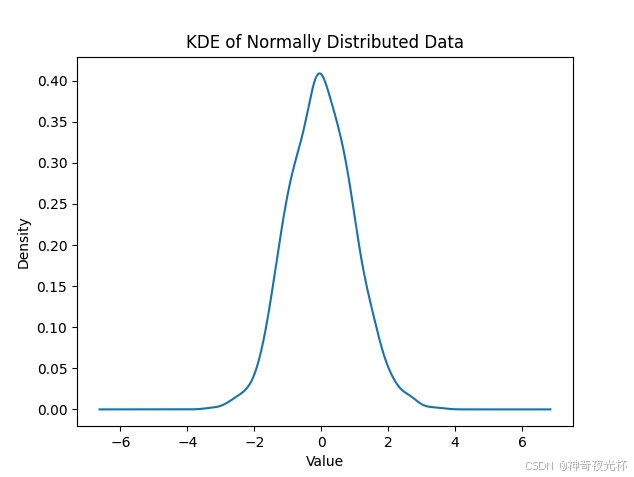
图13：

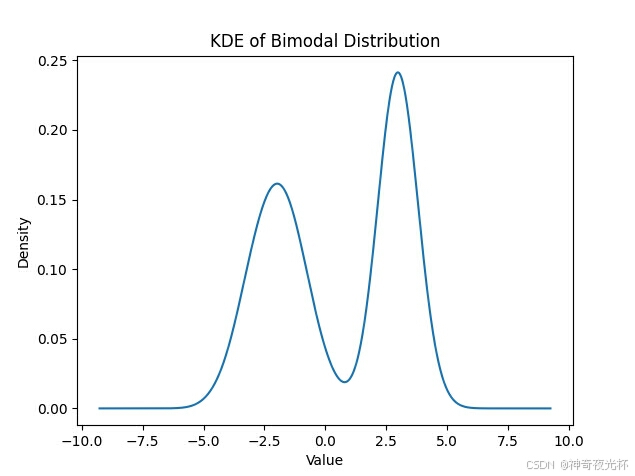
图14：

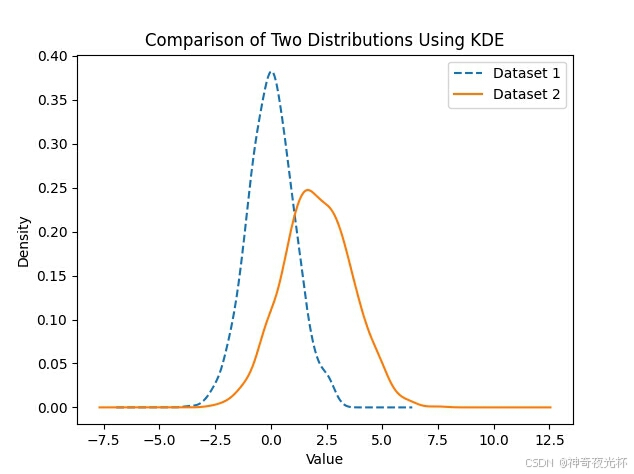
图15：

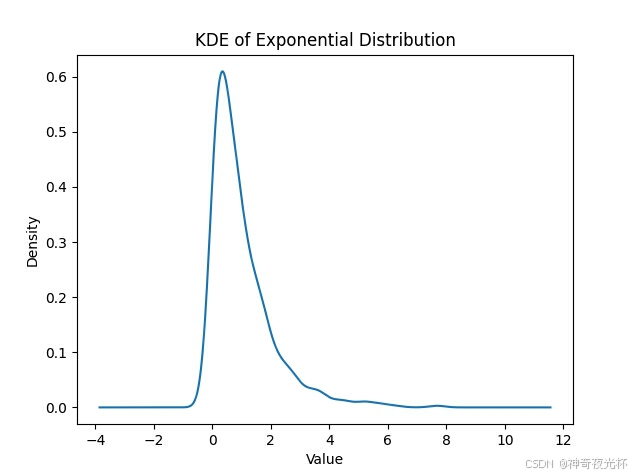
图16：

389、pandas.Series.plot.line方法

389-1、语法

# 389、pandas.Series.plot.line方法
pandas.Series.plot.line(x=None, y=None, **kwargs)
Plot Series or DataFrame as lines.

This function is useful to plot lines using DataFrame's values as coordinates.

Parameters:
x
label or position, optional
Allows plotting of one column versus another. If not specified, the index of the DataFrame is used.

y
label or position, optional
Allows plotting of one column versus another. If not specified, all numerical columns are used.

color
str, array-like, or dict, optional
The color for each of the DataFrame's columns. Possible values are:

A single color string referred to by name, RGB or RGBA code,
for instance 'red' or '#a98d19'.

A sequence of color strings referred to by name, RGB or RGBA
code, which will be used for each column recursively. For instance ['green','yellow'] each column's line will be filled in green or yellow, alternatively. If there is only a single column to be plotted, then only the first color from the color list will be used.

A dict of the form {column namecolor}, so that each column will be
colored accordingly. For example, if your columns are called a and b, then passing {'a': 'green', 'b': 'red'} will color lines for column a in green and lines for column b in red.

**kwargs
Additional keyword arguments are documented in DataFrame.plot().

Returns:
matplotlib.axes.Axes or np.ndarray of them
An ndarray is returned with one matplotlib.axes.Axes per column when subplots=True.

389-2、参数

389-2-1、x**(可选，默认值为None)****：**用于指定x轴的数据，如果未指定，默认情况下，使用Series的索引作为x轴数据。

389-2-2、y**(可选，默认值为None)****：**对于Series而言不是特别常用，因为Series是一维的，如果你希望显式指定y轴的数据，可以传递列名或其位置。

389-2-3、color**(可选，默认值为None)****：**用于指定线条颜色，可以使用颜色名(如'red')、十六进制颜色码(如'#FF5733')或RGB(A)值。

389-2-4、label**(可选，默认值为None)****：**指定图例的标签，如果不提供，将自动使用Series的名称。

389-2-5、style**(可选，默认值为None)****：**指定线条的样式，如'-'(实线)、'--'(虚线)等，可以结合颜色、标记、线条风格使用，如'ro--'表示红色虚线且带圆圈标记。

389-2-6、alpha**(可选，默认值为None)****：**用于设置线条的透明度，取值范围为[0, 1]，其中0表示完全透明，1表示完全不透明。

389-2-7、ax**(可选，默认值为None)****：**指定绘图使用的matplotlib轴对象，如果不提供，将在当前轴上进行绘图。

389-2-8、figsize**(可选，默认值为None)****：**指定图的尺寸，如(width,height)，尺寸单位为英寸。

389-2-9、grid**(可选，默认值为None)****：**指定是否在图中添加网格线，默认情况下，根据pandas配置确定。

389-2-10、legend**(可选，默认值为False)****：**指定是否显示图例，如果为True，则显示图例。

389-2-11、title**(可选，默认值为None)****：**指定图表的标题。

389-2-12、ylim**(可选，默认值为None)****：**指定y轴的范围，如(ymin,ymax)，这可以用来限制y轴的值范围。

389-2-13、rot**(可选，默认值为None)****：**指定x轴标签的旋转角度。

389-2-14、logy**(可选，默认值为False)****：**指定是否使用对数刻度显示y轴数据。

389-2-15、use_index**(可选，默认值为True)****：**指定是否使用Series的索引作为x轴标签，如果为False，则使用RangeIndex。

389-2-16、secondary_y**(可选，默认值为False)****：**指定是否在第二y轴上绘制。

389-2-17、**kwargs**(可选)****：**其他传递给matplotlib plot函数的参数，如linewidth、linestyle、marker等。

389-3、功能

用于绘制线图，通过将Series中的值作为y轴数据，索引作为x轴数据(或通过指定x数据)，可以帮助快速可视化数据的走势和变化，它是对Series数据进行可视化的简单方法，适用于展示时间序列、连续数值等。

389-4、返回值

返回一个matplotlib.axes.Axes对象，表示图形的坐标轴，可以通过该对象进一步定制图形，比如调整标签、修改标题等，如果直接调用该方法而不作其他处理，会在当前活动的图形窗口中显示所绘制的线图。

389-5、说明

使用场景：

**389-5-1、时间序列分析：**用于绘制时间序列数据，例如股票价格、气温变化、销售额等，帮助分析数据随时间的趋势和波动。

**389-5-2、数据探索：**在数据分析的早期阶段，通过绘制线图来识别数据中的模式、季节性和异常值，为后续的数据清洗和建模提供直观的信息。

389-5-3、对比分析： 如果有多个线性数据系列，可以在同一图表中绘制多条线，便于对不同系列进行比较(虽然主要是对DataFrame的plot方法更为常用)。

**389-5-4、结果展示：**研究报告或商业报告中，用于直观展示分析结果，帮助读者理解数据背后的含义。

**389-5-5、监控指标：**在实时数据监控场景中使用，及时观察某些关键指标的变化，例如监控服务器性能指标、销售业绩等。

**389-5-6、算法调优：**在机器学习模型的训练和验证阶段，通过绘制损失函数或准确率随训练轮次的变化曲线，帮助判断模型的训练和调优效果。

389-6、用法

389-6-1、数据准备

无

389-6-2、代码示例

# 389、pandas.Series.plot.line方法
# 389-1、时间序列分析
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib
# 配置字体，确保中文字符正常显示
matplotlib.rcParams['font.sans-serif'] = ['Microsoft YaHei']
matplotlib.rcParams['axes.unicode_minus'] = False  # 解决负号 '-' 显示问题
# 创建时间序列数据
date_range = pd.date_range(start='2024-01-01', periods=100)
data = pd.Series(range(100), index=date_range)
# 绘制时间序列线图
data.plot.line(title='时间序列分析', xlabel='日期', ylabel='值', grid=True)
plt.show()

# 389-2、数据探索
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
# 配置字体，确保中文字符正常显示
matplotlib.rcParams['font.sans-serif'] = ['Microsoft YaHei']
matplotlib.rcParams['axes.unicode_minus'] = False  # 解决负号 '-' 显示问题
# 生成模拟数据
np.random.seed(0)
data = pd.Series(np.random.randn(100).cumsum(), name='随机数据')
# 绘制线图以探索数据
data.plot.line(title='随机数据探索', xlabel='索引', ylabel='累积和', grid=True)
plt.show()

# 389-3、对比分析
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib
# 配置字体，确保中文字符正常显示
matplotlib.rcParams['font.sans-serif'] = ['Microsoft YaHei']
matplotlib.rcParams['axes.unicode_minus'] = False  # 解决负号 '-' 显示问题
# 创建两组数据
data1 = pd.Series([1, 3, 2, 5, 4], name='数据1')
data2 = pd.Series([2, 2, 4, 3, 5], name='数据2')
# 绘制多个线图进行对比
plt.figure()
data1.plot.line(label='数据1', marker='o')
data2.plot.line(label='数据2', marker='x')
plt.title('对比分析')
plt.xlabel('索引')
plt.ylabel('值')
plt.legend()
plt.grid()
plt.show()

# 389-4、结果展示
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib
# 配置字体，确保中文字符正常显示
matplotlib.rcParams['font.sans-serif'] = ['Microsoft YaHei']
matplotlib.rcParams['axes.unicode_minus'] = False  # 解决负号 '-' 显示问题
# 假设这些是产品销售额
sales_data = pd.Series([100, 150, 300, 250, 400], index=['Q1', 'Q2', 'Q3', 'Q4', 'Q5'], name='季度销售')
# 绘制结果展示图
sales_data.plot.line(title='季度销售额', xlabel='季度', ylabel='销售额', marker='o', grid=True)
plt.show()

# 389-5、监控指标
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib
# 配置字体，确保中文字符正常显示
matplotlib.rcParams['font.sans-serif'] = ['Microsoft YaHei']
matplotlib.rcParams['axes.unicode_minus'] = False  # 解决负号 '-' 显示问题
# 模拟服务器CPU使用率数据
cpu_usage = pd.Series([30, 45, 60, 40, 70, 80, 100, 90, 85, 75], name='CPU使用率')
# 绘制监控图
cpu_usage.plot.line(title='CPU使用率监控', xlabel='时间点', ylabel='使用率 (%)', marker='o', grid=True)
plt.show()

# 389-6、算法调优
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib
# 配置字体，确保中文字符正常显示
matplotlib.rcParams['font.sans-serif'] = ['Microsoft YaHei']
matplotlib.rcParams['axes.unicode_minus'] = False  # 解决负号 '-' 显示问题
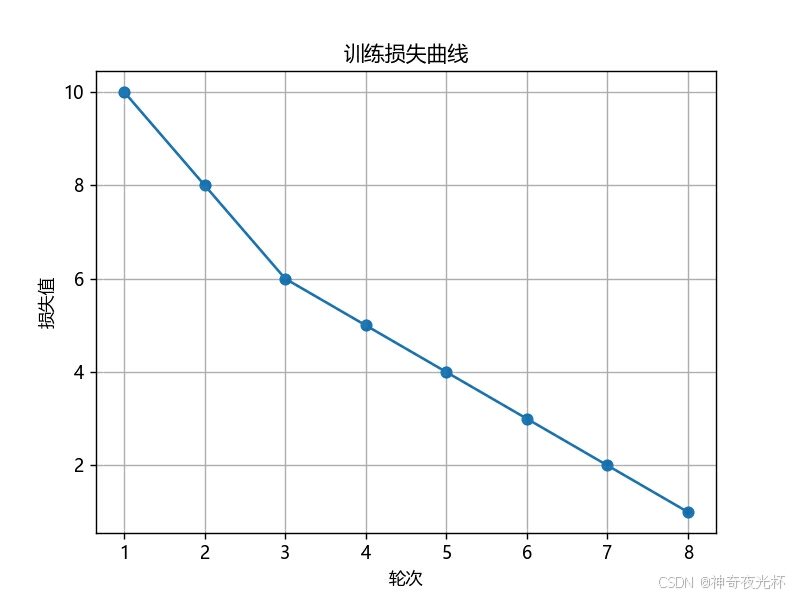
# 模拟训练过程中的损失值
epochs = pd.Series([10, 8, 6, 5, 4, 3, 2, 1], name='训练损失', index=range(1, 9))
# 绘制损失值图
epochs.plot.line(title='训练损失曲线', xlabel='轮次', ylabel='损失值', marker='o', grid=True)
plt.show()

389-6-3、结果输出

# 389、pandas.Series.plot.line方法
# 389-1、时间序列分析
# 见图17

# 389-2、数据探索
# 见图18

# 389-3、对比分析
# 见图19

# 389-4、结果展示
# 见图20

# 389-5、监控指标
# 见图21

# 389-6、算法调优
# 见图22

图17：

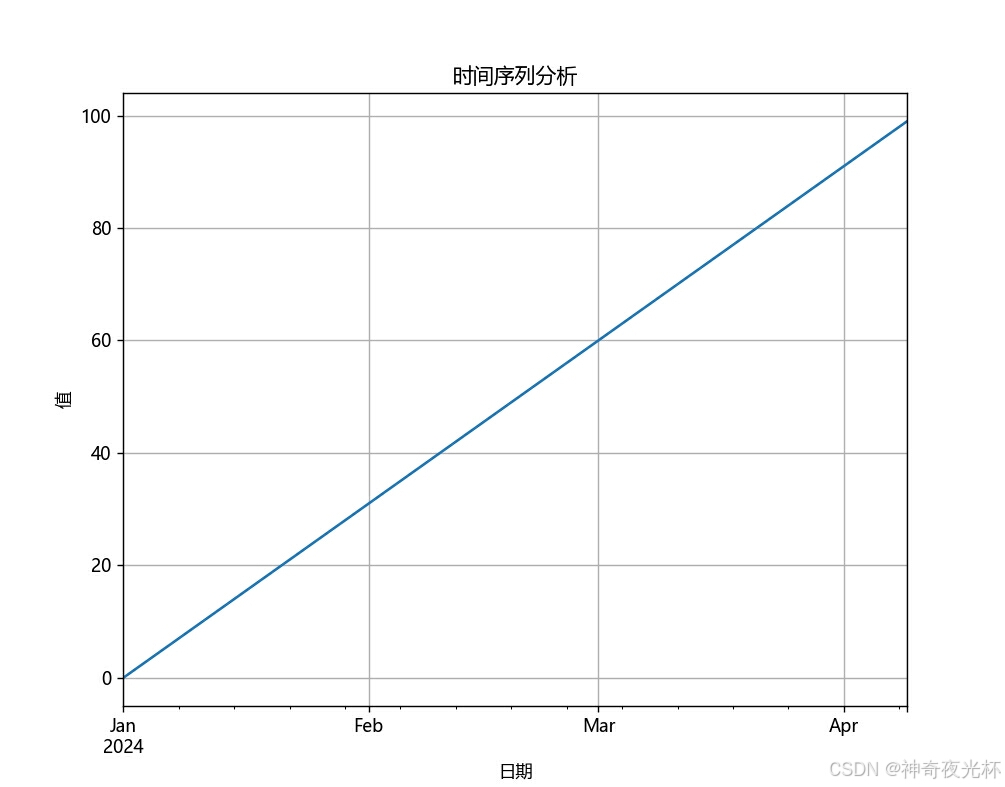
图18：

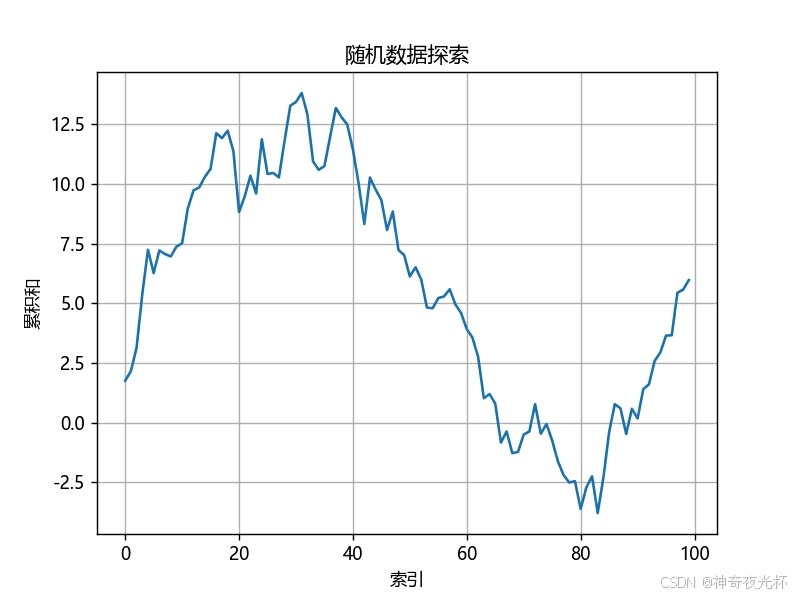
图19：

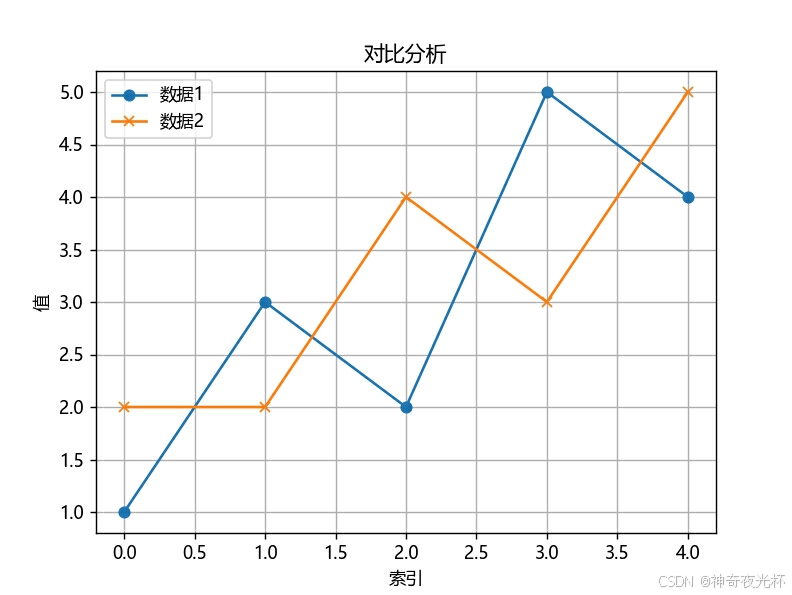
图20：

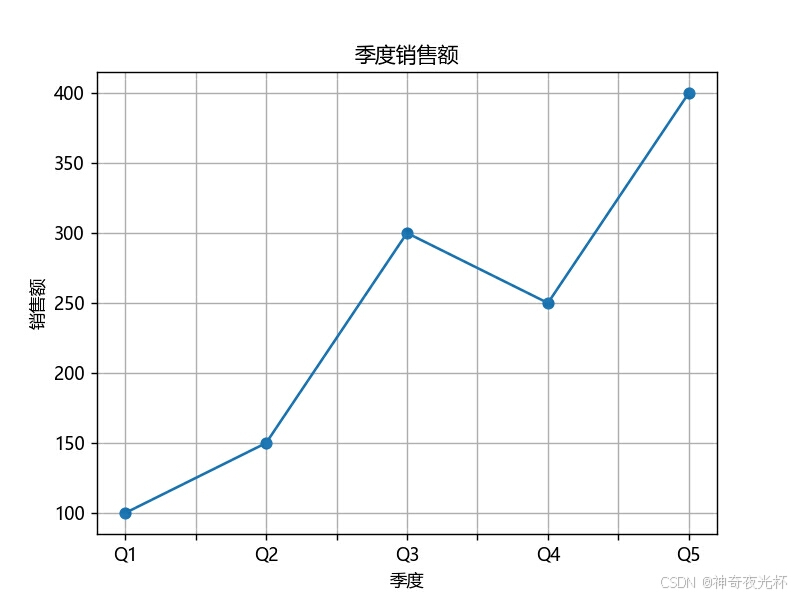
图21：

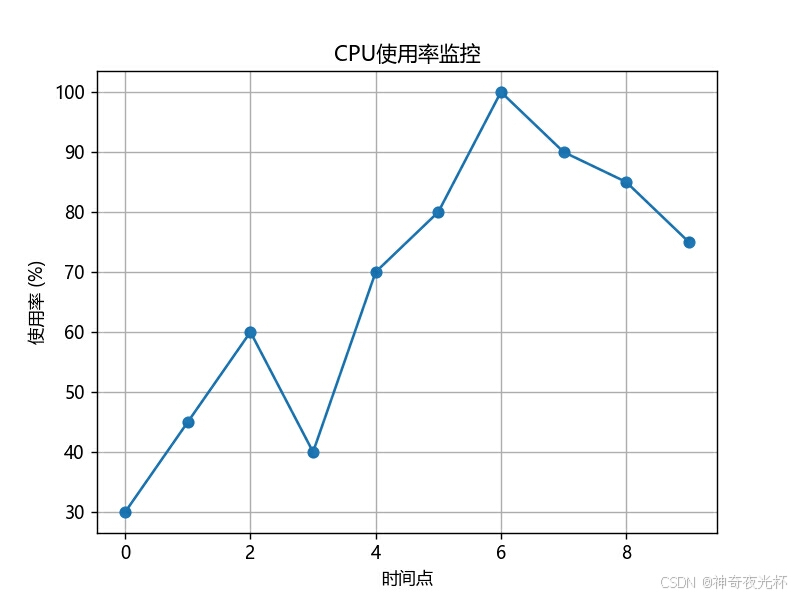
图22：

390、pandas.Series.plot.pie方法

390-1、语法

# 390、pandas.Series.plot.pie方法
pandas.Series.plot.pie(**kwargs)
Generate a pie plot.

A pie plot is a proportional representation of the numerical data in a column. This function wraps matplotlib.pyplot.pie() for the specified column. If no column reference is passed and subplots=True a pie plot is drawn for each numerical column independently.

Parameters:
y
int or label, optional
Label or position of the column to plot. If not provided, subplots=True argument must be passed.

**kwargs
Keyword arguments to pass on to DataFrame.plot().

Returns:
matplotlib.axes.Axes or np.ndarray of them
A NumPy array is returned when subplots is True.

390-2、参数

390-2-1、ax**(可选)****：**matplotlib.axes.Axes，如果指定，绘图将在此Axes对象上进行。

390-2-2、figsize**(可选)****：**元组，指定图形的宽度和高度，如(6, 6)。

390-2-3、labels**(可选)****：**array-like，指定饼图中各部分的标签，如果没有指定，将使用系列的索引。

390-2-4、colors**(可选)****：**array-like，自定义饼图中各部分的颜色。

390-2-5、autopct**(可选)****：**tr或callable，用于显示占比的格式字符串，如 '{:.1f}%'，或者自定义的格式化函数。

390-2-6、startangle**(可选)****：**float，饼图开始绘制的角度(以度为单位)。

390-2-7、shadow**(可选)****：**布尔值，是否在饼图上添加阴影。

390-2-8、explode**(可选)****：**array-like，指定各部分的"爆炸"参数，表示各部分与中心的距离，如[0.1, 0, 0, 0]表示第一部分向外移动。

390-2-9、radius**(可选)****：**float，饼图的半径。

390-2-10、counterclock**(可选)****：**布尔值，是否逆时针排列饼图的部分。

390-2-11、pctdistance**(可选)****：**float，标签与饼图中心的距离比例。

390-2-12、normalization**(可选)****：**布尔值，是否进行归一化展示(所有部分加起来为1)。

390-2-13、**kwargs**(可选)****：**其他关键字参数，传递给matplotlib的其他参数，例如title, xlabel, ylabel等。

390-3、功能

用于绘制饼图，显示系列中各个元素的相对大小，饼图通常用来展示分类数据的组成成分。

390-4、返回值

返回一个matplotlib.axes.Axes对象，允许在绘制饼图之后继续进行其他的图形修改。

390-5、说明

使用场景：

**390-5-1、市场份额分析：**在商业和市场分析中，可以用饼图展示各竞争对手的市场份额。例如，某个行业中不同品牌的销售额占比。

**390-5-2、预算分配：**在财务分析中，饼图可以用来展示公司预算的分配情况，例如各部门的预算占总预算的比例。

**390-5-3、社会调查结果：**在问卷调查或社会研究中，可以把受访者的选择或偏好展示成饼图，例如调查中不同选项的选择比例。

**390-5-4、产品成分成分占比：**在食品工业中，饼图可以展示产品中各成分的配比，例如某种饮料中不同成分的比例。

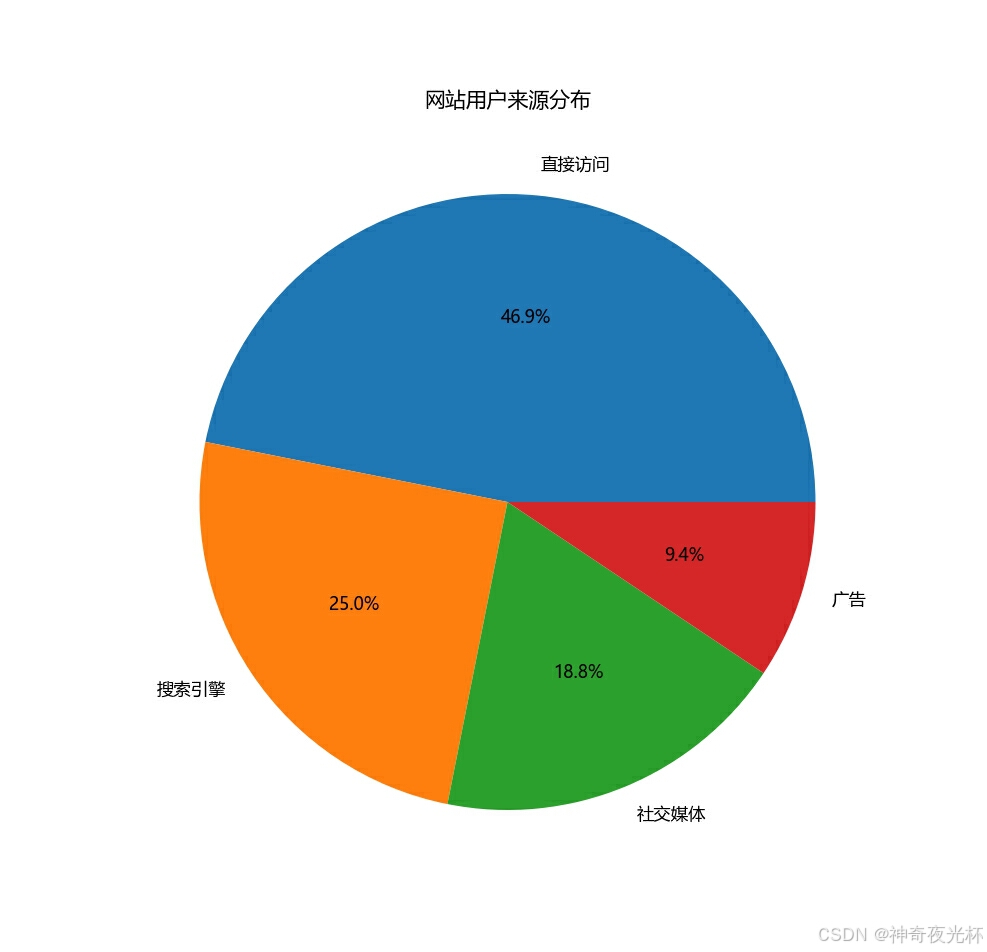
**390-5-5、用户行为分析：**在网站分析中，可以用饼图显示用户来源的比例，如直接访问、搜索引擎和社交媒体的用户分布。

**390-5-6、时间分配：**个人时间管理分析时，通过饼图展示在工作、学习、娱乐等项上花费的时间比例。

**390-5-7、投票结果：**在选举或民意调查中，饼图可以用来展示各候选人的得票比例，帮助直观理解选情。

390-6、用法

390-6-1、数据准备

无

390-6-2、代码示例

# 390、pandas.Series.plot.pie方法
# 390-1、市场份额分析
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib
# 配置字体，确保中文字符正常显示
matplotlib.rcParams['font.sans-serif'] = ['Microsoft YaHei']
matplotlib.rcParams['axes.unicode_minus'] = False  # 解决负号 '-' 显示问题
# 制造一个市场份额的数据
data = {'品牌': ['品牌A', '品牌B', '品牌C', '品牌D'], '市场份额': [30, 25, 20, 25]}
df = pd.DataFrame(data)
# 设置索引为品牌
df.set_index('品牌', inplace=True)
# 绘制饼图
df['市场份额'].plot.pie(autopct='%1.1f%%', figsize=(8, 8))
plt.title('市场份额分布')
plt.ylabel('')  # 不显示y轴的标签
plt.show()

# 390-2、预算分配
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib
# 配置字体，确保中文字符正常显示
matplotlib.rcParams['font.sans-serif'] = ['Microsoft YaHei']
matplotlib.rcParams['axes.unicode_minus'] = False  # 解决负号 '-' 显示问题
# 制造一个预算分配的数据
budget_data = {'部门': ['研发', '市场', '运营', '人事'], '预算': [40, 30, 20, 10]}
budget_df = pd.DataFrame(budget_data)
# 设置索引为部门
budget_df.set_index('部门', inplace=True)
# 绘制饼图
budget_df['预算'].plot.pie(autopct='%1.1f%%', figsize=(8, 8))
plt.title('公司预算分配')
plt.ylabel('')  # 不显示y轴的标签
plt.show()

# 390-3、社会调查结果
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib
# 配置字体，确保中文字符正常显示
matplotlib.rcParams['font.sans-serif'] = ['Microsoft YaHei']
matplotlib.rcParams['axes.unicode_minus'] = False  # 解决负号 '-' 显示问题
# 制造一个调查结果的数据
survey_data = {'选项': ['选项A', '选项B', '选项C'], '选择人数': [200, 150, 100]}
survey_df = pd.DataFrame(survey_data)
# 设置索引为选项
survey_df.set_index('选项', inplace=True)
# 绘制饼图
survey_df['选择人数'].plot.pie(autopct='%1.1f%%', figsize=(8, 8))
plt.title('调查选项选择比例')
plt.ylabel('')  # 不显示y轴的标签
plt.show()

# 390-4、产品成分占比
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib
# 配置字体，确保中文字符正常显示
matplotlib.rcParams['font.sans-serif'] = ['Microsoft YaHei']
matplotlib.rcParams['axes.unicode_minus'] = False  # 解决负号 '-' 显示问题
# 制造一个产品成分的数据
ingredient_data = {'成分': ['水', '糖', '果汁', '其他'], '占比': [60, 25, 10, 5]}
ingredient_df = pd.DataFrame(ingredient_data)
# 设置索引为成分
ingredient_df.set_index('成分', inplace=True)
# 绘制饼图
ingredient_df['占比'].plot.pie(autopct='%1.1f%%', figsize=(8, 8))
plt.title('饮料成分占比')
plt.ylabel('')  # 不显示y轴的标签
plt.show()

# 390-5、用户行为分析
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib
# 配置字体，确保中文字符正常显示
matplotlib.rcParams['font.sans-serif'] = ['Microsoft YaHei']
matplotlib.rcParams['axes.unicode_minus'] = False  # 解决负号 '-' 显示问题
# 制造一个用户来源的数据
user_data = {'来源': ['直接访问', '搜索引擎', '社交媒体', '广告'], '用户数': [1500, 800, 600, 300]}
user_df = pd.DataFrame(user_data)
# 设置索引为来源
user_df.set_index('来源', inplace=True)
# 绘制饼图
user_df['用户数'].plot.pie(autopct='%1.1f%%', figsize=(8, 8))
plt.title('网站用户来源分布')
plt.ylabel('')  # 不显示y轴的标签
plt.show()

390-6-3、结果输出

# 390、pandas.Series.plot.pie方法
# 390-1、市场份额分析
# 见图23

# 390-2、预算分配
# 见图24

# 390-3、社会调查结果
# 见图25

# 390-4、产品成分占比
# 见图26

# 390-5、用户行为分析
# 见图27

图23：

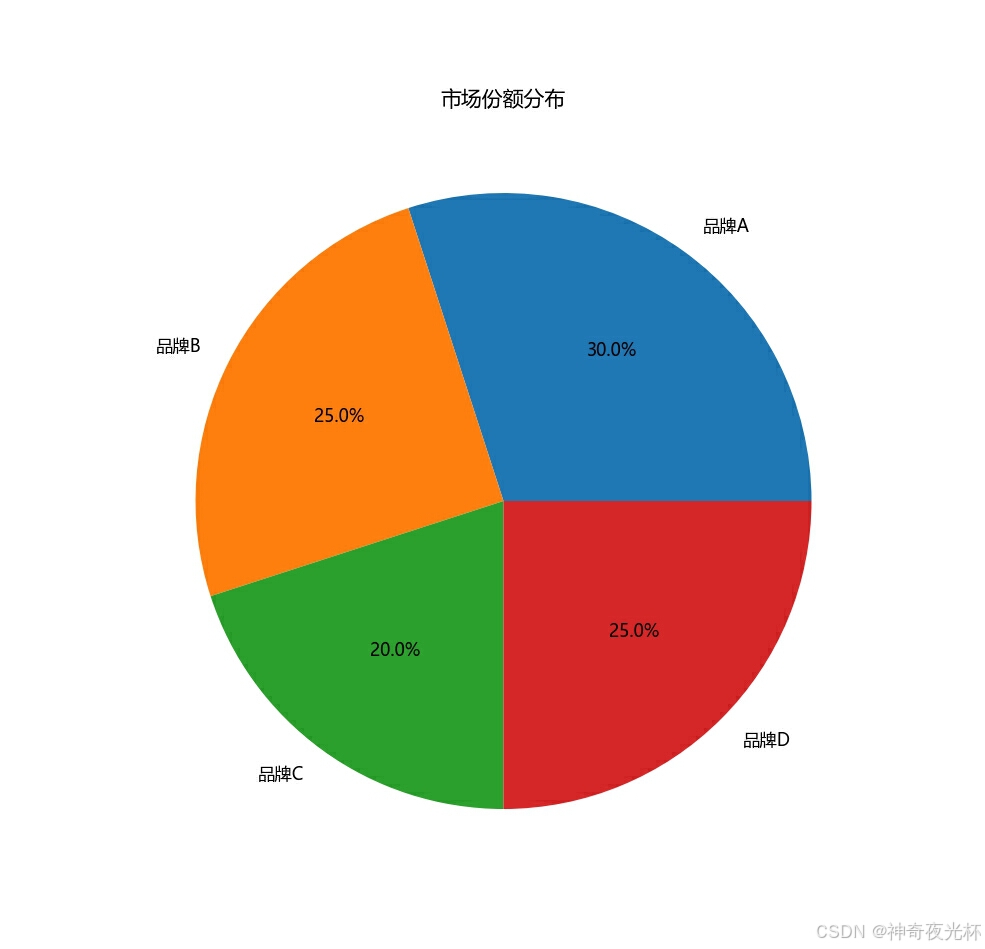
图24：

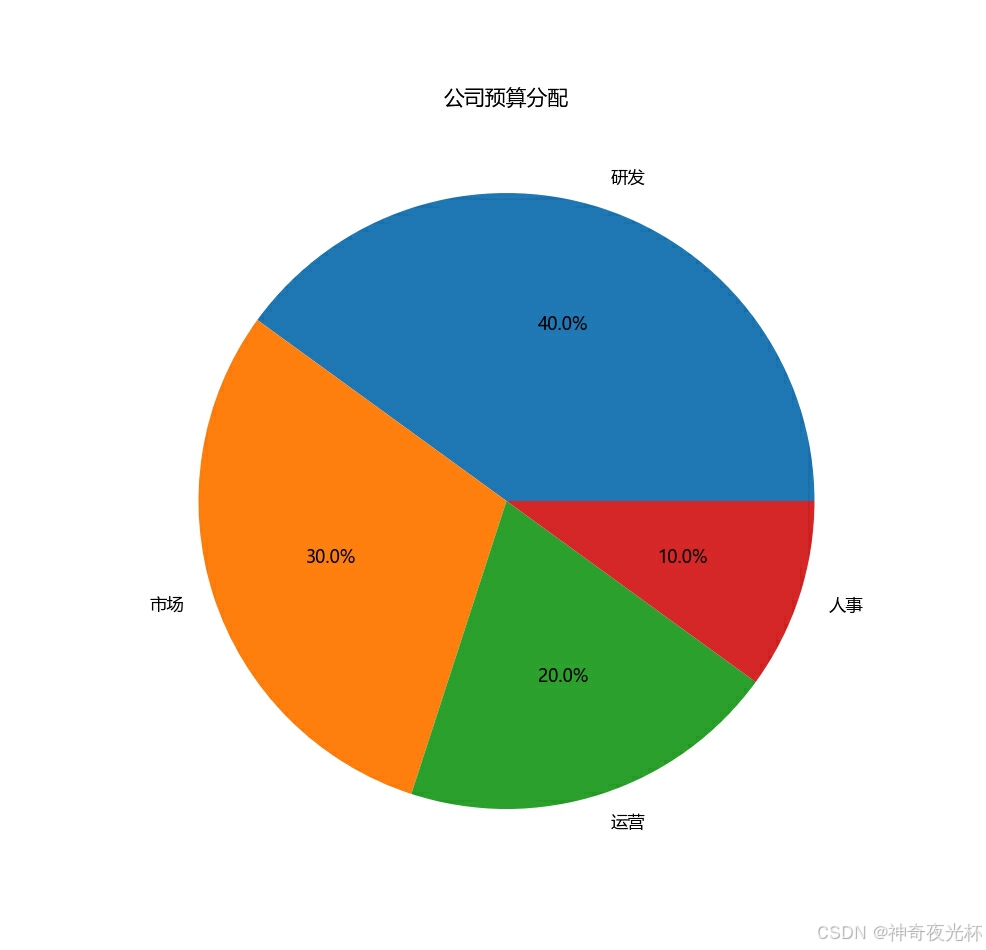
图25：

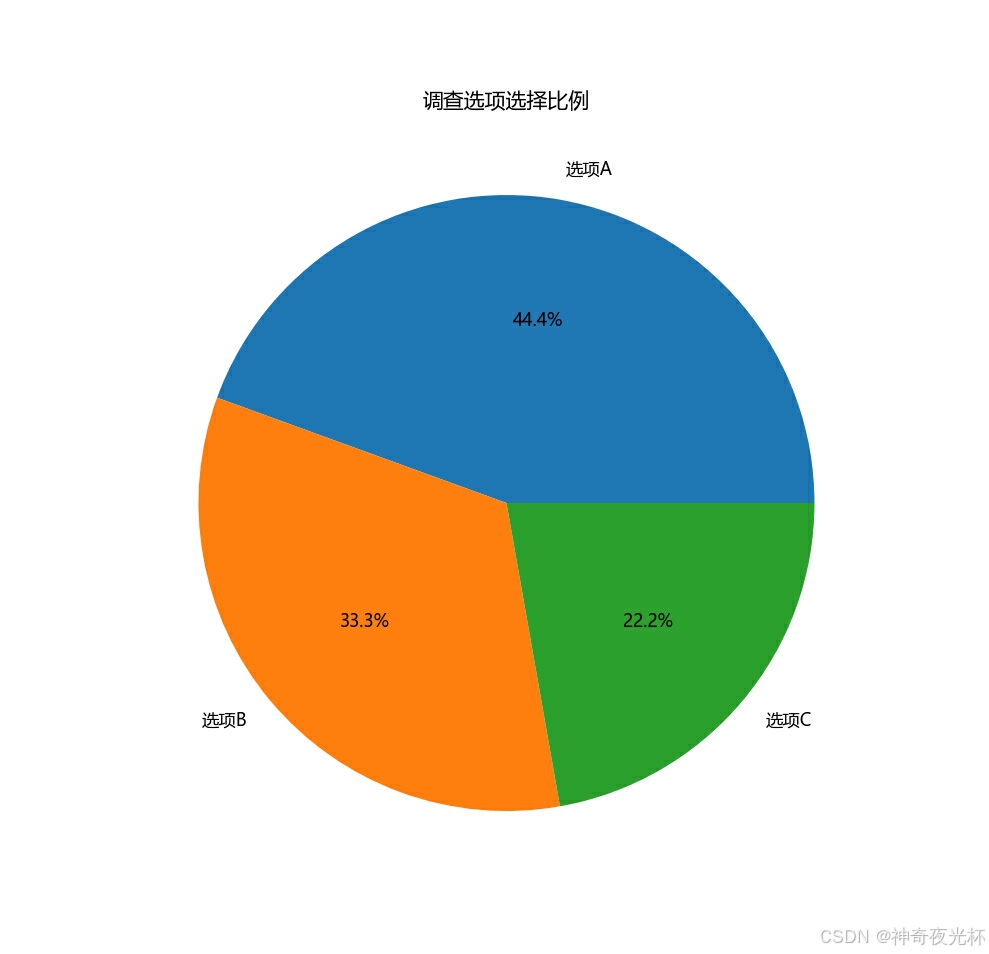
图26：

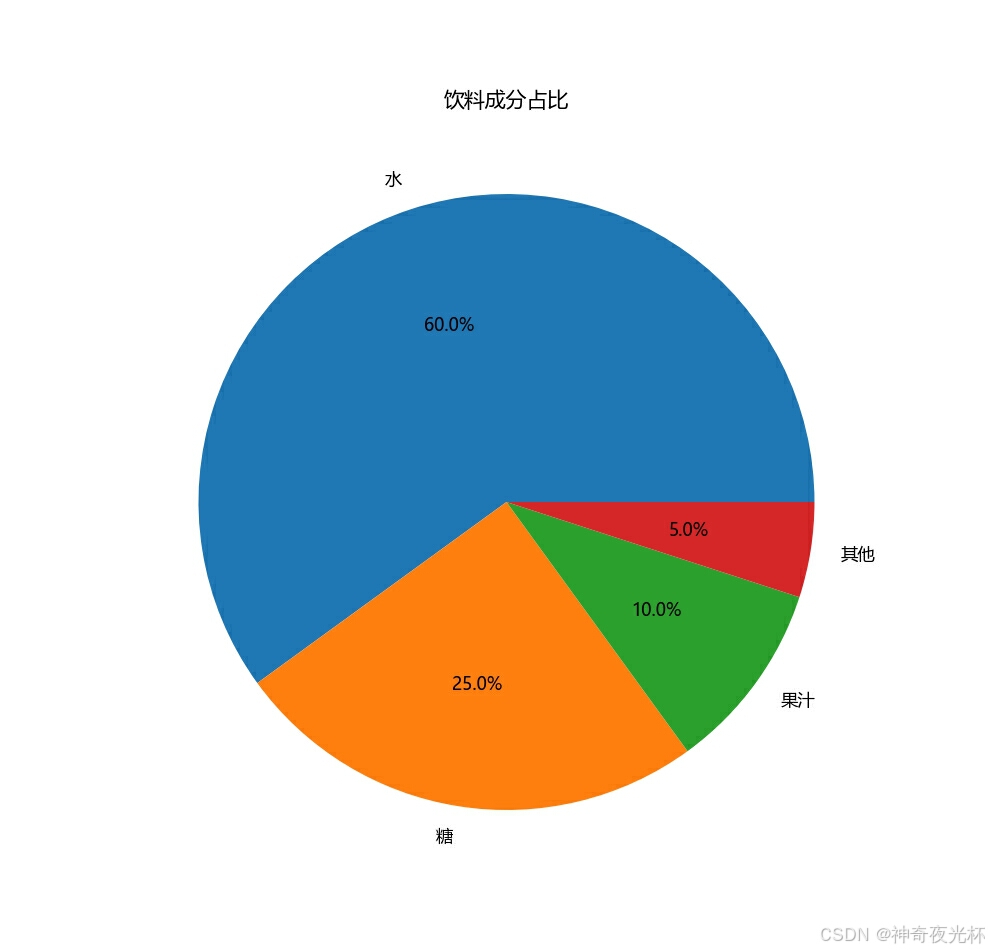
图27：

二、推荐阅读

1、Python筑基之旅

2、Python函数之旅

3、Python算法之旅

4、Python魔法之旅

5、博客个人主页