矩阵--旋转图像

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在**原地** 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。

示例：

复制代码

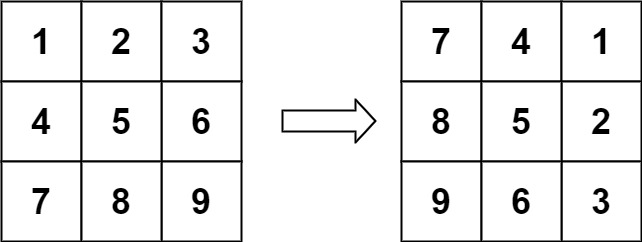
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

方法一：（测试只适用于3*3）

void rotate(vector<vector<int>>& matrix)
{
	int m = matrix.size(), n = matrix[0].size();
	if (m == 0 || n == 0)
	{
		return;
	}
	vector<vector<int> > new_matrix(m, vector<int>(n, 0));
	int right = n - 1, down = m - 1;
	for (int i = 0; i < m; ++i)
	{
		for (int j = 0; j < n; ++j)
		{
			if (i == 0)
			{
				new_matrix[j][i + down] = matrix[i][j];
			}
			else if (j == 0 && i == down)
			{
				new_matrix[j][i - down] = matrix[i][j];
			}
			else if (j > 0 && j < right && i == down)
			{
				new_matrix[j][i - down] = matrix[i][j];
			}
			else if (i == down && j == right)
			{
				new_matrix[j][i - down] = matrix[i][j];
			}
			else
			{
				new_matrix[j][i] = matrix[i][j];
			}
		}
	}

	
	for (int i = 0; i < m; ++i)
	{
		for (int j = 0; j < n; ++j)
		{
			cout << new_matrix[i][j] << " ";
		}
		cout << endl;
	}
}
//void Print(vector<vector<int>>& matrix)
//{
//	int m = matrix.size(), n = matrix[0].size();
//	for (int i = 0; i < m; ++i)
//	{
//		for (int j = 0; j < n; ++j)
//		{
//			cout << matrix[i][j] << " ";
//		}
//		cout << endl;
//	}
//}
int main()
{
	//vector<vector<int> > matrix = { {5, 1, 9, 11},{2, 4, 8, 10},{13, 3, 6, 7},{15, 14, 12, 16} };
	vector<vector<int>> matrix = { {1,2,3},{4,5,6},{7,8,9} };
	rotate(matrix);
	return 0;
}

方法二：

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) 
    {
        int n=matrix.size();
        auto matrix_new=matrix;
        for(int i=0;i<n;++i)
        {
            for(int j=0;j<n;++j)
            {
                matrix_new[j][n-i-1]=matrix[i][j];
            }
        }
        matrix=matrix_new;
    }
};