LeetCode //C - 329. Longest Increasing Path in a Matrix

329. Longest Increasing Path in a Matrix

Given an m x n integers matrix, return the length of the longest increasing path in matrix.

From each cell, you can either move in four directions: left, right, up, or down. You may not move diagonally or move outside the boundary (i.e., wrap-around is not allowed).

Example 1:

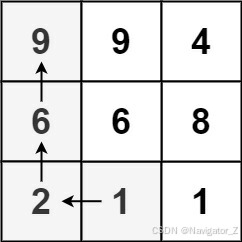
Input: matrix = $\[9,9,4$ , $6,6,8$ , $2,1,1$ ]
Output: 4
Explanation: The longest increasing path is $1, 2, 6, 9$ .

Example 2:

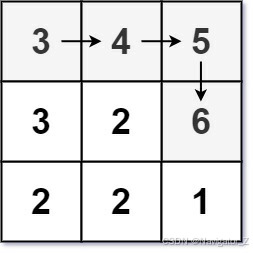
Input: matrix = $\[3,4,5$ , $3,2,6$ , $2,2,1$ ]
Output: 4
Explanation: The longest increasing path is $3, 4, 5, 6$ . Moving diagonally is not allowed.

Example 3:

Input: matrix = $\[1$ ]
Output: 1

Constraints:

m == matrix.length
n == matrix $i$ .length
1 <= m, n <= 200
0 < = m a t r i x $i$ $j$ < = 2 31 − 1 0 <= matrix $i$ $j$ <= 2^{31} - 1 0<=matrix $i$ $j$ <=231−1

From: LeetCode

Link: 329. Longest Increasing Path in a Matrix

Solution:

Ideas:

DFS with Memoization: The solution uses Depth-First Search (DFS) combined with memoization to explore all possible paths starting from each cell in the matrix.
Memoization: An array memo is used to store the length of the longest path starting from each cell to avoid redundant calculations.
Directions Array: The array directions stores the four possible directions (up, down, left, right) in which one can move.

Code:

c 复制代码

int dfs(int** matrix, int m, int n, int** memo, int i, int j) {
    if (memo[i][j] != 0) return memo[i][j];
    
    int directions[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
    int maxLength = 1;
    
    for (int d = 0; d < 4; d++) {
        int x = i + directions[d][0];
        int y = j + directions[d][1];
        
        if (x >= 0 && x < m && y >= 0 && y < n && matrix[x][y] > matrix[i][j]) {
            int len = 1 + dfs(matrix, m, n, memo, x, y);
            maxLength = (len > maxLength) ? len : maxLength;
        }
    }
    
    memo[i][j] = maxLength;
    return maxLength;
}

int longestIncreasingPath(int** matrix, int matrixSize, int* matrixColSize) {
    if (matrixSize == 0 || matrixColSize[0] == 0) return 0;
    
    int m = matrixSize;
    int n = matrixColSize[0];
    
    int** memo = (int**)malloc(m * sizeof(int*));
    for (int i = 0; i < m; i++) {
        memo[i] = (int*)calloc(n, sizeof(int));
    }
    
    int result = 0;
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            int len = dfs(matrix, m, n, memo, i, j);
            result = (len > result) ? len : result;
        }
    }
    
    for (int i = 0; i < m; i++) {
        free(memo[i]);
    }
    free(memo);
    
    return result;
}