AtCoder Beginner Contest 368（ABCDEFG题）视频讲解

A - Cut

Problem Statement

There is a stack of N N N cards, and the i i i-th card from the top has an integer A i A_i Ai written on it.

You take K K K cards from the bottom of the stack and place them on top of the stack, maintaining their order.

Print the integers written on the cards from top to bottom after the operation.

Constraints

KaTeX parse error: Expected 'EOF', got '&' at position 10: 1 \leq K &̲lt; N \leq 100
1 ≤ A i ≤ 100 1 \leq A_i \leq 100 1≤Ai≤100

All input values are integers.

Input

The input is given from Standard Input in the following format:

N N N K K K
A 1 A_1 A1 A 2 A_2 A2 ... \ldots ... A N A_N AN

Output

Let B i B_i Bi be the integer written on the i i i-th card from the top of the stack after the operation. Print B 1 , B 2 , ... , B N B_1,B_2,\ldots,B_N B1,B2,...,BN in this order, separated by spaces.

Sample Input 1

5 3
1 2 3 4 5

Sample Output 1

3 4 5 1 2

Initially, the integers written on the cards are 1 , 2 , 3 , 4 , 5 1,2,3,4,5 1,2,3,4,5 from top to bottom.

After taking three cards from the bottom of the stack and placing them on top, the integers written on the cards become 3 , 4 , 5 , 1 , 2 3,4,5,1,2 3,4,5,1,2 from top to bottom.

Sample Input 2

6 2
1 2 1 2 1 2

Sample Output 2

1 2 1 2 1 2

The integers written on the cards are not necessarily distinct.

Solution

具体见文末视频。

Code

cpp 复制代码

#include <bits/stdc++.h>
#define fi first
#define se second
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

signed main() {
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	int n, k;
	cin >> n >> k;
	std::vector<int> a(n + 1);
	for (int i = 1; i <= n; i ++)
		cin >> a[i];

	for (int i = n - k + 1; i <= n; i ++) cout << a[i] << " ";
	for (int i = 1; i <= n - k; i ++) cout << a[i] << " ";

	return 0;
}

B - Decrease 2 max elements

Problem Statement

You are given a sequence of N N N positive integers A = ( A 1 , A 2 , ... , A N ) A = (A_1, A_2, \dots ,A_N) A=(A1,A2,...,AN). Takahashi repeats the following operation until A A A contains one or fewer positive elements:

Sort A A A in descending order. Then, decrease both A 1 A_1 A1 and A 2 A_2 A2 by 1 1 1.

Find the number of times he performs this operation.

Constraints

2 ≤ N ≤ 100 2 \leq N \leq 100 2≤N≤100
1 ≤ A i ≤ 100 1 \leq A_i \leq 100 1≤Ai≤100

All input values are integers.

Input

The input is given from Standard Input in the following format:

N N N
A 1 A_1 A1 A 2 A_2 A2 ⋯ \cdots ⋯ A N A_N AN

Output

Print the answer.

Sample Input 1

4
1 2 3 3

Sample Output 1

The process goes as follows:

After the 1st operation, A A A is ( 2 , 2 , 2 , 1 ) (2, 2, 2, 1) (2,2,2,1).

After the 2nd operation, A A A is ( 1 , 1 , 2 , 1 ) (1, 1, 2, 1) (1,1,2,1).

After the 3rd operation, A A A is ( 1 , 0 , 1 , 1 ) (1, 0, 1, 1) (1,0,1,1).

After the 4th operation, A A A is ( 0 , 0 , 1 , 0 ) (0, 0, 1, 0) (0,0,1,0). A A A no longer contains more than one positive elements, so the process ends here.

Sample Input 2

3
1 1 100

Sample Output 2

Solution

具体见文末视频。

Code

cpp 复制代码

#include <bits/stdc++.h>
#define fi first
#define se second
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

signed main() {
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	int n;
	cin >> n;
	std::vector<int> a(n + 1);
	for (int i = 1; i <= n; i ++)
		cin >> a[i];

	int res = 0;
	while (1) {
		sort(a.begin() + 1, a.end(), greater<int>());
		if (a[2] == 0) {
			cout << res << endl;
			return 0;
		}
		a[1] --, a[2] --, res ++;
	};

	return 0;
}

C - Triple Attack

Problem Statement

You are playing a game.

There are N N N enemies lined up in a row, and the i i i-th enemy from the front has a health of H i H_i Hi.

You will repeat the following action until the healths of all enemies become 0 0 0 or less, using a variable T T T initialized to 0 0 0.

Increase T T T by 1 1 1. Then, attack the frontmost enemy with health 1 1 1 or more. If T T T is a multiple of 3 3 3, the enemy's health decreases by 3 3 3; otherwise, it decreases by 1 1 1.

Find the value of T T T when the healths of all enemies become 0 0 0 or less.

Constraints

1 ≤ N ≤ 2 × 1 0 5 1 \leq N \leq 2\times 10^5 1≤N≤2×105
1 ≤ H i ≤ 1 0 9 1 \leq H_i \leq 10^9 1≤Hi≤109

All input values are integers.

Input

The input is given from Standard Input in the following format:

N N N
H 1 H_1 H1 H 2 H_2 H2 ... \ldots ... H N H_N HN

Output

Print the answer.

Sample Input 1

3
6 2 2

Sample Output 1

The actions are performed as follows:
T T T becomes 1 1 1. Attack the 1st enemy, and its health becomes 6 − 1 = 5 6-1=5 6−1=5.
T T T becomes 2 2 2. Attack the 1st enemy, and its health becomes 5 − 1 = 4 5-1=4 5−1=4.
T T T becomes 3 3 3. Attack the 1st enemy, and its health becomes 4 − 3 = 1 4-3=1 4−3=1.
T T T becomes 4 4 4. Attack the 1st enemy, and its health becomes 1 − 1 = 0 1-1=0 1−1=0.
T T T becomes 5 5 5. Attack the 2nd enemy, and its health becomes 2 − 1 = 1 2-1=1 2−1=1.
T T T becomes 6 6 6. Attack the 2nd enemy, and its health becomes 1 − 3 = − 2 1-3=-2 1−3=−2.
T T T becomes 7 7 7. Attack the 3rd enemy, and its health becomes 2 − 1 = 1 2-1=1 2−1=1.
T T T becomes 8 8 8. Attack the 3rd enemy, and its health becomes 1 − 1 = 0 1-1=0 1−1=0.

Sample Input 2

9
1 12 123 1234 12345 123456 1234567 12345678 123456789

Sample Output 2

82304529

Sample Input 3

5
1000000000 1000000000 1000000000 1000000000 1000000000

Sample Output 3

3000000000

Beware of integer overflow.

Solution

具体见文末视频。

Code

cpp 复制代码

#include <bits/stdc++.h>
#define fi first
#define se second
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

signed main() {
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	int n;
	cin >> n;
	std::vector<int> a(n + 2, 0);
	for (int i = 1; i <= n; i ++)
		cin >> a[i];

	int res = 0, turn = 0;
	for (int i = 1; i <= n; i ++) {
		if (a[i] > 5) res += a[i] / 5 * 3, a[i] %= 5;
		while (a[i] > 0) {
			turn = (turn + 1) % 3;
			if (!turn) a[i] -= 3;
			else a[i] --;
			res ++;
		}
	}

	cout << res << endl;

	return 0;
}

D - Minimum Steiner Tree

Problem Statement

You are given a tree with N N N vertices numbered 1 1 1 to N N N. The i i i-th edge connects vertices A i A_i Ai and B i B_i Bi.

Consider a tree that can be obtained by removing some (possibly zero) edges and vertices from this graph. Find the minimum number of vertices in such a tree that includes all of K K K specified vertices V 1 , ... , V K V_1,\ldots,V_K V1,...,VK.

Constraints

1 ≤ K ≤ N ≤ 2 × 1 0 5 1 \leq K \leq N \leq 2\times 10^5 1≤K≤N≤2×105
1 ≤ A i , B i ≤ N 1 \leq A_i,B_i \leq N 1≤Ai,Bi≤N
KaTeX parse error: Expected 'EOF', got '&' at position 12: 1 \leq V_1 &̲lt; V_2 < \l...

The given graph is a tree.

All input values are integers.

Input

The input is given from Standard Input in the following format:

N N N K K K
A 1 A_1 A1 B 1 B_1 B1
⋮ \vdots ⋮
A N − 1 A_{N-1} AN−1 B N − 1 B_{N-1} BN−1
V 1 V_1 V1 ... \ldots ... V K V_K VK

Output

Print the answer.

Sample Input 1

Sample Output 1

The given tree is shown on the left in the figure below. The tree with the minimum number of vertices that includes all of vertices 1 , 3 , 5 1,3,5 1,3,5 is shown on the right.

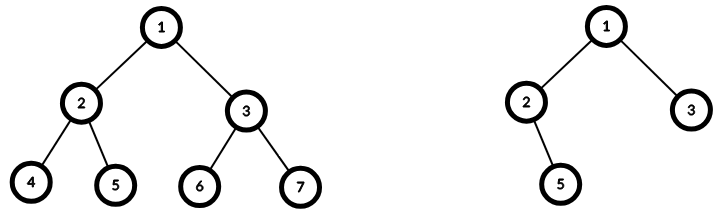
Sample Input 2

Sample Output 2

Sample Input 3

Sample Output 3

Solution

具体见文末视频。

Code

cpp 复制代码

#include <bits/stdc++.h>
#define fi first
#define se second
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

signed main() {
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	int n, k;
	cin >> n >> k;
	std::vector<vector<int>> g(n + 1);
	std::vector<int> ver(k + 1), st(n + 1, 0);
	for (int i = 1; i < n; i ++) {
		int u, v;
		cin >> u >> v;
		g[u].push_back(v), g[v].push_back(u);
	}
	for (int i = 1; i <= k; i ++) cin >> ver[i], st[ver[i]] |= 1;

	auto dfs = [&](auto self, int u, int fa) -> void {
		for (auto v : g[u]) {
			if (v == fa) continue;
			self(self, v, u), st[u] |= st[v];
		}
	};
	dfs(dfs, ver[1], -1);

	int res = 0;
	for (int i = 1; i <= n; i ++) res += st[i];

	cout << res << endl;

	return 0;
}

E - Train Delay

Problem Statement

In the nation of Atcoder, there are N N N cities numbered 1 1 1 to N N N, and M M M trains numbered 1 1 1 to M M M.

Train i i i departs from city A i A_i Ai at time S i S_i Si and arrives at city B i B_i Bi at time T i T_i Ti.

Given a positive integer X 1 X_1 X1, find a way to set non-negative integers X 2 , ... , X M X_2,\ldots,X_M X2,...,XM that satisfies the following condition with the minimum possible value of X 2 + ... + X M X_2+\ldots+X_M X2+...+XM.

Condition: For all pairs ( i , j ) (i,j) (i,j) satisfying 1 ≤ i , j ≤ M 1 \leq i,j \leq M 1≤i,j≤M, if B i = A j B_i=A_j Bi=Aj and T i ≤ S j T_i \leq S_j Ti≤Sj, then T i + X i ≤ S j + X j T_i+X_i \leq S_j+X_j Ti+Xi≤Sj+Xj.

In other words, for any pair of trains that are originally possible to transfer between, it is still possible to transfer even after delaying the departure and arrival times of each train i i i by X i X_i Xi.

It can be proved that such a way to set X 2 , ... , X M X_2,\ldots,X_M X2,...,XM with the minimum possible value of X 2 + ... + X M X_2+\ldots+X_M X2+...+XM is unique.

Constraints

2 ≤ N ≤ 2 × 1 0 5 2 \leq N \leq 2\times 10^5 2≤N≤2×105
2 ≤ M ≤ 2 × 1 0 5 2 \leq M \leq 2\times 10^5 2≤M≤2×105
1 ≤ A i , B i ≤ N 1 \leq A_i,B_i \leq N 1≤Ai,Bi≤N
A i ≠ B i A_i \neq B_i Ai=Bi
KaTeX parse error: Expected 'EOF', got '&' at position 12: 0 \leq S_i &̲lt; T_i \leq 10...
1 ≤ X 1 ≤ 1 0 9 1 \leq X_1 \leq 10^9 1≤X1≤109

All input values are integers.

Input

The input is given from Standard Input in the following format:

N N N M M M X 1 X_1 X1
A 1 A_1 A1 B 1 B_1 B1 S 1 S_1 S1 T 1 T_1 T1
⋮ \vdots ⋮
A M A_M AM B M B_M BM S M S_M SM T M T_M TM

Output

Print X 2 , ... , X M X_2,\ldots,X_M X2,...,XM that satisfy the condition with the minimum possible sum, in that order, separated by spaces.

Sample Input 1

Sample Output 1

0 10 0 0 5

The arrival of train 1 1 1 from city 1 1 1 to 2 2 2 is delayed by 15 15 15 and becomes time 35 35 35.

To allow transfer from train 1 1 1 to 3 3 3 in city 2 2 2, the departure of train 3 3 3 is delayed by 10 10 10, making it depart at time 35 35 35 and arrive at time 50 50 50.

Further, to allow transfer from train 3 3 3 to 6 6 6 in city 3 3 3, the departure of train 6 6 6 is delayed by 5 5 5, making it depart at time 50 50 50.

Other trains can operate without delay while still allowing transfers between originally transferable trains, so ( X 2 , X 3 , X 4 , X 5 , X 6 ) = ( 0 , 10 , 0 , 0 , 5 ) (X_2,X_3,X_4,X_5,X_6)=(0,10,0,0,5) (X2,X3,X4,X5,X6)=(0,10,0,0,5) satisfies the condition.

Moreover, there is no solution with a smaller sum that satisfies the condition, so this is the answer.

Sample Input 2

Sample Output 2

100 100 100 100 100 100 100 100

Sample Input 3

4 4 10
1 2 0 1
1 2 0 10
2 3 100 200
2 4 100 200

Sample Output 3

0 0 0

Solution

具体见文末视频。

Code

cpp 复制代码

#include <bits/stdc++.h>
#define fi first
#define se second
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

signed main() {
    cin.tie(0);
    cout.tie(0);
    ios::sync_with_stdio(0);

    int n, m, x;
    cin >> n >> m >> x;

    std::vector<array<int, 5>> tr(m + 1);
    std::vector<vector<PII>> S(n + 1);
    std::vector<int> res(m + 1);
    for (int i = 1; i <= m; i ++)
        cin >> tr[i][0] >> tr[i][1] >> tr[i][2] >> tr[i][3], tr[i][4] = i;

    sort(tr.begin() + 1, tr.end(), [&](auto a, auto b) {
        return a[3] < b[3];
    });
    for (int i = 1; i <= m; i ++) {
        if (tr[i][4] == 1) {
            res[1] = x;
            if (S[tr[i][1]].empty()) S[tr[i][1]].push_back({i, res[tr[i][4]] + tr[i][3]});
            else {
                int tmp = S[tr[i][1]].back().se;
                S[tr[i][1]].push_back({i, max(res[tr[i][4]] + tr[i][3], tmp)});
            }
            continue;
        }
        int lo = 0, ro = S[tr[i][0]].size() - 1, po = -1;
        while (lo <= ro) {
            int mid = lo + ro >> 1;
            if (tr[S[tr[i][0]][mid].fi][3] <= tr[i][2]) lo = mid + 1, po = mid;
            else ro = mid - 1;
        }
        if (~po) res[tr[i][4]] = max(S[tr[i][0]][po].se - tr[i][2], 0ll);
        if (S[tr[i][1]].empty()) S[tr[i][1]].push_back({i, res[tr[i][4]] + tr[i][3]});
        else {
            int tmp = S[tr[i][1]].back().se;
            S[tr[i][1]].push_back({i, max(res[tr[i][4]] + tr[i][3], tmp)});
        }
    }

    for (int i = 2; i <= m; i ++)
        cout << res[i] << " ";
    cout << endl;

    return 0;
}

Code of jiangly

cpp 复制代码

#include <bits/stdc++.h>

using i64 = long long;

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    
    int N, M, X0;
    std::cin >> N >> M >> X0;
    
    std::vector<int> A(M), B(M), S(M), T(M);
    for (int i = 0; i < M; i++) {
        std::cin >> A[i] >> B[i] >> S[i] >> T[i];
        A[i]--;
        B[i]--;
    }
    
    std::vector<std::array<int, 3>> e(2 * M);
    for (int i = 0; i < M; i++) {
        e[2 * i] = {S[i], 1, i};
        e[2 * i + 1] = {T[i], 0, i};
    }
    
    std::sort(e.begin(), e.end());
    
    std::vector<int> X(M);
    std::vector<int> tm(N);
    X[0] = X0;
    for (auto [t, o, i] : e) {
        if (o == 1) {
            X[i] = std::max(X[i], tm[A[i]] - S[i]);
        } else {
            tm[B[i]] = std::max(tm[B[i]], T[i] + X[i]);
        }
    }
    
    for (int i = 1; i < M; i++) {
        std::cout << X[i] << " \n"[i == M - 1];
    }
    
    return 0;
}

F - Dividing Game

Problem Statement

You are given a sequence of N N N positive integers A = ( A 1 , A 2 , ... , A N ) A = (A_1, A_2, \dots ,A_N) A=(A1,A2,...,AN), where each element is at least 2 2 2. Anna and Bruno play a game using these integers. They take turns, with Anna going first, performing the following operation.

Choose an integer i ( 1 ≤ i ≤ N ) i \ (1 \leq i \leq N) i (1≤i≤N) freely. Then, freely choose a positive divisor x x x of A i A_i Ai that is not A i A_i Ai itself, and replace A i A_i Ai with x x x.

The player who cannot perform the operation loses, and the other player wins. Determine who wins assuming both players play optimally for victory.

Constraints

1 ≤ N ≤ 1 0 5 1 \leq N \leq 10^5 1≤N≤105
2 ≤ A i ≤ 1 0 5 2 \leq A_i \leq 10^5 2≤Ai≤105

All input values are integers.

Input

The input is given from Standard Input in the following format:

N N N
A 1 A_1 A1 A 2 A_2 A2 ⋯ \cdots ⋯ A N A_N AN

Output

Print Anna if Anna wins the game, and Bruno if Bruno wins.

Sample Input 1

3
2 3 4

Sample Output 1

Anna

For example, the game might proceed as follows. Note that this example may not necessarily represent optimal play by both players:

Anna changes A 3 A_3 A3 to 2 2 2.

Bruno changes A 1 A_1 A1 to 1 1 1.

Anna changes A 2 A_2 A2 to 1 1 1.

Bruno changes A 3 A_3 A3 to 1 1 1.

Anna cannot operate on her turn, so Bruno wins.

Actually, for this sample, Anna always wins if she plays optimally.

Sample Input 2

4
2 3 4 6

Sample Output 2

Bruno

Solution

具体见文末视频。

Code

cpp 复制代码

#include <bits/stdc++.h>
#define fi first
#define se second
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

signed main() {
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	int n;
	cin >> n;
	std::vector<int> a(n + 1);
	std::vector<set<int>> S(100005);
	std::vector<int> sg(100005, 0);
	for (int i = 1; i <= n; i ++)
		cin >> a[i];

	for (int i = 1; i <= 100000; i ++) {
		for (int j = 0; j <= 100005; j ++)
			if (S[i].count(j)) sg[i] ++;
			else break;
		for (int j = i + i; j <= 100000; j += i)
			S[j].insert(sg[i]);
	}

	int res = 0;
	for (int i = 1; i <= n; i ++) {
		res ^= sg[a[i]];
	}

	if (!res) cout << "Bruno" << endl;
	else cout << "Anna" << endl;

	return 0;
}

G - Add and Multiply Queries

Problem Statement

You are given sequences of positive integers A A A and B B B of length N N N. Process Q Q Q queries given in the following forms in the order they are given. Each query is of one of the following three types.

Type 1 1 1: Given in the form 1 i x. Replace A i A_i Ai with x x x.

Type 2 2 2: Given in the form 2 i x. Replace B i B_i Bi with x x x.

Type 3 3 3: Given in the form 3 l r. Solve the following problem and print the answer.

Initially, set v = 0 v = 0 v=0. For i = l , l + 1 , . . . , r i = l, l+1, ..., r i=l,l+1,...,r in this order, replace v v v with either v + A i v + A_i v+Ai or v × B i v \times B_i v×Bi. Find the maximum possible value of v v v at the end.
It is guaranteed that the answers to the given type 3 3 3 queries are at most 1 0 18 10^{18} 1018.

Constraints

1 ≤ N ≤ 1 0 5 1 \leq N \leq 10^5 1≤N≤105
1 ≤ A i ≤ 1 0 9 1 \leq A_i \leq 10^9 1≤Ai≤109
1 ≤ B i ≤ 1 0 9 1 \leq B_i \leq 10^9 1≤Bi≤109
1 ≤ Q ≤ 1 0 5 1 \leq Q \leq 10^5 1≤Q≤105

For type 1 1 1 and 2 2 2 queries, 1 ≤ i ≤ N 1 \leq i \leq N 1≤i≤N.

For type 1 1 1 and 2 2 2 queries, 1 ≤ x ≤ 1 0 9 1 \leq x \leq 10^9 1≤x≤109.

For type 3 3 3 queries, 1 ≤ l ≤ r ≤ N 1 \leq l \leq r \leq N 1≤l≤r≤N.

For type 3 3 3 queries, the value to be printed is at most 1 0 18 10^{18} 1018.

Input

The input is given from Standard Input in the following format:

N N N
A 1 A_1 A1 A 2 A_2 A2 ⋯ \cdots ⋯ A N A_N AN
B 1 B_1 B1 B 2 B_2 B2 ⋯ \cdots ⋯ B N B_N BN
Q Q Q
q u e r y 1 query_1 query1
q u e r y 2 query_2 query2
⋮ \vdots ⋮
q u e r y Q query_Q queryQ

Here, q u e r y i query_i queryi is the i i i-th query, given in one of the following formats:

1 1 1 i i i x x x

2 2 2 i i i x x x

3 3 3 l l l r r r

Output

Let q q q be the number of type 3 3 3 queries. Print q q q lines. The i i i-th line should contain the answer to the i i i-th type 3 3 3 query.

Sample Input 1

Sample Output 1

12
7

For the first query, the answer is ( ( 0 + A 1 ) × B 2 ) × B 3 = 12 ((0 + A_1) \times B_2) \times B_3 = 12 ((0+A1)×B2)×B3=12.

For the third query, the answer is ( ( 0 + A 1 ) + A 2 ) + A 3 = 7 ((0 + A_1) + A_2) + A_3 = 7 ((0+A1)+A2)+A3=7.

Sample Input 2

6
65 32 12 5 8 312
4 1 3 15 16 2
6
3 2 6
3 1 5
1 5 6
2 4 9
3 2 6
3 3 5

Sample Output 2

Solution

具体见文末视频。

Code

cpp 复制代码

#include <bits/stdc++.h>
#define fi first
#define se second
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int N = 1e5 + 10;

int tr[N];

int lowbit(int x) {
    return x & -x;
}
void add(int x, int val) {
    for (int i = x; i < N; i += lowbit(i)) tr[i] += val;
}
int sum(int x) {
	if (!x) return 0;
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) res += tr[i];
    return res;
}

signed main() {
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	int n, q;
	cin >> n;
	std::vector<int> a(n + 1), b(n + 1), s(n + 1, 0);
	std::set<int> po;
	for (int i = 1; i <= n; i ++) {
		cin >> a[i], add(i, a[i]);
	}
	for (int i = 1; i <= n; i ++) {
		cin >> b[i];
		if (b[i] > 1) po.insert(i);
	}

	cin >> q;
	while (q -- ) {
		int op, i, x, l, r;
		cin >> op;
		if (op == 1) {
			cin >> i >> x;
			add(i, x - a[i]), a[i] = x;
		} else if (op == 2) {
			cin >> i >> x;
			if (b[i] > 1) po.erase(i);
			b[i] = x;
			if (b[i] > 1) po.insert(i);
		} else {
			cin >> l >> r;
			auto it = po.lower_bound(l);
			std::vector<int> ok;
			int mx = 0;
			for (; it != po.end() && (*it) <= r; it ++) ok.push_back(*it);
			int lst = l - 1;
			for (auto v : ok) {
				mx += sum(v - 1) - sum(lst);
				if (mx + a[v] > mx * b[v]) {
					mx += a[v];
				} else {
					mx *= b[v];
				}
				lst = v;
			}
			mx += sum(r) - sum(lst);
			cout << mx << endl;
		}
	}

	return 0;
}

视频题解

AtCoder Beginner Contest 368（A ~ G 题讲解）

最后祝大家早日