排序算法（冒泡、插入、选择、快排、归并）原理动画及Python、Java实现

[1 冒泡排序](#1 冒泡排序)
- [1.1 原理](#1.1 原理)
- [1.2 Python、Java实现](#1.2 Python、Java实现)
[2 插入排序](#2 插入排序)
- [2.1 原理](#2.1 原理)
- [2.2 Python、Java实现](#2.2 Python、Java实现)
[3 选择排序](#3 选择排序)
- [3.1 原理](#3.1 原理)
- [3.2 Python、Java实现](#3.2 Python、Java实现)
[4 快速排序](#4 快速排序)
- [4.1 原理](#4.1 原理)
- [4.2 Python](#4.2 Python)
[5 归并排序](#5 归并排序)
- [5.1 原理](#5.1 原理)
- [5.2 Python](#5.2 Python)

目前就总结这五种了，其它的后面看到了再弄。

1 冒泡排序

参考冒泡排序（详细图解分析+实现，小白一看就会）

1.1 原理

从序列的第一个元素开始，比较相邻两个元素，若顺序错误（如：从小到大排序时，前一个元素大于后一个元素），则交换位置。继续对下一对相邻元素执行相同的操作，直到序列的末尾。

核心：多趟排序，把最大的泡浮上来

每一轮排序的目的都是找到整个数组中最大的数并把它排在最后端，最后一个最大数不再比较移动。一轮一轮的比较，直到只剩下一个数时（完成了N趟的排序）这个排序就完成了，从而实现从小到大的排序。

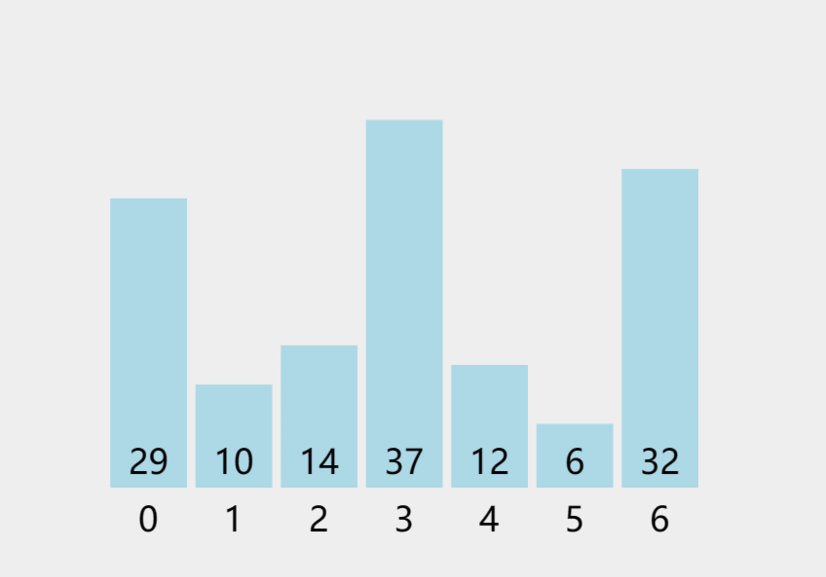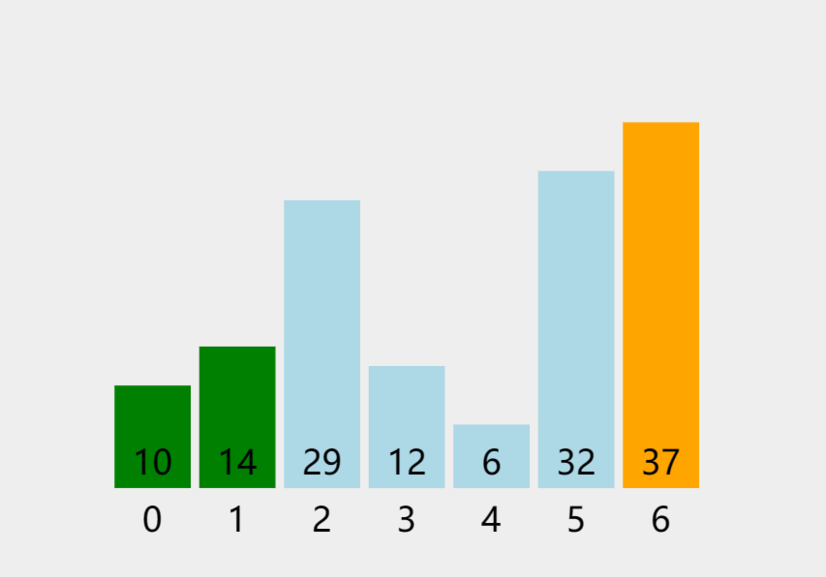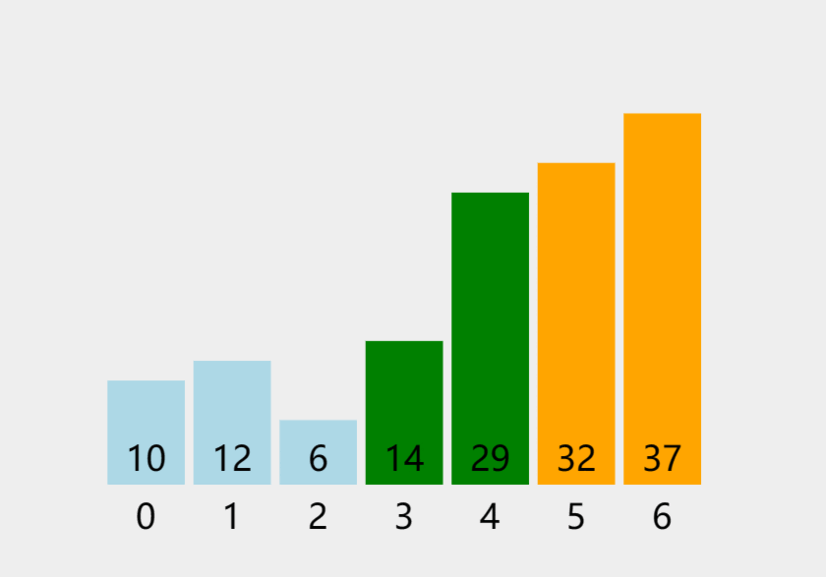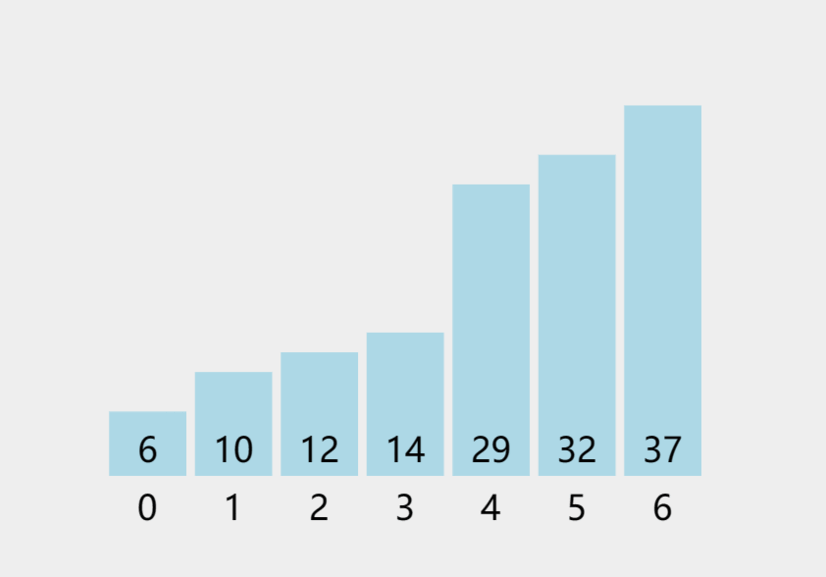
1.2 Python、Java实现

python 复制代码

def BubbleSort(nums):  # 从小到大
    n = len(nums)
    for i in range(n):  # 排序n轮
        for j in range(n - 1):  # 比较n-1组
            if nums[j] > nums[j + 1]:
                nums[j], nums[j + 1] = nums[j + 1], nums[j]
    return nums


nums = [29, 10, 14, 37, 12, 6, 32]
print(BubbleSort(nums))  # [6, 10, 12, 14, 29, 32, 37]

"""用一个标记优化"""
def BubbleSort(nums):  # 从小到大
    n = len(nums)
    for i in range(n):  # 排序n轮
        exchange = 0  # 标记是否进入排序循环
        for j in range(n - 1):  # 比较n-1组
            if nums[j] > nums[j + 1]:
                nums[j], nums[j + 1] = nums[j + 1], nums[j]
                exchange = 1
        # 如果前面的for循环都结束了，还没有一次交换，说明i后面已经完成了排序
        # 而前面的排序也已经在前面几轮中完成，所以可以直接跳出循环
        if exchange == 0:  
            break
    return nums


nums = [29, 10, 14, 37, 12, 6, 32]
print(BubbleSort(nums))  # [6, 10, 12, 14, 29, 32, 37]

java 复制代码

import java.util.Arrays;

public class Main {
    public static void main(String[] args) {
        int[] nums = {29, 10, 14, 37, 12, 6, 32};
        BubbleSort(nums);
//        System.out.println(nums);  // 这样会直接输出地址
        System.out.println(Arrays.toString(nums));  // 一开始想的是循环输出，这样后面的"]"前面还会有", "出现
        // [6, 10, 12, 14, 29, 32, 37]
    }

    /*
    如果函数被声明为static，它就可以被类直接调用，而不需要实例化类对象。
    如果函数没有被声明为static，它就必须通过实例化类对象来调用。
     */
    public static void BubbleSort(int[] nums){
        int n = nums.length;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n - 1; j++) {
                if (nums[j] > nums[j+1]) {
                    int temp = nums[j];
                    nums[j] = nums[j+1];
                    nums[j+1] = temp;
                }
            }
        }
    }

}

/*函数部分优化*/
    public static void BubbleSort(int[] nums){
        int n = nums.length;
        for (int i = 0; i < n; i++) {
            int exchange = 0;
            for (int j = 0; j < n - 1; j++) {
                if (nums[j] > nums[j+1]) {
                    int temp = nums[j];
                    nums[j] = nums[j+1];
                    nums[j+1] = temp;
                    exchange = 1;
                }
            }
            if (exchange == 0){
                break;
            }
        }
    }

时间复杂度：O(n^2)

是稳定的吗？

稳定指的是相同的数的相对位置是否改变，即5, 0, 9, 11, 9里面的两个9最后位置是否变化。冒泡排序是稳定的。 这一点在if nums[j] > nums[j + 1]中可以看出。

2 插入排序

十大排序算法（冒泡排序、插入排序、选择排序、希尔排序、堆排序、快排、归并排序、桶排序、计数排序、基数排序）

2.1 原理

就像是打扑克牌的摸牌过程，每从牌池里抽取一张牌，都会与手头已有的牌做比较，把它放在合适的位置。

描述：假设前n-1个元素已有序，现将第n个元素插入到前面已经排好的序列中，使得前n个元素有序，直到整个序列有序。一开始只能认为第一个元素是有序的，依次将其后面的元素插入到这个有序序列中来，直到整个序列有序为止。

2.2 Python、Java实现

python 复制代码

def InsertSort(nums):  # 从小到大
    n = len(nums)
    for i in range(1, n):  # 外部插入排序，默认第一个数有序，从第二个数开始排序
        if nums[i] < nums[i-1]:  # 现在这个数小于前面的数时，才进入排序过程（就好像拿到了大王直接往后面一放，不需要进入手中的牌进行排序）
            temp = nums[i]  # 记录这个要插入的数
            p = i-1  # 从前面一个开始比较
            while nums[p] > temp and p >= 0:  # 指针指的数如果大于要插入的数，就往后挪一位
                nums[p+1] = nums[p]
                p -= 1
            nums[p+1] = temp  # 结束循环时，p指向小于temp的数
    return nums


nums = [29, 10, 14, 37, 12, 6, 32]
print(InsertSort(nums))  # [6, 10, 12, 14, 29, 32, 37]

java 复制代码

import java.util.Arrays;

public class Main {
    public static void main(String[] args) {
        int[] nums = {29, 10, 14, 37, 12, 6, 32};
        InsertSort(nums);
//        System.out.println(nums);  // 这样会直接输出地址
        System.out.println(Arrays.toString(nums));  // 一开始想的是循环输出，这样后面的"]"前面还会有", "出现
        // [6, 10, 12, 14, 29, 32, 37]
    }

    public static void InsertSort(int[] nums){
        int n = nums.length;
        for (int i = 1; i < n; i++) {
            if (nums[i] < nums[i-1]){
                int temp = nums[i];
                int j;
                for (j = i-1; j >= 0 && nums[j] > temp; j--) {
                    /*
                    应该使用逻辑与符号 "&&" 而不是位与符号 "&"
                    因为逻辑与符号会在第一个条件不成立时直接跳出循环，而位与符号会继续执行第二个条件，可能导致数组越界异常
                     */
                    nums[j+1] = nums[j];
                }
                nums[j+1] = temp;
            }
        }
    }

}

时间复杂度：O(n^2)，最好是O(n)

插入排序是稳定的。 这一点在while nums[p] > temp可以看出。

3 选择排序

选择排序（详细图解分析+实现，小白一看就会）

3.1 原理

核心：多趟选择

内层循环中：

第一次在所有n个数里面找最小值，与第一个数交换；

第二次在后面n-1个数里面找最小值，与n-1个数里面的第一个数交换......

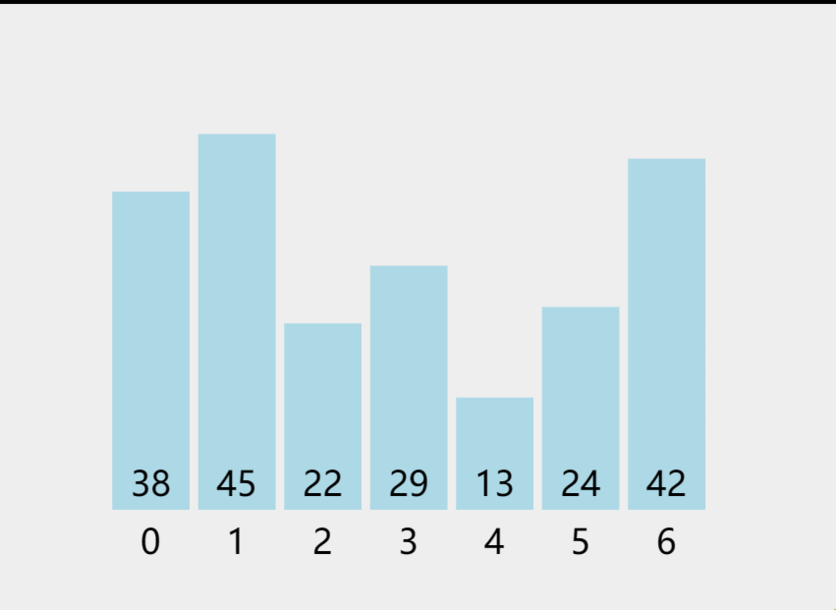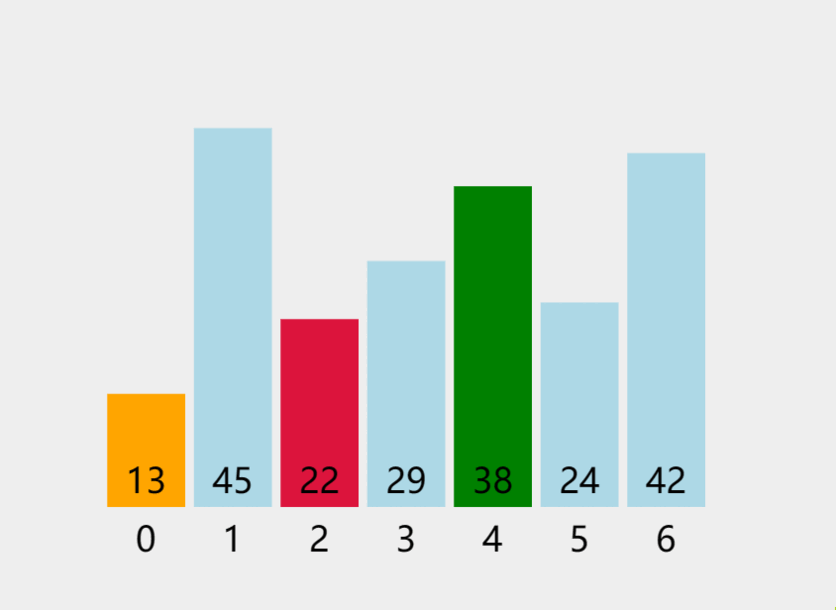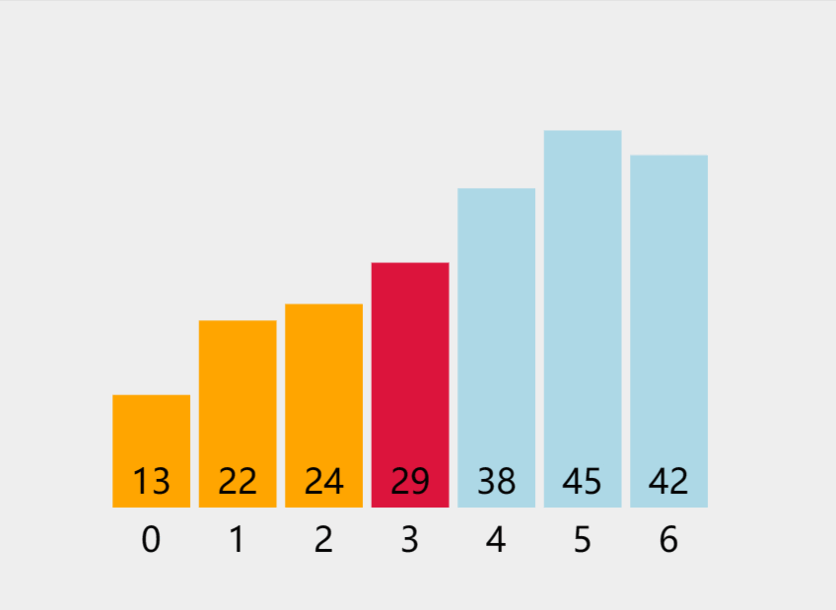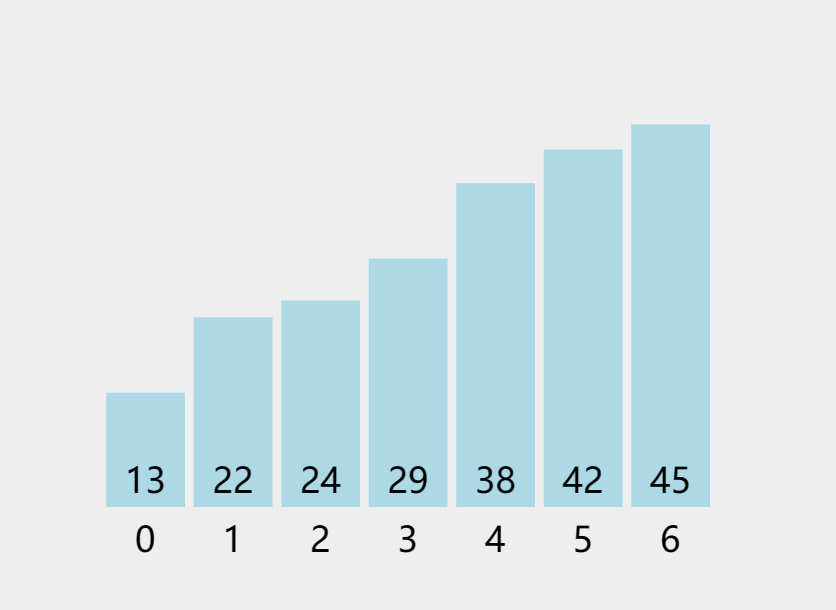
3.2 Python、Java实现

python 复制代码

def SelectSort(nums):  # 从小到大
    n = len(nums)
    for i in range(n):  # 排序n轮
        min_num = nums[i]
        min_index = i
        for j in range(i+1, n):
            if nums[j] < min_num:
                min_num = nums[j]
                min_index = j
        nums[i], nums[min_index] = nums[min_index], nums[i]

    return nums


nums = [29, 10, 14, 37, 12, 6, 32]
print(SelectSort(nums))  # [6, 10, 12, 14, 29, 32, 37]

java 复制代码

import java.util.Arrays;

public class Main {
    public static void main(String[] args) {
        int[] nums = {29, 10, 14, 37, 12, 6, 32};
        SelectSort(nums);
        System.out.println(Arrays.toString(nums));  // [6, 10, 12, 14, 29, 32, 37]
    }


    public static void SelectSort(int[] nums){
        int n = nums.length;
        for (int i = 0; i < n; i++) {
            int min_num = nums[i];
            int min_index = i;
            for (int j = i+1; j < n; j++) {
                if (nums[j] < min_num){
                    min_num = nums[j];
                    min_index = j;
                }
            }
            int temp = nums[i];
            nums[i] = nums[min_index];
            nums[min_index] = temp;
        }
    }

}

可以优化，设置成同时找最大值和最小值

时间复杂度：O(n^2)

选择排序是不稳定的。 因为发生了交换，如 3，3，2，2要和第一个3交换，则两个3就换了位置。

4 快速排序

【排序算法】快速排序（全坤式超详解）---------有这一篇就够啦

4.1 原理

分治思想：随机选一个pivot（一般是最左边或者最右边），然后比 pivot 小的放左边、大的放右边。

4.2 Python

用递归很快：

python 复制代码

def QuickSort(nums):  # 从小到大
    if len(nums) <= 1:
        return nums
    else:
        pivot = nums[0]
        left = [num for num in nums[1:] if num < pivot]
        right = [num for num in nums[1:] if num >= pivot]

        return QuickSort(left) + [pivot] + QuickSort(right)


nums = [29, 10, 14, 37, 12, 6, 32]
print(QuickSort(nums))  # [6, 10, 12, 14, 29, 32, 37]

Java版本就不写了。

左右指针法之类的其实也用了递归，这里不写了。能搜到好多。

时间复杂度：O(nlogn)，最坏情况是O(n^2)
不稳定。

5 归并排序

5.1 原理

同样是分治思想：

不断的分割数据，让数据的每一段都有序（一个数据相当于有序）

当所有子序列有序的时候，在把子序列归并，形成更大的子序列，最终整个数组有序。

核心：合并两个有序数组

5.2 Python

python 复制代码

def MergeSort(nums):  # 从小到大
    if len(nums) > 1:
        mid = len(nums) // 2  # 这里不能用 / 来除，会出现小数
        L = nums[:mid]
        R = nums[mid:]  # 递归到这里的时候，已经全部拆分成了长度为1的数组，也就是最底层

        # 递归
        MergeSort(L)
        MergeSort(R)

        # 到这一步的时候，其实就是开始从最底层处理，开始合并
        l = r = k = 0
        while l < len(L) and r < len(R):
            if L[l] <R[r]:
                nums[k] = L[l]
                l += 1
            else:
                nums[k] = R[r]
                r += 1
            k += 1

        # 左右数组长度可能不一样，所以还要检查是否还有剩余元素
        while l < len(L):  # 经过了上面，l按理来说应该正好等于len(L)了，如果还小于，说明有剩余的数
            nums[k] = L[l]
            l += 1
            k += 1
        while r < len(R):  # 经过了上面，l按理来说应该正好等于len(L)了，如果还小于，说明有剩余的数
            nums[k] = R[r]
            r += 1
            k += 1
            
    return nums


nums = [29, 10, 14, 37, 12, 6, 32]
print(MergeSort(nums))  # [6, 10, 12, 14, 29, 32, 37]

Java版本就不写了。

左右指针法之类的其实也用了递归，这里不写了。能搜到好多。

时间复杂度：O(nlogn)
稳定。

这几种就总结到这里了，其它堆排序之类的也都可以直接看十大排序算法（冒泡排序、插入排序、选择排序、希尔排序、堆排序、快排、归并排序、桶排序、计数排序、基数排序），接下来可以去牛客网刷题巩固了。

我的刷题笔记（包含答案解释）：排序算法刷题笔记【牛客网】