前面已经分别介绍了基于硬间隔最大化的线性可分支持向量机、基于软间隔最大化的线性支持向量机,这次来总结下使用核函数来解决非线性可分问题的非线性支持向量机。
一 非线性可分问题怎么解决
对于非线性可分问题,我们本着简化问题的思想,自然是希望将其转化为熟悉的线性可分问题进行处理,那么怎么做呢?对于一个在样本的原始空间中不是线性可分的数据,如下左图中的红色样本点和蓝色样本点,如果想要进行分类的话,可以将数据映射到更高维的特征空间中,如果映射的合适的话,就能找到一个超平面将数据分类,如下右图所示:
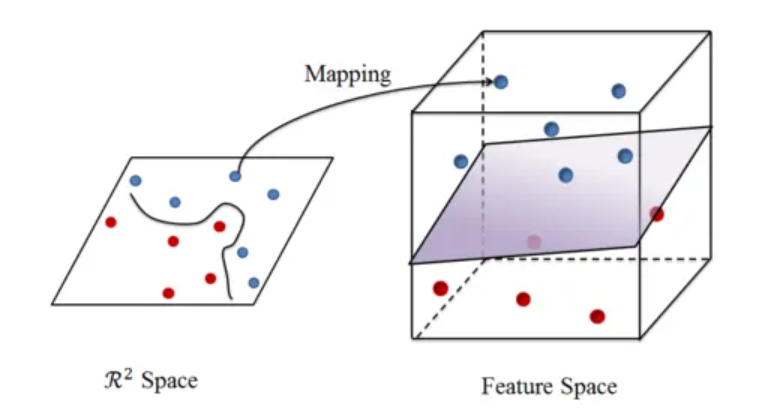
这种做法是特例还是可以普遍使用的呢?《机器学习》书上说:
如果原始空间是有限维,且属性数有限,那么一定存在一个高维特征空间使样本可分
不过书上并没有解释原因,我们先从低维直观的理解一下,如下图所示:在一维线性不可分的数据,可以映射成在二维线性可分的,在二维线性不可分的数据,可以映射成在三维线性可分的:
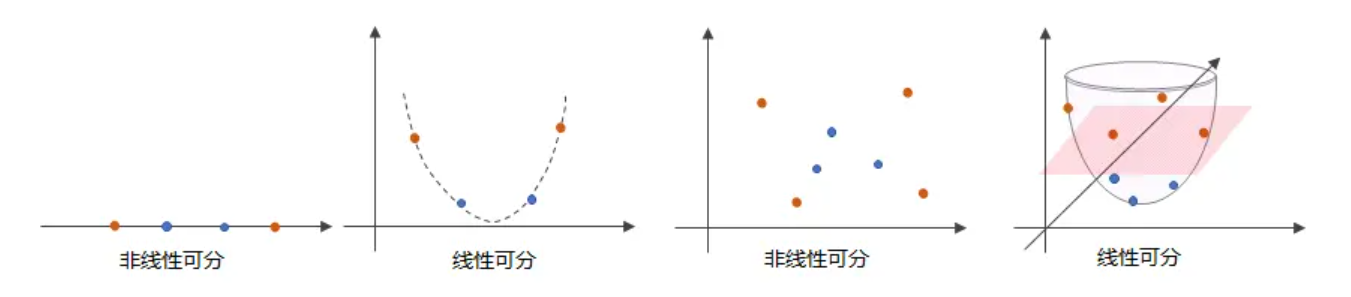
在更高的维度也适用吗?实际上,这个论点在理论上是有证明的,即Cover定理,Cover定理可以理解为:当空间的维数D越大时,在该空间的N个数据点间的线性可分的概率就越大。如果固定数据的数量N,维度D小于数据数量N时,特征空间维度越高,越有可能使数据线性可分;在维度超过数据数量时,数据一定线性可分(试想如果我们把每个数据点都映射到不同的坐标轴上,那么可不就是线性可分的了么)。
因此,我们对非线性可分的数据,可以将数据映射至高维空间,然后再用我们熟悉的线性分类器来分类,至此,剩下的问题就是怎么映射呢?这就需要核函数登场了。
二 核函数
2.1 什么是核函数
由于上述的超平面只能解决线性可分的问题,对于线性不可分的问题,例如:异或问题,我们需要使用核函数将其进行推广。一般地,解决线性不可分问题时,常常采用映射的方式,将低维原始空间映射到高维特征空间,使得数据集在高维空间中变得线性可分,从而再使用线性学习器分类。如果原始空间为有限维,即属性数有限,那么总是存在一个高维特征空间使得样本线性可分。若∅代表一个映射,则在特征空间中的划分函数变为:

按照同样的方法,先写出新目标函数的拉格朗日函数,接着写出其对偶问题,求L关于w和b的极大,最后运用SOM求解α。可以得出:
(1)原对偶问题变为:
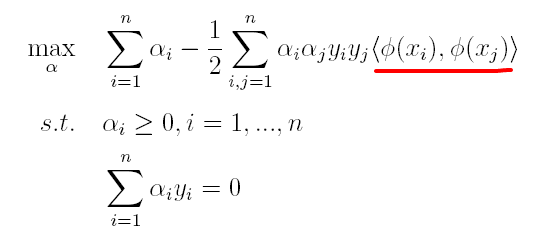
(2)原分类函数变为:
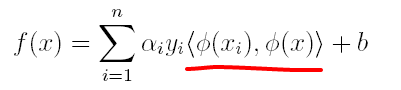
求解的过程中,只涉及到了高维特征空间中的内积运算,由于特征空间的维数可能会非常大,例如:若原始空间为二维,映射后的特征空间为5维,若原始空间为三维,映射后的特征空间将是19维,之后甚至可能出现无穷维,根本无法进行内积运算了,此时便引出了核函数(Kernel)的概念。

因此,核函数可以直接计算隐式映射到高维特征空间后的向量内积,而不需要显式地写出映射后的结果,它虽然完成了将特征从低维到高维的转换,但最终却是在低维空间中完成向量内积计算,与高维特征空间中的计算等效**(低维计算,高维表现)**,从而避免了直接在高维空间无法计算的问题。引入核函数后,原来的对偶问题与分类函数则变为:
(1)对偶问题:
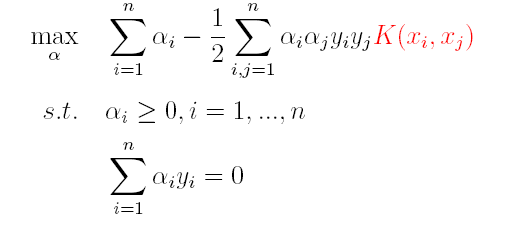
(2)分类函数:

因此,在线性不可分问题中,核函数的选择成了支持向量机的最大变数,若选择了不合适的核函数,则意味着将样本映射到了一个不合适的特征空间,则极可能导致性能不佳。同时,核函数需要满足以下这个必要条件:

2.2 常用核函数
由于核函数的构造十分困难,通常我们都是从一些常用的核函数中选择,下面列出了几种常用的核函数:

三 基于核函数的非线性支持向量机
因为在映射后的高维空间中,支持向量机还是在解决线性可分的数据,所以原理、目标函数什么的都跟之前是一样的,只是最终的形式上有所不同,最终可得非线性支持向量机模型:
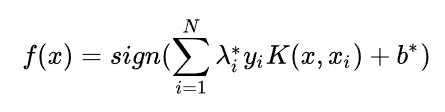
非线性支持向量机的算法过程:
