深度学习理论推导--梯度下降法

文章目录

• • 前言
  • 梯度示例
  • 微分推导
  • 梯度
  • 梯度下降法
  • 反向传播
  • [python 验证](#python 验证)
  • [均方差 MSE](#均方差 MSE)

当你迷茫的时候，请回头看看 目录大纲，也许有你意想不到的收获

前言

前面我们讲了推导了一元线性回归问题 与 多元线性回归问题 的求解，也就是当 残差平方和(RSS) 最小时，求解 参数 W 。

1. 一元线性函数：

y = w x + b y=wx+b y=wx+b

一元线性回归问题解法，最小二乘法：

w b \] = \[ ∑ i = 1 m x i 2 ∑ i = 1 m x i ∑ i = 1 m x i m \] − 1 \[ ∑ i = 1 m x i y i ∑ i = 1 m y i \] \\begin{bmatrix} w\\\\\[10pt\] b \\end{bmatrix} =\\begin{bmatrix} \\sum\\limits_{i=1}\^{m}{x_i}\^2 \& \\sum\\limits_{i=1}\^{m}{x_i} \\\\\[10pt\] \\sum\\limits_{i=1}\^{m}{x_i} \& m \\end{bmatrix}\^{-1} \\begin{bmatrix} \\sum\\limits_{i=1}\^{m}{x_i y_i}\\\\\[10pt\] \\sum\\limits_{i=1}\^{m}y_i \\end{bmatrix} wb = i=1∑mxi2i=1∑mxii=1∑mxim −1 i=1∑mxiyii=1∑myi 2. 多元线性函数： y = w 1 x 1 + w 2 x 2 + . . . + b y=w_1x_1+w_2x_2+...+b y=w1x1+w2x2+...+b 多元线性回归的解法，正规方程： W = ( X T X ) − 1 X T Y W=(X\^TX)\^{-1}X\^TY W=(XTX)−1XTY 其中，`一元线性函数`可以视为`特殊的多元函数`，也适合用多元线性回归的解法，并且上篇也已得证。 然而生活中的`大多函数都是非线性`，线性求解存在局限，因此需要一种通用求解的方法，那就是`梯度下降法`。 ### 梯度示例 来一个简单的函数 z = 1 ＋ x + 2 y z=1＋x+2y z=1＋x+2y 怎么理解呢？还是拿前面的主角小猪来举例吧，小猪开始重 1 斤，吃 1 碗饭长 1 斤肉，用 x 表示饭量，`纯吃饭`成长速度为 w 1 = 1 w_1=1 w1=1，吃 1 碗饲料长 2 斤肉，用 y 表示饲料量，`纯吃饲料`成长的速度为 w 2 = 2 w_2=2 w2=2，那么 z 表示小猪的重量。即： w 1 = ∂ z ∂ x = 1 w 2 = ∂ z ∂ y = 2 w_1=\\frac{\\partial{z}}{\\partial{x}}=1\\\\\[10pt\] w_2=\\frac{\\partial{z}}{\\partial{y}}=2\\\\\[10pt\] w1=∂x∂z=1w2=∂y∂z=2 可以这么说，z 的梯度是一个向量，我喜欢用 `列向量` 表示（ ∇ \\nabla ∇ 读作 nabla）： ∇ z = \[ ∂ z ∂ x ∂ z ∂ y \] = \[ w 1 w 2 \] \\nabla z =\\begin{bmatrix} \\frac{\\partial{z}}{\\partial{x}}\\\\\[10pt\] \\frac{\\partial{z}}{\\partial{y}} \\end{bmatrix} =\\begin{bmatrix} w_1\\\\\[10pt\] w_2 \\end{bmatrix} ∇z= ∂x∂z∂y∂z = w1w2 如果给它喂一碗东西（`饭与饲料混合物`），怎样才能让它长的最快呢？ 给我们的感觉是 `全喂饲料` 长的快啊！ 是的，相信自己感觉，没毛病。 但在微分领域中不太一样，还要考虑 `方向`，它改变了`加法的性质`（`平行四边形法则`），从而使增长比 `等量` 纯喂快，其实是在耍流氓，根本不是等量，早超过一碗的量了，下面我们就来手撕它！ ### 微分推导 在宏观中一碗太大了，增加一点都容易察觉出不一样，现在我们把这个碗缩小缩小，一直压缩到看不见，那这碗食量就是趋向于0。一个小碗的食量假如是 Δ r \\Delta r Δr： 1. 如果这个`小碗全装饭`，那么小猪吃后会长 Δ r \\Delta r Δr 斤肉； 2. 如果这个`小碗全装饲料`，那么小猪吃后会长 2 ⋅ Δ r 2\\cdot\\Delta r 2⋅Δr 斤肉； 到这里应该都没什么问题，也符合正常的成长速度。 好了，现在带上 `方向` 吧，现在有两个方向，一个是纯吃饭的方向(`x轴方向`)，一个是纯吃饲料的方向(`y轴方向`)，体重就是 `z 轴方向`，在直角坐标系中， z = 1 + x + 2 y z=1+x+2y z=1+x+2y 就是一个平面。 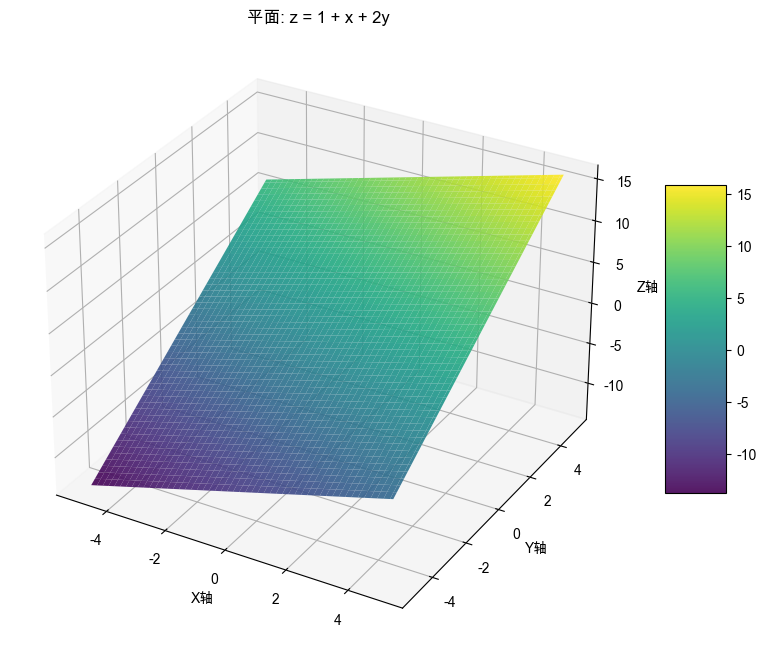 为了清晰统一,本文中带上箭头的表示`矢量(数值+方向)`,例如 Δ r ⃗ , Δ x ⃗ , Δ y ⃗ \\Delta \\vec{r},\\Delta \\vec{x},\\Delta \\vec{y} Δr ,Δx ,Δy ,没有的表示`标量(仅数值)`,例如 Δ z , Δ x , Δ y \\Delta z,\\Delta x,\\Delta y Δz,Δx,Δy。 现在初始小猪重1斤，位于O ( x 0 , y 0 , z 0 ) = ( 0 , 0 , 1 ) (x_0,y_0,z_0)=(0,0,1) (x0,y0,z0)=(0,0,1)，现在把 Δ r ⃗ \\Delta \\vec{r} Δr 分为两部分(都是`有方向`的向量)，一部分装饭 Δ x ⃗ \\Delta \\vec{x} Δx ，一部分装饲料 Δ y ⃗ \\Delta \\vec{y} Δy ， x ⃗ ⊥ y ⃗ \\vec{x}\\bot \\vec{y} x ⊥y ，那么就到了 P ( x 0 + Δ x , y 0 + Δ y , z 0 + Δ z ) (x_0+\\Delta x,y_0+\\Delta y,z_0+\\Delta z) (x0+Δx,y0+Δy,z0+Δz) 下面重点来了： Δ r ⃗ = Δ x ⃗ + Δ y ⃗ ∣ Δ r ∣ = ∣ Δ x ∣ 2 + ∣ Δ y ∣ 2 ∣ Δ r ∣ ≤ ∣ Δ x ∣ + ∣ Δ y ∣ \\Delta \\vec{r}= \\Delta \\vec{x} + \\Delta \\vec{y}\\\\\[10pt\] \|\\Delta r\|=\\sqrt{\|\\Delta x\|\^2+\|\\Delta y\|\^2}\\\\\[10pt\] \|\\Delta r\| \\le \|\\Delta x\| +\|\\Delta y\| Δr =Δx +Δy ∣Δr∣=∣Δx∣2+∣Δy∣2 ∣Δr∣≤∣Δx∣+∣Δy∣ 它满足`向量相加`（平行四边形相加），并不是普通的标量相加，模长满足`勾股定理`。 这里就是微观与宏观的不同，这也将导致我们在微观的结论与宏观不一样。 在`宏观`世界中，吃 `纯一碗饲料` 与吃 `一碗混合物` 相比，纯一碗饲料长的肉是最多的。 而在`微观`下，吃一碗 `饭与饲料混合物` 反而长的比 `纯一碗饲料` 要快，本质上就是因为微观上的`向量分解`，而且每个方向都相互垂直。有了 `方向` 就改变了加法的性质，其实是耍流氓，明明喂了 `超过一碗的食量`， ∣ Δ x ∣ + ∣ Δ y ∣ ≥ ∣ Δ r ∣ \|\\Delta x\| +\|\\Delta y\|\\ge\|\\Delta r\| ∣Δx∣+∣Δy∣≥∣Δr∣，愣是说满足 `平行四边形相加`，只喂了一碗 ∣ Δ r ∣ \|\\Delta r\| ∣Δr∣ 的量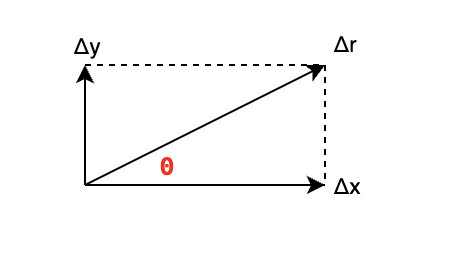！  它就是 `欺负你微观中看不出来`，所以小猪长的比纯喂一碗的快，就不足为奇了，下面我们就来推导一下吧！ 令小猪增长体重为 Δ z \\Delta z Δz，一小碗食量为 Δ r \\Delta r Δr，其中饭量为 Δ x \\Delta x Δx，饲料量为 Δ y \\Delta y Δy，这里 Δ z , Δ r , Δ x , Δ y \\Delta z ,\\Delta r, \\Delta x,\\Delta y Δz,Δr,Δx,Δy 都是`标量` 那么有如下关系： 全微分 : d z = ∂ z ∂ x d x + ∂ z ∂ y d y = d x + 2 d y 增量形式 : Δ z = z ( x 0 + Δ x , y 0 + Δ y ) − z ( x 0 , y 0 ) = 1 ⋅ Δ x + 2 ⋅ Δ y 全微分: dz=\\frac{\\partial{z}}{\\partial{x}}dx+\\frac{\\partial{z}}{\\partial{y}}dy=dx+2dy\\\\\[10pt\] 增量形式: \\Delta z= z(x_0+\\Delta x,y_0+\\Delta y)-z(x_0,y_0)\\\\\[10pt\] = 1\\cdot \\Delta x +2 \\cdot \\Delta y 全微分:dz=∂x∂zdx+∂y∂zdy=dx+2dy增量形式:Δz=z(x0+Δx,y0+Δy)−z(x0,y0)=1⋅Δx+2⋅Δy 因为 Δ x , Δ y 与 Δ r \\Delta x , \\Delta y 与 \\Delta r Δx,Δy与Δr 有勾股关系，所以令 Δ x = Δ r ⋅ cos ⁡ θ Δ y = Δ r ⋅ sin ⁡ θ \\Delta x=\\Delta r \\cdot \\cos \\theta \\\\\[10pt\] \\Delta y=\\Delta r \\cdot \\sin \\theta \\\\\[10pt\] Δx=Δr⋅cosθΔy=Δr⋅sinθ 则有 Δ z = 1 ⋅ Δ r cos ⁡ θ + 2 ⋅ Δ r sin ⁡ θ \\Delta z= 1 \\cdot \\Delta r \\cos \\theta +2 \\cdot \\Delta r \\sin \\theta Δz=1⋅Δrcosθ+2⋅Δrsinθ 令 sin ⁡ α = 1 1 + 2 2 = 1 5 cos ⁡ α = 2 1 + 2 2 = 2 5 tan ⁡ α = 1 2 \\sin \\alpha = \\frac{1}{\\sqrt{1+2\^2}}=\\frac{1}{\\sqrt{5}}\\\\\[10pt\] \\cos \\alpha = \\frac{2}{\\sqrt{1+2\^2}}=\\frac{2}{\\sqrt{5}}\\\\\[10pt\] \\tan \\alpha=\\frac{1}{2} sinα=1+22 1=5 1cosα=1+22 2=5 2tanα=21 上式可以化为 Δ z = 5 Δ r ⋅ ( sin ⁡ α cos ⁡ θ + cos ⁡ α sin ⁡ θ ) = 5 Δ r ⋅ sin ⁡ ( α + θ ) \\Delta z= \\sqrt{5} \\Delta r \\cdot (\\sin{\\alpha} \\cos{\\theta} +\\cos{\\alpha} \\sin{\\theta})\\\\\[10pt\] =\\sqrt{5}\\Delta r \\cdot \\sin{(\\alpha+\\theta)} Δz=5 Δr⋅(sinαcosθ+cosαsinθ)=5 Δr⋅sin(α+θ) 惊不惊喜？意不意外？死去的高中记忆瞬间活了过来！ Δ z \\Delta z Δz 有最大值，即: α + θ = π 2 Δ z m a x = 5 Δ r \\alpha+\\theta = \\frac{\\pi}{2}\\\\\[10pt\] \\Delta z_{max} =\\sqrt{5} \\Delta r α+θ=2πΔzmax=5 Δr 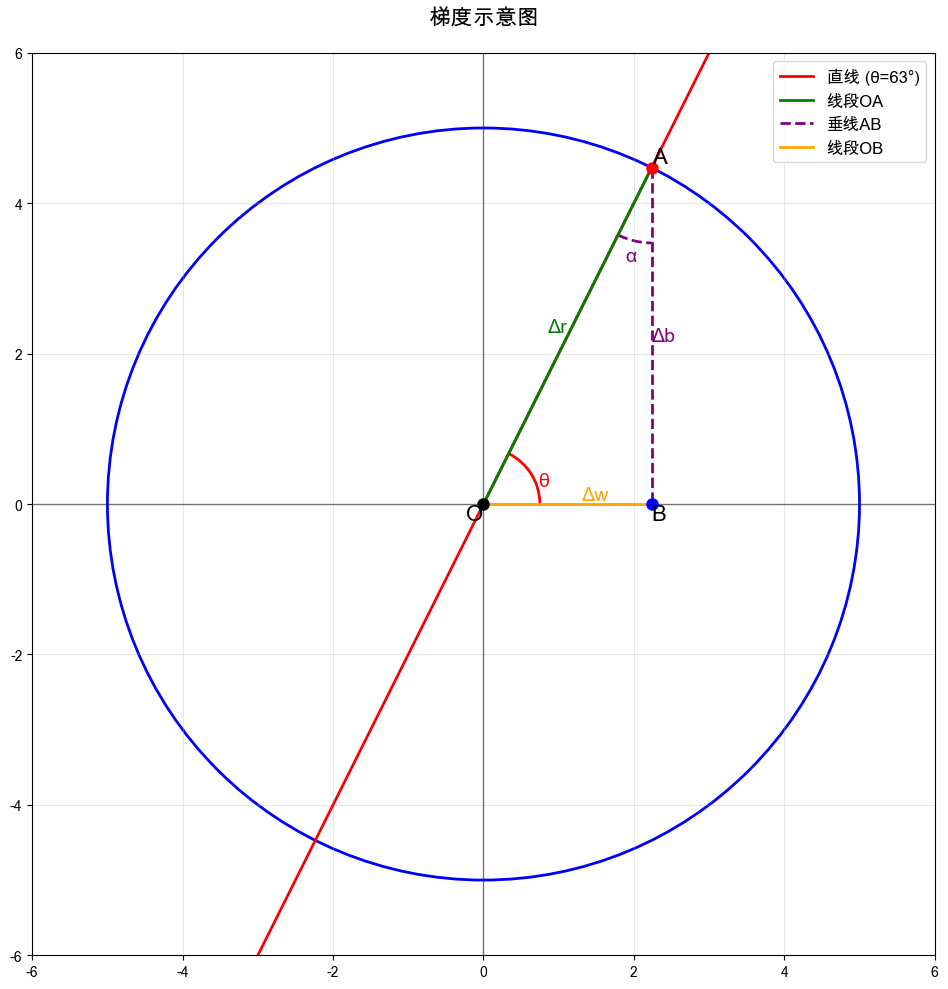 ### 梯度 这说明什么？ α \\alpha α 是已知角度（ tan ⁡ α = w 1 w 2 = 1 2 \\tan{\\alpha}=\\frac{w_1}{w_2}=\\frac{1}{2} tanα=w2w1=21），那么， Δ r ⃗ \\Delta \\vec{r} Δr 方向与向量 l ⃗ ( 1 , 2 ) \\vec{l}(1,2) l (1,2) 同向时， Δ z \\Delta z Δz 取到最大，且最大值为 5 Δ r \\sqrt{5}\\Delta r 5 Δr，列举几个值观察一下： | θ \\theta θ | 0 0 0 | π 6 \\frac{\\pi}{6} 6π | π 3 \\frac{\\pi}{3} 3π | π 2 \\frac{\\pi}{2} 2π | |---------------------------------------------------------------|------------------|--------------------------------------------------------------------------------------------|------------------------------------------------------------------------------------------------|------------------------| | Δ x = Δ r cos ⁡ θ \\Delta x=\\Delta r \\cos \\theta Δx=Δrcosθ | Δ r \\Delta r Δr | 3 2 Δ r \\frac{\\sqrt{3}}{2} \\Delta r 23 Δr | 1 2 Δ r \\frac{1}{2} \\Delta r 21Δr | 0 0 0 | | Δ y = Δ r sin ⁡ θ \\Delta y=\\Delta r \\sin \\theta Δy=Δrsinθ | 0 0 0 | 1 2 Δ r \\frac{1}{2}\\Delta r 21Δr | 3 2 Δ r \\frac{\\sqrt{3}}{2}\\Delta r 23 Δr | Δ r \\Delta r Δr | | Δ x + Δ y \\Delta x+\\Delta y Δx+Δy | Δ r \\Delta r Δr | 3 + 1 2 Δ r = 1.366 Δ r \\frac{\\sqrt{3}+1}{2}\\Delta r\\\\=1.366\\Delta r 23 +1Δr=1.366Δr | 1 + 3 2 Δ r = 1.366 Δ r \\frac{1+\\sqrt{3}}{2}\\Delta r\\\\=1.366\\Delta r 21+3 Δr=1.366Δr | Δ r \\Delta r Δr | | Δ z = Δ x + 2 Δ y \\Delta z=\\Delta x+2\\Delta y Δz=Δx+2Δy | Δ r \\Delta r Δr | 3 + 2 2 Δ r = 1.866 Δ r \\frac{\\sqrt{3}+2}{2}\\Delta r\\\\=1.866\\Delta r 23 +2Δr=1.866Δr | 1 + 2 3 2 Δ r = 2.232 Δ r \\frac{1+2\\sqrt{3}}{2}\\Delta r\\\\=2.232\\Delta r 21+23 Δr=2.232Δr | 2 Δ r 2\\Delta r 2Δr | 1. 喂的食量 ∣ Δ x ∣ + ∣ Δ y ∣ \|\\Delta x\|+\|\\Delta y\| ∣Δx∣+∣Δy∣ ≥ \\ge ≥ 一碗的量 ∣ Δ r ∣ \|\\Delta r\| ∣Δr∣ 2. 即使食量相同，得到的增量 Δ z \\Delta z Δz也不一定一样，例如纯一碗饭与纯一碗饲料，因为增长的方向不同 3. 改变 Δ x , Δ y \\Delta x,\\Delta y Δx,Δy 的大小比例，其实就在改变增长的方向，因为函数在方向上的导数不一样，因此结果增量 Δ z \\Delta z Δz也就不一定一样了 用向量的知识应该更容易理解： Δ z = Δ x + 2 Δ y = \[ ∂ z ∂ x ∂ z ∂ y \] \[ Δ x Δ y \] = \[ 1 2 \] \[ Δ x Δ y \] \\Delta z=\\Delta x+2\\Delta y\\\\\[10pt\] =\\begin{bmatrix} \\frac{\\partial{z}}{\\partial{x}}\&\\frac{\\partial{z}}{\\partial{y}} \\end{bmatrix} \\begin{bmatrix} \\Delta x \\\\\[10pt\] \\Delta y \\end{bmatrix}\\\\\[10pt\] =\\begin{bmatrix} 1\&2 \\end{bmatrix} \\begin{bmatrix} \\Delta x \\\\\[10pt\] \\Delta y \\end{bmatrix} Δz=Δx+2Δy=\[∂x∂z∂y∂z\] ΔxΔy =\[12\] ΔxΔy 这里梯度向量为 ∇ z ⃗ \\nabla \\vec{z} ∇z : ∇ z ⃗ = \[ ∂ z ∂ x ∂ z ∂ y \] = \[ 1 2 \] \\nabla \\vec{z}=\\begin{bmatrix} \\frac{\\partial{z}}{\\partial{x}}\\\\\[10pt\] \\frac{\\partial{z}}{\\partial{y}} \\end{bmatrix} =\\begin{bmatrix} 1\\\\\[10pt\] 2 \\end{bmatrix} ∇z = ∂x∂z∂y∂z = 12 而增量 Δ z \\Delta z Δz 就是两个向量 ∇ ⃗ ( 1 , 2 ) 与 Δ r ⃗ ( Δ x , Δ y ) \\vec{\\nabla} (1,2) 与 \\Delta \\vec{r}(\\Delta x,\\Delta y) ∇ (1,2)与Δr (Δx,Δy)的点积，只有当两个向量共线同向时，点积最大并且最大值为 5 Δ r = 5 ( Δ x ) 2 + ( Δ y ) 2 \\sqrt{5}\\Delta{r}=\\sqrt{5}\\sqrt{(\\Delta x)\^2+(\\Delta y)\^2} 5 Δr=5 (Δx)2+(Δy)2 也可以这样说: 在任意方向 l ⃗ \\vec{l} l ，沿着这个方向增长一个 Δ r ⃗ \\Delta \\vec{r} Δr ，等效向量分解成一个 Δ x ⃗ \\Delta \\vec{x} Δx 向量增长 与一个 Δ y ⃗ \\Delta \\vec{y} Δy 向量增长，那么 z 相应地增长一个 Δ z \\Delta z Δz，当这个方向 l ⃗ \\vec{l} l 刚好与 `梯度` 方向一致时，z 的增量 Δ z \\Delta z Δz 可以达到最大化，也就是小猪长的最快的时候饭与饲料比例混合。 针对于一个函数 y = f ( w 1 , w 2 , ... , b ) = w 1 x 1 + w 2 x 2 + . . . + b y=f(w_1,w_2,\\dots,b)=w_1x_1+w_2x_2+...+b y=f(w1,w2,...,b)=w1x1+w2x2+...+b 它的梯度为一个向量，用矩阵表示为： ∇ f ⃗ = \[ ∂ f ∂ w 1 ∂ f ∂ w 2 ... ∂ f ∂ w n ∂ f ∂ b \] \\nabla \\vec{f}=\\begin{bmatrix} \\frac{\\partial{f}}{\\partial{w_1}}\\\\\[10pt\] \\frac{\\partial{f}}{\\partial{w_2}}\\\\\[10pt\] \\dots\\\\\[10pt\] \\frac{\\partial{f}}{\\partial{w_n}}\\\\\[10pt\] \\frac{\\partial{f}}{\\partial{b}}\\\\\[10pt\] \\end{bmatrix} ∇f = ∂w1∂f∂w2∂f...∂wn∂f∂b∂f 对于高维的方向就只能靠想像了，但结论都是一样的，只要变量在 `梯度方向` 上增长一个单位，例如： Δ w \\Delta w Δw，这时 Δ f \\Delta f Δf 是最大的。 ### 梯度下降法 再回过头来看上面的示例： Δ z = 5 Δ r ⋅ ( sin ⁡ α cos ⁡ θ + cos ⁡ α sin ⁡ θ ) = 5 Δ r ⋅ sin ⁡ ( α + θ ) \\Delta z= \\sqrt{5} \\Delta r \\cdot (\\sin{\\alpha} \\cos{\\theta} +\\cos{\\alpha} \\sin{\\theta})\\\\\[10pt\] =\\sqrt{5}\\Delta r \\cdot \\sin{(\\alpha+\\theta)} Δz=5 Δr⋅(sinαcosθ+cosαsinθ)=5 Δr⋅sin(α+θ) Δ z \\Delta z Δz 也有最小值，即: α + θ = 3 π 2 Δ z m i n = − 5 Δ r \\alpha+\\theta = \\frac{3\\pi}{2}\\\\\[10pt\] \\Delta z_{min} =-\\sqrt{5} \\Delta r α+θ=23πΔzmin=−5 Δr 也就是变量在 `梯度相反方向` 上增长一个单位 Δ w \\Delta w Δw，这时 Δ f \\Delta f Δf 是最小的，也就是下降最快的，这就是 `梯度下降` 的原理。 就像爬山，沿着 `陡峭悬崖` 爬上山顶用时最短，调个头，沿悬崖下山也是最快的。 再比如我们刚才的小猪，按照某种比例（1饭：2饲料）给它增加食量它长的最快，那我反过来按这个比例从中减少食量，那就是减肥就最明显的。 像 RSS 这种求 `最小残差平方和` 的，就非常适合用梯度下降法来求解，目标是尽可能快速找到抛物面的 `谷底`。 用之前小猪的例子，w，b 是未知，需要根据样本数据来求的，假设满足如下函数： y = w x + b y=wx+b y=wx+b RSS 公式： R S S = ∑ i = 1 m ( y i \^ − y i ) 2 RSS=\\sum\\limits_{i=1}\^{m}{(\\hat{y_i}-y_i)\^2}\\\\\[10pt\] RSS=i=1∑m(yi\^−yi)2 为了求导方便，令: E = 1 2 R S S = 1 2 ∑ i = 1 m ( y i \^ − y i ) 2 E=\\frac{1}{2}{RSS}=\\frac{1}{2}\\sum\\limits_{i=1}\^{m}{(\\hat{y_i}-y_i)\^2}\\\\\[10pt\] E=21RSS=21i=1∑m(yi\^−yi)2 前面我们已经求出: ∂ E ∂ w = ∑ i = 1 m x i ( y i \^ − y i ) ∂ E ∂ b = ∑ i = 1 m ( y i \^ − y i ) \\frac{\\partial{E}}{\\partial{w}}=\\sum\\limits_{i=1}\^{m}x_i(\\hat{y_i}-y_i)\\\\\[10pt\] \\frac{\\partial{E}}{\\partial{b}}=\\sum\\limits_{i=1}\^{m}(\\hat{y_i}-y_i) ∂w∂E=i=1∑mxi(yi\^−yi)∂b∂E=i=1∑m(yi\^−yi) 那么 E 的梯度为： ∇ E ⃗ = \[ ∂ E ∂ w ∂ E ∂ b \] \[ ∑ i = 1 m x i ( y i \^ − y i ) ∑ i = 1 m ( y i \^ − y i ) \] \\nabla \\vec{E}=\\begin{bmatrix} \\frac{\\partial{E}}{\\partial{w}}\\\\\[10pt\] \\frac{\\partial{E}}{\\partial{b}} \\end{bmatrix}\\begin{bmatrix} \\sum\\limits_{i=1}\^{m}x_i(\\hat{y_i}-y_i)\\\\\[10pt\] \\sum\\limits_{i=1}\^{m}(\\hat{y_i}-y_i) \\end{bmatrix} ∇E = ∂w∂E∂b∂E i=1∑mxi(yi\^−yi)i=1∑m(yi\^−yi) 按照梯度的方向下降一个增量为 Δ r \\Delta r Δr，那么向量分解到 w 方向上的增量为 Δ w \\Delta w Δw，分解到 b 方向上的增量为 Δ b \\Delta b Δb，三者有勾股关系 ∣ Δ r ∣ 2 = ∣ Δ w ∣ 2 + ∣ Δ b ∣ 2 ∣ Δ w ∣ = ∣ Δ r ∣ cos ⁡ θ ∣ Δ b ∣ = ∣ Δ r ∣ sin ⁡ θ \|\\Delta r\|\^2=\\sqrt{\|\\Delta w\|\^2+\|\\Delta b\|\^2}\\\\\[10pt\] \|\\Delta w\|=\|\\Delta r\|\\cos \\theta\\\\\[10pt\] \|\\Delta b\|=\|\\Delta r\|\\sin \\theta\\\\\[10pt\] ∣Δr∣2=∣Δw∣2+∣Δb∣2 ∣Δw∣=∣Δr∣cosθ∣Δb∣=∣Δr∣sinθ 其中， θ \\theta θ 是可以根据样本量求得的： tan ⁡ θ = ∂ E ∂ b ∂ E ∂ w = ∑ i = 1 m ( y i \^ − y i ) ∑ i = 1 m x i ( y i \^ − y i ) θ = arctan ⁡ ∑ i = 1 m ( y i \^ − y i ) ∑ i = 1 m x i ( y i \^ − y i ) cos ⁡ θ = ∂ E ∂ w ( ∂ E ∂ w ) 2 + ( ∂ E ∂ b ) 2 = ∑ i = 1 m x i ( y i \^ − y i ) ( ∑ i = 1 m x i ( y i \^ − y i ) ) 2 + ( ∑ i = 1 m ( y i \^ − y i ) ) 2 sin ⁡ θ = ∂ E ∂ b ( ∂ E ∂ w ) 2 + ( ∂ E ∂ b ) 2 = ∑ i = 1 m ( y i \^ − y i ) ( ∑ i = 1 m x i ( y i \^ − y i ) ) 2 + ( ∑ i = 1 m ( y i \^ − y i ) ) 2 % tan \\tan \\theta=\\frac{\\frac{\\partial{E}}{\\partial{b}}}{\\frac{\\partial{E}}{\\partial{w}}} =\\frac{\\sum\\limits_{i=1}\^{m}(\\hat{y_i}-y_i)}{\\sum\\limits_{i=1}\^{m}x_i(\\hat{y_i}-y_i)}\\\\\[10pt\] \\theta= \\arctan{\\frac{\\sum\\limits_{i=1}\^{m}(\\hat{y_i}-y_i)}{\\sum\\limits_{i=1}\^{m}x_i(\\hat{y_i}-y_i)}}\\\\\[10pt\] % cos \\cos \\theta=\\frac{\\frac{\\partial{E}}{\\partial{w}}}{\\sqrt{(\\frac{\\partial{E}}{\\partial{w}})\^2+(\\frac{\\partial{E}}{\\partial{b}})\^2}}\\\\\[10pt\] =\\frac{\\sum\\limits_{i=1}\^{m}x_i(\\hat{y_i}-y_i)}{\\sqrt{({\\sum\\limits_{i=1}\^{m}x_i(\\hat{y_i}-y_i)})\^2+(\\sum\\limits_{i=1}\^{m}(\\hat{y_i}-y_i))\^2}}\\\\\[10pt\] % sin \\sin \\theta=\\frac{\\frac{\\partial{E}}{\\partial{b}}}{\\sqrt{(\\frac{\\partial{E}}{\\partial{w}})\^2+(\\frac{\\partial{E}}{\\partial{b}})\^2}}\\\\\[10pt\] =\\frac{\\sum\\limits_{i=1}\^{m}(\\hat{y_i}-y_i)}{\\sqrt{({\\sum\\limits_{i=1}\^{m}x_i(\\hat{y_i}-y_i)})\^2+(\\sum\\limits_{i=1}\^{m}(\\hat{y_i}-y_i))\^2}}\\\\\[10pt\] tanθ=∂w∂E∂b∂E=i=1∑mxi(yi\^−yi)i=1∑m(yi\^−yi)θ=arctani=1∑mxi(yi\^−yi)i=1∑m(yi\^−yi)cosθ=(∂w∂E)2+(∂b∂E)2 ∂w∂E=(i=1∑mxi(yi\^−yi))2+(i=1∑m(yi\^−yi))2 i=1∑mxi(yi\^−yi)sinθ=(∂w∂E)2+(∂b∂E)2 ∂b∂E=(i=1∑mxi(yi\^−yi))2+(i=1∑m(yi\^−yi))2 i=1∑m(yi\^−yi) 做个简化，令 η = 1 ( ∑ i = 1 m x i ( y i \^ − y i ) ) 2 + ( ∑ i = 1 m ( y i \^ − y i ) ) 2 Δ w = Δ r cos ⁡ θ = η Δ r ⋅ ∂ E ∂ w Δ b = Δ r sin ⁡ θ = η Δ r ⋅ ∂ E ∂ b \\eta= \\frac{1}{\\sqrt{({\\sum\\limits_{i=1}\^{m}x_i(\\hat{y_i}-y_i)})\^2+(\\sum\\limits_{i=1}\^{m}(\\hat{y_i}-y_i))\^2}}\\\\\[10pt\] \\Delta w=\\Delta r\\cos \\theta =\\eta\\Delta r \\cdot \\frac{\\partial{E}}{\\partial{w}}\\\\\[10pt\] \\Delta b=\\Delta r\\sin \\theta =\\eta \\Delta r \\cdot \\frac{\\partial{E}}{\\partial{b}}\\\\\[10pt\] η=(i=1∑mxi(yi\^−yi))2+(i=1∑m(yi\^−yi))2 1Δw=Δrcosθ=ηΔr⋅∂w∂EΔb=Δrsinθ=ηΔr⋅∂b∂E 参数更新后为： w t + 1 = w t − Δ w = w t − η Δ r ∂ E ∂ w b t + 1 = b t − Δ b = b t − η Δ r ∂ E ∂ b w_{t+1}=w_t-\\Delta w=w_t- \\eta \\Delta r \\frac{\\partial{E}}{\\partial{w}}\\\\\[10pt\] b_{t+1}=b_t-\\Delta b=b_t-\\eta \\Delta r \\frac{\\partial{E}}{\\partial{b}}\\\\\[10pt\] wt+1=wt−Δw=wt−ηΔr∂w∂Ebt+1=bt−Δb=bt−ηΔr∂b∂E 这就是在各种资料出现的梯度下降的公式，为了更进一步简化， 步长 η \\eta η 不用上面那么准确地求解，直接用一个很小的数值来代替，比如 0.01，步长越小，意味爬得慢，一点一点往下爬，迭代次数越多，需要很多次才走到谷底，即最后找到一组 w , b w,b w,b，使RSS达到最小。 ### 反向传播 那么到底下降多少呢？这就要定 Δ r \\Delta r Δr 了，为了简便，直接用 Δ E \\Delta E ΔE，也就是预测值与真实值之间的误差平方和。 Δ r \\Delta r Δr 与 Δ E \\Delta E ΔE 之间就像中间存在一个杠杆一样，如果误差 Δ E \\Delta E ΔE 太大，那我就调一下 Δ r \\Delta r Δr，分解对应着 Δ w \\Delta w Δw, Δ b \\Delta b Δb，让它回退一点点，就能让误差也小一点，这就是误差 `反向传播` 机制。 ### python 验证 生成一些随机数据 ```python import numpy as np import matplotlib.pyplot as plt # 生成一些随机数据 np.random.seed(0) x = 2 * np.random.rand(100, 1) y = 4 + 3 * x + np.random.randn(100, 1) # 可视化数据 plt.scatter(x, y) plt.xlabel('x') plt.ylabel('y') plt.title('Data') plt.show() ``` 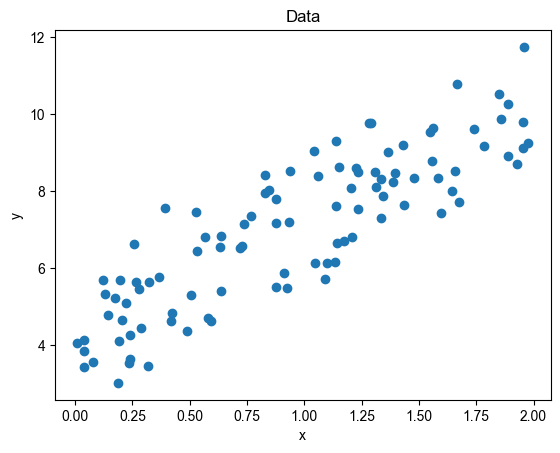 梯度下降算法实现 ```python # 初始化参数 w = 0 b = 0 m = len(x) lr = 0.01 round = 1000 #训练 for i in range(round): y_pred = w * x + b dw = (1/m) * np.sum(x * (y_pred-y)) db = (1/m) * np.sum(y_pred-y) # print(f'dw={dw},db={db}') w = w - lr * dw b = b - lr * db # 输出最终参数 print(f"w={w},b={b}") ``` 例如求得结果为：w=3.125936517774015,b=4.0446871544206235 可视化手动实现的拟合结果: ```python y_pred = w * x + b plt.scatter(x, y) plt.plot(x, y_pred, color='green') plt.xlabel('x') plt.ylabel('y') plt.title('Manual Gradient Descent Fit') plt.show() ``` 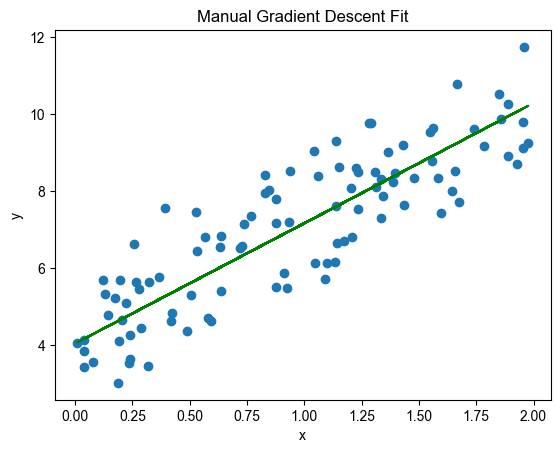 ### 均方差 MSE 有点地方要注意的是，大多数教程都是用均方差作为损失函数 M S E = 1 m R S S = 1 m ∑ i = 1 m ( y i \^ − y i ) 2 MSE=\\frac{1}{m}{RSS} =\\frac{1}{m}\\sum\\limits_{i=1}\^{m}{(\\hat{y_i}-y_i)\^2}\\\\\[10pt\] MSE=m1RSS=m1i=1∑m(yi\^−yi)2 那为了求导少带系数，再除以个2，得到 J J ( w , b ) = 1 2 M S E = 1 2 m R S S = 1 2 m ∑ i = 1 m ( y i \^ − y i ) 2 J(w,b)=\\frac{1}{2}{MSE}=\\frac{1}{2m}{RSS} =\\frac{1}{2m}\\sum\\limits_{i=1}\^{m}{(\\hat{y_i}-y_i)\^2}\\\\\[10pt\] J(w,b)=21MSE=2m1RSS=2m1i=1∑m(yi\^−yi)2 而在上面理论推导，我为了求导方便少带系数采用了 E： E = 1 2 R S S = 1 2 ∑ i = 1 m ( y i \^ − y i ) 2 E=\\frac{1}{2}{RSS}=\\frac{1}{2}\\sum\\limits_{i=1}\^{m}{(\\hat{y_i}-y_i)\^2}\\\\\[10pt\] E=21RSS=21i=1∑m(yi\^−yi)2 J 比 E 多除了个 m，即： J = 1 2 m R S S = 1 m E J=\\frac{1}{2m}{RSS}=\\frac{1}{m}{E} J=2m1RSS=m1E 影响梯度偏导也多除一个 m，即： ∇ J ⃗ = \[ ∂ J ∂ w ∂ J ∂ b \] \[ 1 m ∑ i = 1 m x i ( y i \^ − y i ) 1 m ∑ i = 1 m ( y i \^ − y i ) \] \\nabla \\vec{J}=\\begin{bmatrix} \\frac{\\partial{J}}{\\partial{w}}\\\\\[10pt\] \\frac{\\partial{J}}{\\partial{b}} \\end{bmatrix}\\begin{bmatrix} \\frac{1}{m}\\sum\\limits_{i=1}\^{m}x_i(\\hat{y_i}-y_i)\\\\\[10pt\] \\frac{1}{m}\\sum\\limits_{i=1}\^{m}(\\hat{y_i}-y_i) \\end{bmatrix} ∇J = ∂w∂J∂b∂J m1i=1∑mxi(yi\^−yi)m1i=1∑m(yi\^−yi) 这样会让反向传播中的 Δ E \\Delta E ΔE 小一点，相应地 Δ w , Δ b \\Delta w,\\Delta b Δw,Δb 也会变化小点，我程序上也用的是这个 ```python dw = (1/m) * np.sum(x * (y_pred-y)) db = (1/m) * np.sum(y_pred-y) ``` 从训练结果上来看，这个常量不会对最终结果有什么影响，但会影响步长，从而影响收敛速度。 有一点要注意，m 必须大于1，这里所讲的 m 仅仅是一个数值，并不代表样本总数，也就是 `(1/m)` 这个系数要小于1，不然结果离谱得很，会发散数值溢出，而当 m \>1，即 `(1/m)` 这个系数小于1 时，结果收敛，它的作用也有可能就是想让计算机在计算时避免大数值的溢出。 造成与理论差异关键就在于实用时用估算值替代，比如 η \\eta η 直接是用 0.01 估算， Δ r \\Delta r Δr 也直接用 Δ E \\Delta E ΔE 来代替，这些都可能影响到训练时的步长。 下面是程序实验计算的结果: 1. `m=1` 时，结果已经发散，求不出 w 与 b，即 ```bash # dw = np.sum(x * (y_pred-y)) # db = np.sum(y_pred-y) dw=-850.1683501683501,db=3.552713678800501e-15 dw=6377.693886111394,db=-4.263256414560601e-14 dw=-47843.44100422958,db=4.547473508864641e-13 dw=358906.352045197,db=-1.8189894035458565e-12 dw=-2692401.859786865,db=1.2732925824820995e-11 ... dw=-5.4253529775673765e+305,db=7.918067634262499e+288 dw=4.069928092262665e+306,db=-7.308985508549999e+289 dw=-3.053131242276504e+307,db=9.745314011399999e+290 dw=inf,db=-1.559250241824e+290 dw=-inf,db=nan ``` 1. `m=2`时，得到结果与最小二乘法算到的是一样大小： ```bash # dw = 1/2 * np.sum(x * (y_pred-y)) # db = 1/2 * np.sum(y_pred-y) dw=-381.677900861596,db=-351.4548690576116 dw=18.57224973839901,db=4.727525676626343 dw=4.946675978330024,db=-6.4170824238898465 dw=4.946818532305948,db=-5.547299140563914 dw=4.535645479339176,db=-5.112474897542561 dw=4.171064141390431,db=-4.700662689615653 ... dw=1.2484696436387832e-14,db=-2.4868995751603507e-14 dw=1.2484696436387832e-14,db=-2.4868995751603507e-14 dw=1.2484696436387832e-14,db=-2.4868995751603507e-14 w=2.9684675107010214,b=4.222151077447227 ``` 1. `m=len(x)=100` 时，也就是与样本数量一致时： ```bash # dw = 1/m * np.sum(x * (y_pred-y)) # db = 1/m * np.sum(y_pred-y) dw=-7.633558017231921,db=-7.029097381152232 dw=-7.47345795699192,db=-6.886624423258533 dw=-7.316668902546804,db=-6.747090081387518 dw=-7.163122453666059,db=-6.6104336609161045 dw=-7.012751623042291,db=-6.4765957209516 dw=-6.865490807105078,db=-6.345518048433969 dw=-6.721275757437722,db=-6.217143632773047 dw=-6.580043552784417,db=-6.091416641009688 ... dw=0.025467711868425648,db=-0.028701534563458184 dw=0.025426721224795897,db=-0.028655338763381374 dw=0.02538579655360806,db=-0.0286092173188295 w=3.125936517774015,b=4.0446871544206235 ``` 当 `m=2*len(x) =200` 时， ```bash # dw = 1/(2*m) * np.sum(x * (y_pred-y)) # db = 1/(2*m) * np.sum(y_pred-y) dw=-3.8167790086159603,db=-3.514548690576116 dw=-3.776753993555959,db=-3.4789304511026917 dw=-3.7371428542203198,db=-3.443679538632103 dw=-3.6979413155946346,db=-3.4087921597504054 dw=-3.659145146818342,db=-3.3742645602227346 dw=-3.620750160728698,db=-3.340093024588643 dw=-3.582752213409447,db=-3.3062738757616335 ... dw=0.028309798773081957,db=-0.032154331529856306 dw=0.028288197439600916,db=-0.03212740685678457 dw=0.028266601289693175,db=-0.03210051467730426 w=3.320819548442338,b=3.8248240221727645 ```