文章目录
- [week54 MAGNA](#week54 MAGNA)
- 摘要
- Abstract
- 一、文献阅读
-
- [1. 题目](#1. 题目)
- [2. Abstract](#2. Abstract)
- [3. 文献解读](#3. 文献解读)
-
- [3.1 Introduce](#3.1 Introduce)
- [3.2 创新点](#3.2 创新点)
- [4. MAGNA](#4. MAGNA)
-
- [4.1 基础](#4.1 基础)
- [4.2 多跳注意力扩散机制](#4.2 多跳注意力扩散机制)
- [4.3 网络架构](#4.3 网络架构)
- [4.4 图注意力扩散机制的分析](#4.4 图注意力扩散机制的分析)
- [5. 实验分析](#5. 实验分析)
-
- [5.1 节点分类](#5.1 节点分类)
- [5.2 知识图谱](#5.2 知识图谱)
- 6.结论
- 二、若依系统
-
- [1. 权限管理](#1. 权限管理)
- [2. 数据字典](#2. 数据字典)
- [3. 其他功能](#3. 其他功能)
-
- [3.1 参数设置](#3.1 参数设置)
- [3.2 通知公告(半成品)](#3.2 通知公告(半成品))
- [3.3 日志管理](#3.3 日志管理)
- 三、大数据相关
week54 MAGNA
摘要
本周阅读了题为Multi-hop Attention Graph Neural Network的论文。该文提出MAGNA,整合多跳上下文信息到GNN每层注意计算中,增强网络注意力分布,扩大每层"接受场"。MAGNA采用注意力扩散先验,有效解释非连接节点间路径。理论和实验证明,MAGNA捕获大规模结构信息,具低通效应,去噪高频信息。在节点分类和知识图谱基准上,MAGNA达最先进结果,相对误差降5.7%。在大规模图数据集上表现强劲,并在知识图谱完成上推进WN18RR和FB15k-237的四个性能指标。
Abstract
This week's weekly newspaper decodes the paper entitled Multi-hop Attention Graph Neural Network. This paper introduces MAGNA, which integrates multi-hop contextual information into the attention computation of each layer in GNNs, enhancing the distribution of network attention and expanding the "receptive field" of each layer. MAGNA employs an attention diffusion prior to effectively interpret paths between non-connected nodes. Both theoretically and experimentally, it is proven that MAGNA captures large-scale structural information, exhibits a low-pass effect, and removes noisy high-frequency information. On node classification and knowledge graph benchmarks, MAGNA achieves state-of-the-art results with a 5.7% relative error reduction compared to previous state-of-the-art techniques on Cora, Citeseer, and Pubmed. MAGNA also demonstrates robust performance on large-scale graph datasets and advances the four performance metrics of WN18RR and FB15k-237 in knowledge graph completion.
一、文献阅读
1. 题目
标题:Multi-hop Attention Graph Neural Network
作者:Guangtao Wang, Rex Ying, Jing Huang, Jure Leskovec
发布:IJCAI2021 A会
链接:https://arxiv.org/abs/2009.14332v5
代码链接:https://github.com/xjtuwgt/gnn-magna
2. Abstract
该文提出了多跳注意图神经网络(Multi-hop Attention Graph Neural Network, MAGNA),这是一种将多跳上下文信息整合到GNN注意计算的每一层的原则方法。MAGNA在整个网络中确定注意力的分布,这增加了GNN每一层的"接受场"(receptive field)。与以前的方法不同,MAGNA使用了注意力值的扩散先验方法,以有效地解释一对非连接节点之间的所有路径。从理论和实验上证明,MAGNA在每一层中捕获大规模的结构信息,并具有低通效应,从图中消除噪声高频信息。节点分类和知识图谱完成基准的实验结果表明,MAGNA达到了最先进的结果:与Cora、Citeseer和Pubmed上的先前最先进的技术相比,MAGNA达到了5.7%的相对误差降低。MAGNA还在大规模开放图基准数据集上获得了强大的性能。最后,在知识图谱完成方面,MAGNA在四个不同的性能指标上推进了WN18RR和FB15k-237的最先进技术。
3. 文献解读
3.1 Introduce
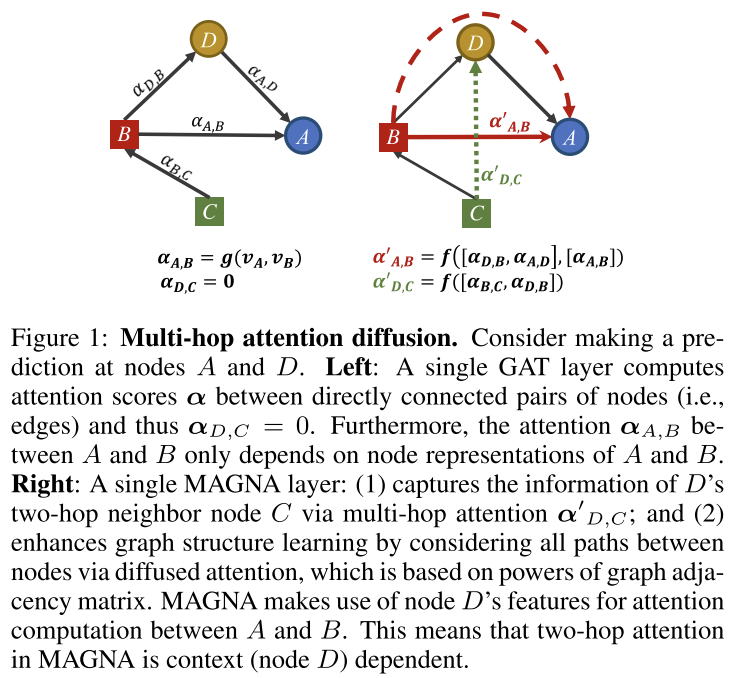
该文提出了一种有效的多跳自注意机制------多跳注意图神经网络(MAGNA)。MAGNA使用了一种新颖的图注意力扩散层(图1),首先计算边缘上的注意力权重(用实线箭头表示),然后通过使用边缘上的注意力权重的注意力扩散过程,计算不相连的节点对之间的自注意力权重(虚线箭头)。
在标准数据集上进行了半监督节点分类和知识图补全的实验。实验表明,MAGNA达到了最先进的结果:MAGNA在Cora、Citeseer和Pubmed上实现了5.7%的相对误差降低。MAGNA在大规模Open Graph基准数据集上也获得了更好的性能。在知识图谱完成方面,麦格纳在WN18RR和FB15k-237的四个指标上都取得了最先进的进步,其中Hit指标的最大增幅为7.1%,达到1。
该文实验表明,3层和每层6跳宽注意力的MAGNA显著优于具有18层的GAT,即使这两种架构具有相同的接受场。此外,消融研究揭示了MAGNA基本成分的协同作用,包括层归一化和多跳扩散注意。进一步观察到,与GAT相比,MAGNA学习到的注意值具有更高的多样性,表明它能够更好地关注重要节点。
3.2 创新点
模型有两个主要优点:
- MAGNA捕获了不直接连接但可能有多个跳的节点之间的远程交互。因此,该模型支持从多个跳之外的重要节点有效地进行远程消息传递。
- MAGNA的注意力计算是上下文相关的。相较于GAT,对于所选的多跳邻域内的任何一对节点,MAGNA通过将连接这两个节点的所有可能路径(长度≥1)的注意力得分聚合在一起来计算注意力。
- 进一步应用谱图分析表明,MAGNA强调大规模的图结构和降低图中的高频噪声。
4. MAGNA
4.1 基础
设 G = ( V , E ) \mathcal G = (\mathcal V, \mathcal E) G=(V,E)为给定图,其中 V \mathcal V V为 N n N_n Nn个节点的集合, E ⊆ V × V \mathcal E\subseteq \mathcal V\times \mathcal V E⊆V×V为连接 V \mathcal V V中M对节点的 N e N_e Ne个边的集合。每个节点 v ∈ V v\in \mathcal V v∈V和每个边 e ∈ E e\in \mathcal E e∈E与其类型映射函数 ϕ : V → T \phi:\mathcal V\rightarrow \mathcal T ϕ:V→T和 ψ E → R \psi \mathcal E\rightarrow \mathcal R ψE→R。相关联,其中 T \mathcal T T和 R \mathcal R R为节点类型(标签)和边/关系类型的集合。该框架支持在具有多个 R \mathcal R R元素的异构图上学习。
一般的图神经网络(GNN)方法学习将节点和/或边类型映射到连续向量空间的嵌入。设 X ∈ R N n × d n , X\in \mathbb R^{N_n\times d_n}, X∈RNn×dn, R ∈ R N r × d r R\in \mathbb R^{N_r\times d_r} R∈RNr×dr为节点嵌入和边/关系类型嵌入,其中 N n = ∣ V ∣ , N r = ∣ R ∣ N_n=|\mathcal V|, N_r = |\mathcal R| Nn=∣V∣,Nr=∣R∣, d n d_n dn和 d r d_r dr表示节点和边/关系类型的嵌入维数,每一行 x i = X [ i : ] x_i = X[i:] xi=X[i:]表示节点 v i ( 1 ≤ i ≤ N n ) v_i(1≤i≤N_n) vi(1≤i≤Nn)的嵌入, r j = R [ j : ] r_j = R[j:] rj=R[j:]表示关系 r j ( 1 ≤ j ≤ N r ) r_j(1≤j≤N_r) rj(1≤j≤Nr)的嵌入。MAGNA建立在gnn的基础上,同时汇集了图注意和扩散技术的优点。
4.2 多跳注意力扩散机制
首先引入注意力扩散来直接计算多跳注意力,这对每一层的注意力分数起作用。注意扩散算子的输入是一组三元组 ( v i , r k , v j ) (v_i, r_k, v_j) (vi,rk,vj),其中 v i , v j v_i, v_j vi,vj是节点, r k r_k rk是边缘类型。MAGNA首先计算所有边缘的注意力得分。然后,注意力扩散模块根据边缘注意力得分,通过扩散过程计算不直接由边缘连接的节点对之间的注意力值。然后,注意力扩散模块可以用作MAGNA架构中的一个组件
边缘关注计算:
在每一层l,为每个三元组 ( v i , r k , v j ) (v_i, r_k, v_j) (vi,rk,vj)计算一个向量消息。为了计算 v j v_j vj在第1层的表示,从事件到 v j v_j vj的三元组的所有消息聚合为单个消息,然后使用该消息更新 v j l + 1 v^{l+1}_j vjl+1。
在第一阶段,计算一条边 ( v i , r k , v j ) (v_i, r_k, v_j) (vi,rk,vj)的注意力分数s,方法如下:
s i , k , j ( l ) = δ ( v a ( l ) tanh ( W h ( l ) h i ( l ) ∣ ∣ W t ( l ) r k ∣ ∣ ) s^{(l)}_{i,k,j}=\delta(v^{(l)}_a\tanh (W_h^{(l)}h^{(l)}_i||W^{(l)}_tr_k||) si,k,j(l)=δ(va(l)tanh(Wh(l)hi(l)∣∣Wt(l)rk∣∣)
在图G的每条边上应用Eq. 1,得到一个注意力得分矩阵S(l)。
S ( l ) = { { s i , k , j ( l ) , if ( v i , r k , v j ) appears in G − inf , otherwise S^{(l)}=\begin{cases} \{s^{(l)}_{i,k,j},\quad \text{if}\ (v_i,r_k,v_j)\ \text{appears in}\mathcal G \\ -\inf, \text{otherwise} \end{cases} S(l)={{si,k,j(l),if (vi,rk,vj) appears inG−inf,otherwise
随后,通过在分数矩阵S(l)上执行逐行softmax来获得注意力矩阵 S ( l ) : A ( l ) = s o f t m a x ( S ( l ) ) S^{(l)}: A^{(l)} = softmax(S^{(l)}) S(l):A(l)=softmax(S(l))。 A i j ( l ) A^{(l)}_{ij} Aij(l)表示从节点j向节点i聚合消息时在第l层的关注值。
多跳邻接节点的注意力扩散机制:
在第二阶段,进一步在网络中不直接连接的节点之间启用注意。通过以下注意扩散程序来实现这一点。该过程基于单跳注意矩阵A的幂,通过图扩散计算多跳邻居的注意分数:
KaTeX parse error: Got function '\inf' with no arguments as superscript at position 19: ...athcal A= \sum^\̲i̲n̲f̲_{i=0}\theta_i\...
注意矩阵的幂,Ai将从节点h到节点t关系路径的数量最长长度增长至i,增加了注意力的接受域(图1)。重要的是,该机制允许两个节点之间的注意力不仅依赖于它们之前的层表示,而且考虑到节点之间的路径,有效地在不直接连接的节点之间创建注意力捷径(图1)。根据θ和路径长度,每个路径的注意力权重也不同。
在实现中,利用几何分布 θ i = α ( 1 − α ) i θ_i = α(1−α)^i θi=α(1−α)i,其中 α ∈ ( 0 , 1 ) α∈(0,1) α∈(0,1)。该选择基于消息聚合中距离较远的节点权重较小的归纳偏差,并且与目标节点的关系路径长度不同的节点以独立的方式顺序加权。此外,请注意,若定义 θ 0 = α ∈ ( 0 , 1 ] , A 0 = I θ_0 = α\in (0,1], A^0 = I θ0=α∈(0,1],A0=I,则Eq. 3给出了具有注意力矩阵A和传送概率α的图上的个性化页面排名(PPR)过程。因此,分散的注意力权重Aij可以看作是节点j对节点i的影响。
可将Aij看作是节点j到节点i的关注值,因为 ∑ j = 1 N n A i j = 1 \sum^{Nn}{j=1} \mathcal A{ij} = 1 ∑j=1NnAij=1,将基于图注意力扩散的特征聚合定义为
AttDiff ( G , H ( l ) , θ ) = A H ( l ) \text{AttDiff}(\mathcal G,H^{(l)},\theta)=\mathcal AH^{(l)} AttDiff(G,H(l),θ)=AH(l)
由于在Eq. 3中定义的扩散过程,MAGNA使用了相同数量的参数。这确保了运行时效率和模型泛化。
注意力扩散机制的计算拟合
对于大型图,由于计算注意力矩阵的幂,使用Eq. 3计算精确的注意力扩散矩阵A可能会非常昂贵。为了解决这个瓶颈,进行如下操作:设 H ( l ) H^{(l)} H(l)为第l层的输入实体嵌入( H ( 0 ) = X H^{(0)} = X H(0)=X), θ i = α ( 1 − α ) i θ_i = α(1−α)^i θi=α(1−α)i。由于MAGNA只需要通过 A H ( l ) \mathcal AH^{(l)} AH(l)进行聚合,可以通过定义一个收敛于AH(l)的真值(命题1)为 K → ∞ K→∞ K→∞的序列 Z ( K ) Z^{(K)} Z(K)来近似 A H ( l ) \mathcal AH{(l)} AH(l):
Z ( 0 ) = H ( l ) , Z ( k + 1 ) = ( 1 − α ) A Z ( k ) + α Z ( 0 ) Propostion 1 lim K → + inf Z ( K ) = A H ( l ) Z^{(0)}=H^{(l)},Z^{(k+1)}=(1-\alpha)AZ^{(k)}+\alpha Z^{(0)}\\ \text{Propostion\ 1}\ \lim_{K\rightarrow +\inf}Z^{(K)}=\mathcal AH^{(l)} Z(0)=H(l),Z(k+1)=(1−α)AZ(k)+αZ(0)Propostion 1 K→+inflimZ(K)=AH(l)
使用上述近似,带扩散的注意力计算的复杂度仍然为 O ( ∣ E ∣ ) O(|E|) O(∣E∣),并且有一个常数因子对应于跳数K。在实践中,发现选择K的值使3≤K≤10可以获得良好的模型性能。许多真实世界的图都表现出小世界性质,在这种情况下,更小的k值就足够了。对于直径较大的图,选择较大的K,并降低α值。
4.3 网络架构
图2提供了可以多次堆叠的MAGNA块的体系结构概述。

多头图注意力扩散层
使用多头注意力来允许模型在不同视点上共同关注来自不同表示子空间的信息。在Eq. 6中,每个头i的注意力扩散分别用Eq. 4计算,汇总为:
H ^ ( l ) = MultiHead ( G , H ^ ( l ) ) = ( ∣ ∣ i = 1 M head i ) W o head i = AttDiff ( G , H ^ ( l ) , Θ i ) , H ^ ( l ) = LN ( H ( l ) ) \hat H^{(l)}=\text{MultiHead}(\mathcal G,\hat H^{(l)})=(||^M_{i=1}\text{head}_i)W_o\\ \text{head}_i=\text{AttDiff}(\mathcal G,\hat H^{(l)},\Theta_i),\hat H^{(l)}=\text{LN}(H^{(l)}) H^(l)=MultiHead(G,H^(l))=(∣∣i=1Mheadi)Woheadi=AttDiff(G,H^(l),Θi),H^(l)=LN(H(l))
由于在Eq. 5中以递归方式计算注意力扩散,因此添加了层归一化,这有助于稳定递归计算过程
深度聚合
MAGNA块包含一个完全连接的前馈子层,该子层由两层前馈网络组成。还在两个子层中添加了层归一化和残差连接,从而允许对每个块进行更具表现力的聚合步骤
H ^ ( l + 1 ) = H ^ ( l ) + H ( l ) H ( l + 1 ) = W 2 ( l ) ReLU ( W 1 ( l ) LN ( H ^ ( l + 1 ) ) ) + H ^ ( l + 1 ) \hat H^{(l+1)}=\hat H^{(l)}+H^{(l)}\\ H^{(l+1)}=W_2^{(l)}\text{ReLU}(W^{(l)}_1\text{LN}(\hat H^{(l+1)}))+\hat H^{(l+1)} H^(l+1)=H^(l)+H(l)H(l+1)=W2(l)ReLU(W1(l)LN(H^(l+1)))+H^(l+1)
基于GAT的扩展
MAGNA通过扩散过程扩展了GAT。GAT中的特征聚合为 H ( 1 ) = σ ( A H ( l ) W ( l ) ) H^{(1)} = σ(\mathcal AH^{(l)}W^{(l)}) H(1)=σ(AH(l)W(l)),其中σ表示激活函数。可以将GAT层分为以下两个部分:
H ( l + 1 ) = σ ⏟ ( 2 ) ( A H ( l ) W ( l ) ) ⏟ ( 1 ) H^{(l+1)}=\underbrace {\sigma}{(2)}\underbrace {(AH^{(l)}W^{(l)})}{(1)} H(l+1)=(2) σ(1) (AH(l)W(l))
4.4 图注意力扩散机制的分析
图注意扩散的谱性质
将gat的注意力矩阵A和MAGNA的注意力矩阵A视为加权邻接矩阵,并应用图傅立叶变换和频谱分析来显示MAGNA作为图低通滤波器的效果,能够更有效地捕获图中的大规模结构。根据公式3, A \mathcal A A或A的每一行之和为1。因此,对于 A \mathcal A A和A,归一化图拉普拉斯算子分别为 L ^ s y m = I − A , L s y m = I − A \hat L_{sym} = I - \mathcal A,L_{sym} = I - A L^sym=I−A,Lsym=I−A。可以得到以下命题:
命题2 :令 λ ^ i g a n d λ i g \hat \lambda^g_i\ and\ \lambda^g_i λ^ig and λig为矩阵 L ^ s y m a n d L s y m \hat L_{sym}\ and\ L_{sym} L^sym and Lsym的第i个特征值
λ ^ i g λ i g = 1 − a 1 − ( 1 − α ) ( 1 − λ i g ) λ i g = 1 α 1 − α + λ i g \frac{\hat \lambda^g_i}{\lambda^g_i}=\frac{1-\frac a{1-(1-\alpha)(1-\lambda^g_i)}}{\lambda^g_i}=\frac 1{\frac{\alpha}{1-\alpha}+\lambda^g_i} λigλ^ig=λig1−1−(1−α)(1−λig)a=1−αα+λig1
由式9可知,当 λ i g λ^g_i λig较小时,使得 α 1 − α + λ i g < 1 \frac{α} {1 - α} +λ^g_i < 1 1−αα+λig<1时, λ ^ i g > λ i g \hat λ^g_i > λ^g_i λ^ig>λig,而当 λ i g λ^g_i λig较大时, λ ^ i g < λ i g \hat λ^g_i < λ^g_i λ^ig<λig。这种关系表明, A \mathcal A A的使用增加了较小的特征值,减少了较大的特征值4。低通效应随α的减小而增大。
低频信号的特征值描述了图中的大规模结构,并且在图任务中被证明是至关重要的。当 λ i g ∈ [ 0 , 2 ] λ^g_i\in [0,2] λig∈[0,2]且 α 1 − α > 0 \frac{\alpha} {1−α} > 0 1−αα>0时,Eq. 9中的倒数格式将把较低特征值的比例放大为所有特征值的总和。相反,噪声对应的高特征值被抑制。
独特PageRank满足图注意力扩散
可以将注意力矩阵A看作是图G上的随机游走矩阵,因为 ∑ j = 1 N n A i , j = 1 a n d A i , j > 0 \sum^{N_n}{j=1} A{i,j} =1\ and\ A_{i,j} > 0 ∑j=1NnAi,j=1 and Ai,j>0。如果对具有转移矩阵A的G执行参数 α ∈ ( 0 , 1 ) α∈(0,1) α∈(0,1)的独特PageRank (PPR),则PPR的完全定义为:
A p p r = α ( I − ( 1 − α ) A ) − 1 A_{ppr}=\alpha(I-(1-\alpha)A)^{-1} Appr=α(I−(1−α)A)−1
利用矩阵逆的幂级数展开式,得到
KaTeX parse error: Got function '\inf' with no arguments as superscript at position 21: ...pr}=\alpha\sum^\̲i̲n̲f̲_{i=1}(1-\alpha...
有如下命题
Proposition 3 : \text{Proposition}\ 3: Proposition 3:图注意力扩散机制在 G \mathcal G G上定义了一个由 α ∈ ( 0 , 1 ) \alpha\in(0,1) α∈(0,1)确定的PPR, G \mathcal G G转移矩阵为 A A A
MAGNA中的参数α相当于PPR的传送概率。PPR提供了加权图中节点之间的良好相关性分数(来自注意力矩阵a的权重)。总之,MAGNA将PPR置于节点对注意力分数之上:节点i和j之间的分散注意力取决于节点i和j之间所有路径边缘上的注意力分数。
5. 实验分析
5.1 节点分类


数据集
使用四个基准数据集进行节点分类:(1)标准引文网络基准Cora、Citeseer和Pubmed ;Kipf;(2)基于开放图基准的170k个节点和1.2m条边的基准数据集ogbn-arxiv。遵循所有数据集的标准数据分割。关于这些数据集的进一步信息总结在附录中。
基线
使用四个基准数据集进行节点分类:(1)标准引文网络基准Cora、Citeseer和Pubmed ;(2)基于开放图基准的170k个节点和1.2m条边的基准数据集ogbn-arxiv。遵循所有数据集的标准数据分割。关于这些数据集的进一步信息总结在附录中。我们比较了一套全面的最先进的GNN方法,包括:gcn,基于Chebyshev滤波器的gcn,DualGCN, JKNet,LGCN ,扩散- gcn (Diff-GCN), APPNP, Graph U-Nets (g-U-Nets)和GAT
实验设置
对于Cora, Citeseer和Pubmed数据集,使用6个MAGNA块,隐藏维度512和8个注意头。对于大规模ogbn-arxiv数据集,使用2个隐藏维度为128的MAGNA块和8个注意头。
结果
MAGNA在所有数据集上都取得了最好的成绩(表1和表2),优于多跳基线,如Diffusion GCN、APPNP和JKNet。基准性能和它们的嵌入维度来自先前的论文。进一步表明,大的512维嵌入只有利于表达性的MAGNA,而GAT和扩散GCN性能下降。
消融实验
报告了(表1)从每个MAGNA层中去除MAGNA各组成部分(层归一化、注意扩散和前馈层)后的模型性能。注意,该模型相当于没有这三个组件的GAT。我们观察到扩散和层归一化在提高所有数据集的节点分类性能方面起着至关重要的作用。由于MAGNA以递归方式计算注意力扩散,因此层归一化对于确保训练稳定性至关重要。同时,与GAT(见表1倒数第二行)相比,注意扩散允许每层中的多跳注意,从而有利于节点分类
5.2 知识图谱
数据集
我们在标准基准知识图上评估MAGNA: WN18RR [Dettmers等,2018]和FB15K-237 [Toutanova和Chen, 2015]。这些kg的统计数据见附录。
基线
我们将MAGNA与最先进的基线进行了比较,包括(1)基于翻译距离的模型:TransE [Bordes et al., 2013]及其最新扩展RotatE [Sun et al., 2019]、OTE [Tang et al., 2020]和ROTH [Chami et al., 2020];(2)基于语义匹配的模型:ComplEx [Trouillon et al., 2016], QuatE [Zhang et al., 2019], CoKE [Wang et al., 2019b], ConvE [Dettmers et al., 2018], DistMult [Yang et al., 2015], TuckER [Balazevic et al., 2019]和AutoSF [Zhang et al., 2020b];(3)基于gnn的模型:R-GCN [Schlichtkrull等人,2018],SACN [Shang等人,2019]和A2N [Bansal等人,2019]。
实验设置
我们使用多层MAGNA作为FB15k-237和WN18RR的编码器。我们随机初始化实体嵌入和关系嵌入作为编码器的输入,并将初始化的实体/关系向量的维数设置为DistMult中使用的100 [Yang et al., 2015]。我们在训练过程中通过随机搜索选择其他MAGNA模型的参数,包括层数、隐藏维数、头数、top-k、学习率、跳数、传送概率α和dropout比率(参见附录中这些参数的设置)。
训练过程
我们使用了以前的KG嵌入模型中使用的标准训练程序Balazevic等人,2019;Dettmers等人,2018。我们遵循一个编码器-解码器框架:编码器应用提出的MAGNA模型来计算实体嵌入。解码器在给定嵌入的情况下进行链路预测。为了展示MAGNA的强大功能,我们使用了一个简单的解码器DistMult [Yang et al., 2015]。
评估标准
我们在基准测试中使用标准分割,并在给定头(尾)实体和关系类型的情况下使用预测尾(头)实体的标准测试程序。我们完全遵循之前所有作品使用的评估,即平均倒数秩(MRR),平均秩(MR)和K的命中率(H@K)。关于这个标准设置的详细描述,请参见附录。
实验结果
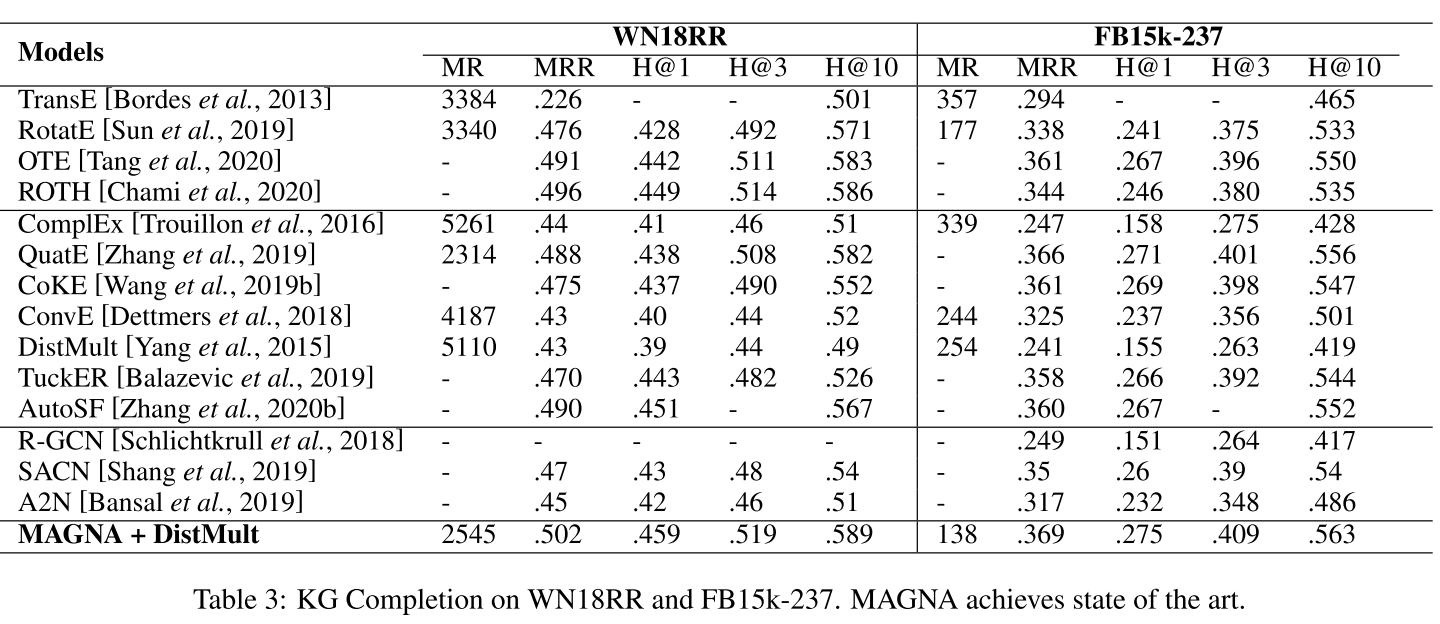
MAGNA在所有四个指标上都实现了最先进的知识图谱完成(表3)。与最新的浅嵌入方法(QuatE)和深嵌入方法(SACN)相比,MAGNA都具有优势。请注意,使用相同的解码器(DistMult), MAGNA使用自己的嵌入比使用相应的DistMult嵌入实现了巨大的改进。
6.结论
本文提出了多跳注意图神经网络(Multi-hop Attention Graph Neural Network, MAGNA),通过注意扩散、层归一化和深度聚合,将图注意和扩散技术的优点融合在一个单层中。MAGNA支持在单层图中任意对节点之间的上下文依赖的注意力,增强大规模的结构信息,并学习更多信息的注意力分布。MAGNA在节点分类和知识图完成的标准任务上改进了所有最新的方法。
二、若依系统
系统管理、系统监控、系统工具三个模块
系统管理:
- 权限管理
- 数据字典
- etc(通知公告、日志管理)
1. 权限管理
前置思想:RBAC(roll based access control)通过角色 来分配和管理用户 的菜单权限
给用户 定义角色 ,给角色 分配权限
通过给单个用户分配多个角色实现权限的扩展,单个角色下辖多个用户(多对多,需要中间表)
角色与权限也是多对多关系,需要中间表

表关系如下

创建用户 小智并关联科研人员角色 ,权限仅限课程管理和统计分析菜单访问
-
创建菜单
- 菜单类型:
- 目录菜单,点击后展开目录
- 页面菜单,点击后展开页面
- 按钮菜单,点击按钮弹出对话框
- 在系统管理的菜单管理界面点击新建
- 创建统计分析菜单,类型为目录菜单,填充必要信息
- 重新进入后,统计分析界面为空
- 创建客户统计菜单,类型为页面菜单,设置在统计分析下(默认为主类目)
- 菜单类型:
-
创建角色,并分配权限
- 在角色管理界面点击新建
- 创建科研人员角色,角色顺序3,授予课程管理和统计分析权限
-
创建用户,并关联角色
- 在用户管理界面点击新建
- 创建小智角色,填充必要信息,在角色部分添加科研人员
-
重新使用小智账号登录,菜单目录如下

2. 数据字典
若依系统内置的数据字典,用于维护系统中常见的静态数据,便于维护
功能:字典类型管理,字典数据管理
表关系说明:
- sys_dict_type,字典类型表
- sys_dict_data,字典数据表
通过key查找value,这样可以将长数据存储为短数据,从而减少数据的存储空间
将课程管理的学科字段 改为数据字典维护
- 添加数据字典类型和数据
- 点击目录菜单字典管理
- 添加字典类型,编写完成后点击进入
- 点击新增,编写字典数据
- 修改代码生成信息
- 点击目录菜单代码
- 修改课程管理,将学科字段修改为下拉框关联新建的学科(数据字典)
- 点击提交
- 下载代码,导入
- 下载代码
- 只需修改前端页面,后端在提交后已经完成修改,ruoyi/vue/view
- 先将对应的course部分删除,然后将新生成的部分插入即可
- 测试功能
3. 其他功能
3.1 参数设置
对系统中参数进行动态维护。在网页中就能完成修改,不需要重启或者操作文件等
- 打开参数设置界面
- 修改验证码开关,将参数键值修改为false
- 退出当前用户,验证功能
关于用户注册
- 该参数的默认状态为false
- 首先在参数设置界面完成操作,将状态修改为true
- 有两个方法进行注册
- 将链接后缀修改为register
- 在登录界面点击注册按钮跳转至注册界面
- 需要将视图部分views的login.vue的第97行代码const register = ref(false);
- 将该部分设置为true,保存后重新加载注册界面
3.2 通知公告(半成品)
促进组织内部信息传递
- 进入通知公告界面,点击新增
- 填充后点击确定
但该功能仅提供了通知公告的录入并没有提供推送
3.3 日志管理
可以查看登录日志(查看用户的登录操作)、操作日志(用户在什么界面执行了什么操作,操作是否成功,耗时、请求参数)
系统日志随着系统运行会不断累积,这使得数据库背负不必要的运载压力。对于这种情况,可以设置定时清空日志,或者将日志内容导出后另行保存
三、大数据相关
注:以下均基于arm架构的mac系统
1. vmware配置
搜索:"vmware for mac",购买正版并下载,或通过其他渠道下载均可
2. 下载镜像并安装虚拟机
bug记录1
此处选用ubuntu的20以及24,分别出现无法加载安装程序、x86无法适配arm系统。
- 在虚拟机的设置界面,选中CDC,配置镜像地址。
- 将虚拟机重启后会进入安装界面
- bug:并未进入,重启后进入boot系统
- 在boot中,手动将CDC加载的优先级调整至最高,应用后重启,仍然无法解决
前者原因难以判断,但后者是由于下载了基于windows系统的ubuntu导致的,在下载中应注意标记ubuntu-ports等与mac系统相关关键词
bug记录2
此处选用centos9,正常进入安装程序,但选择完语言后进度卡住,选择后无限返回至选择语言界面。预计更换centos7继续安装
bug记录3
https://cloud.tencent.com/developer/article/2416622
该文直接分区,然后加载ubuntu,还是找iso文件吧............
在分区后合并分区,搜索磁盘工具,点击分区,选中想要删除的分区并点击"---",最后应用,即可合并
安装记录
- 下载镜像
- https://ubuntu.com/download/server/arm
- 以上为适配于arm系统的ubuntu,该链接为官方服务器端下载链接
- Tip:并未找到国内镜像源,部分国内镜像源主要包含基于arm的插件工具,不包含安装用iso。下载过程可能较长
- 基于vmware安装虚拟机
3. 虚拟机配置
该部分内容不分先后,没有遇到的问题可以直接跳过
- 安装桌面
- 上述服务器端安装完成后默认为命令行,如需安装桌面版,参照该链接https://blog.csdn.net/qq_24950043/article/details/125774990
- 请注意,最好先更换至国内源再安装桌面版
- 过程非常长漫长

-
点击setting,搜索lan,点击语言,选中下载/删除语言,选中简体中文并下载
-
过程中发现部分磁盘空间爆了,就剩KB级别的空间了,故扩容
-
扩容前先清理盘空间
linux系统垃圾清理 # 清理旧版本的软件缓存,删除你已经卸载掉的软件包 sudo apt-get autoclean # 清理所有软件缓存,电脑上存储的安装包全部卸载 sudo apt-get clean # 删除系统不再使用的孤立软件 sudo apt-get autoremove -
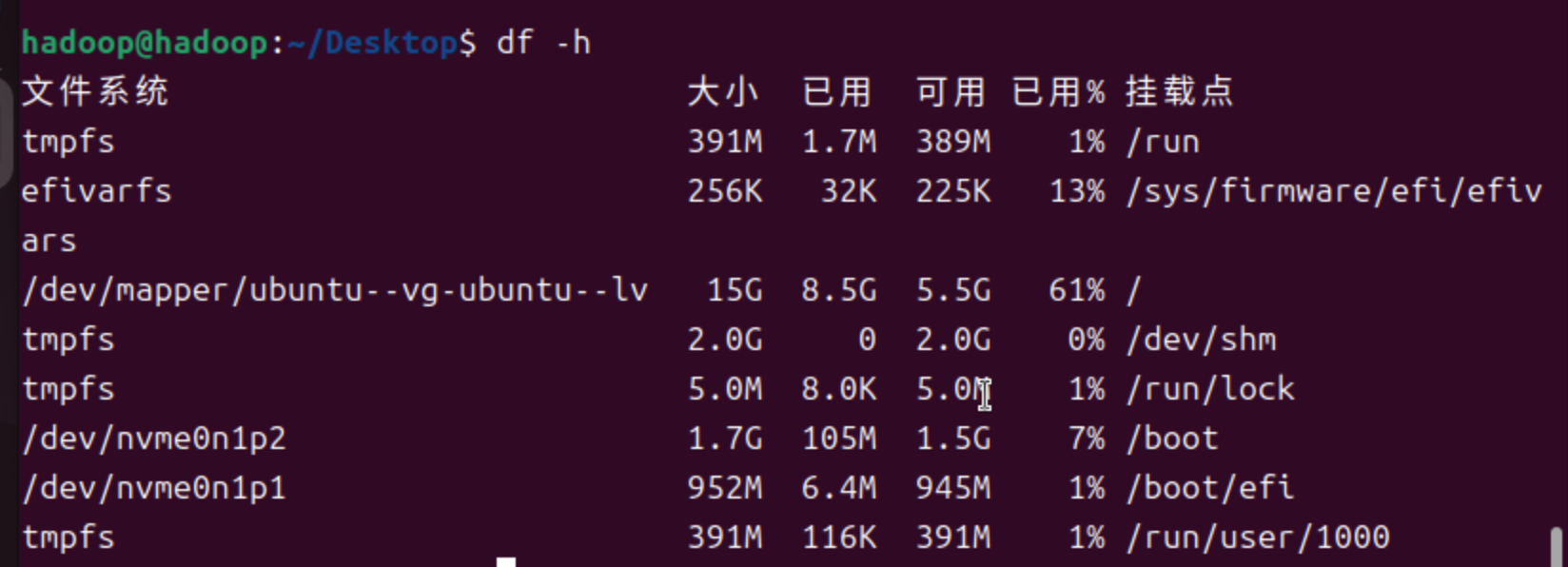
然后确定哪个部分的空间满了:
df -h -
将上一步中占用率较高的一个扩容即可
-
参考如下命令
linuxlvextend -L 10G /dev/mapper/ubuntu--vg-ubuntu--lv //增大或减小至19G lvextend -L +10G /dev/mapper/ubuntu--vg-ubuntu--lv //增加10G lvreduce -L -10G /dev/mapper/ubuntu--vg-ubuntu--lv //减小10G lvresize -l +100%FREE /dev/mapper/ubuntu--vg-ubuntu--lv //按百分比扩容 resize2fs /dev/mapper/ubuntu--vg-ubuntu--lv //执行调整 -
-
扩充后效果如下
-
扩容前,占用率92%
-

-
扩容后,占用61%
-
-
-
-
安装open-vm-tools
linuxsudo apt-get autoremove open-vm-tools sudo apt-get install open-vm-tools sudo apt-get install open-vm-tools-desktop -
配置新镜像源
- 执行如下命令
sudo cp /etc/apt/sources.list.d/ubuntu.sources /etc/apt/sources.list.d/ubuntu.sources.bak sudo vim /etc/apt/sources.list.d/ubuntu.sources- 按照清华源更新,
https://mirrors.tuna.tsinghua.edu.cn/help/ubuntu-ports/- 在ubuntu24以后采用bed822格式,按自己版本配置即可
- 执行如下命令
小结
本周阅读了一篇图结构神经网络相关的论文,该文提出了一种有效的多跳自注意机制------多跳注意图神经网络(MAGNA)。MAGNA使用了一种新颖的图注意力扩散层(图1),首先计算边缘上的注意力权重(用实线箭头表示),然后通过使用边缘上的注意力权重的注意力扩散过程,计算不相连的节点对之间的自注意力权重(虚线箭头)。
参考文献
1\] [Guangtao Wang](https://arxiv.org/search/cs?searchtype=author&query=Wang,+G), [Rex Ying](https://arxiv.org/search/cs?searchtype=author&query=Ying,+R), [Jing Huang](https://arxiv.org/search/cs?searchtype=author&query=Huang,+J), [Jure Leskovec](https://arxiv.org/search/cs?searchtype=author&query=Leskovec,+J); Yang Wang; Fang Chen; Multi-hop Attention Graph Neural Network. https://arxiv.org/abs/2009.14332v5