OpenCV(二十六)：高斯滤波

图像平滑是计算机视觉中的重要基础操作，用于降噪、改善图像质量以及为后续算法（如边缘检测、特征提取、图像金字塔处理等）作准备。在所有平滑方法中，高斯滤波（Gaussian Blur） 是最常用、最经典的一种。与均值滤波或方盒滤波相比，高斯滤波能更好地保护边缘，具有更好的数学性质和视觉效果。

高斯分布（正态分布）

高斯分布是什么？

高斯分布是一种以平均值为中心、呈钟形曲线的概率分布，数据在中心附近最多，越远离中心概率越小。自然界中大量随机现象都服从高斯分布，因此图像处理中常用高斯滤波来模拟自然模糊和消除噪声。

如果一个现象由 许多微小随机因素共同影响，例如：

人的身高
测量误差
传感器噪声
自然界随机变量
图像的噪声（亮度受到电子噪声影响）

那么它最终通常呈现：

中间最多（平均值附近概率最大）
两边逐渐减少
整体形成一个对称的钟形曲线

这就是高斯分布。

你可以把它想象成：

"大部分值都在中间附近，极端值很少。"

高斯分布的数学公式

一维高斯分布公式：

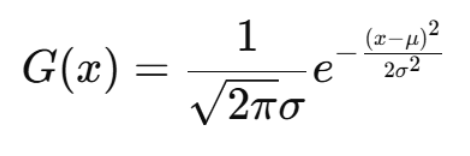
其中：

μ（mu）：平均值（曲线中心位置）
σ（sigma） ：标准差（决定曲线胖瘦）
- σ 小 → 峰窄而高
- σ 大 → 峰宽而低

高斯分布的统计特性

范围	含义
μ ± 1σ	约 68% 的数据落在这里
μ ± 2σ	约 95%
μ ± 3σ	约 99.7%

这就是著名的 "3σ 定律"。

为什么自然界中很多事物呈高斯分布？

因为自然界中的现象通常受大量"微小随机因素"的共同作用。

例如：

身高由基因、营养、生活环境等众多因素影响 → 呈高斯
温度测量误差随机累积 → 呈高斯
图像传感器噪声（电子热噪声） → 高斯噪声

数学上由 中心极限定理 指导：

多个独立随机变量的和趋向于高斯分布。

因此高斯分布几乎无处不在。

图像处理中为什么要使用高斯分布？

图像的噪声常常服从高斯分布，所以高斯滤波是最适合消除噪声的。

高斯滤波使用的权重就是高斯分布：

落在中心的像素影响最大
距离越远权重越小，影响越弱
平滑自然，不破坏结构

而均值滤波会平均所有像素，容易破坏边缘。

因此高斯分布是图像模糊算法中最科学、最合理的选择。

高斯滤波的思想与目的

高斯滤波是一种基于高斯分布（正态分布）权重的平滑方法，它通过给邻域中像素赋予不同权重来实现平滑和降噪。

核心思想：

距离中心越近的像素权重越大，距离越远的权重越小。

相比均值滤波（所有像素权重相同），高斯滤波避免了"丢失边缘特征"问题，因此图像平滑得更自然。

高斯分布服从著名的钟形曲线：

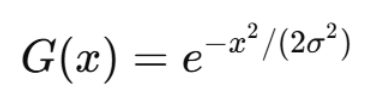
其中 σ 表示标准差，σ 越大，平滑越强。

高斯滤波数学原理

一维高斯函数

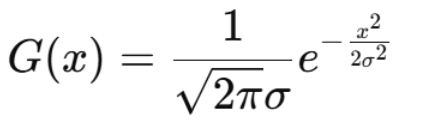
它表示一个以 0 为中心、宽度由 σ 控制的概率密度函数。

二维高斯函数

图像是二维的，因此需要二维高斯核：

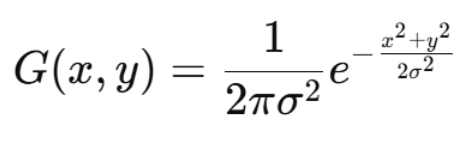
它是一个二维的高斯"钟面"，中心最高，向四周递减。

为什么高斯滤波比均值滤波好？

权重随距离变化更平滑

均值滤波：

所有像素权重相同
会模糊边缘
易丢失图像纹理细节

高斯滤波：

局部像素按照"距离远近"赋权
更接近真实光学成像的模糊方式
边缘保持更好

符合人眼视觉特性

人眼对中心像素更敏感，因此高斯滤波模糊效果更自然。

高斯核可分离（计算速度快）

二维高斯核可以分解为两个一维核：

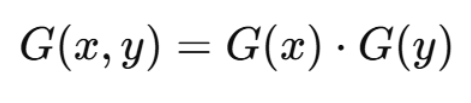
因此复杂度由 O(n²) 降到 O(2n)，OpenCV 内部利用该特性加速。

高斯核（Gaussian Kernel）的生成方法

使用窗口大小 k，与标准差 σ，生成核 K：

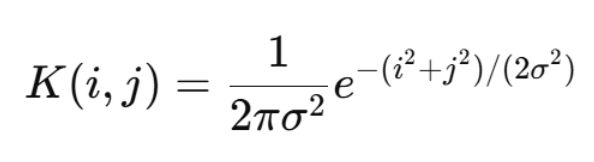
示例：生成 5×5 高斯核（σ=1.0），其权重分布类似：

复制代码

1  4  7  4  1
4 16 26 16  4
7 26 41 26  7
4 16 26 16  4
1  4  7  4  1

然后进行归一化，使核权重和为 1。

高斯滤波的参数与意义（OpenCV）

OpenCV 中高斯滤波函数：

python 复制代码

cv2.GaussianBlur(src, ksize, sigmaX, sigmaY=None, borderType)

参数解释：

参数	含义
src	输入图像
ksize	核大小，例如 (5,5)，必须为奇数
sigmaX	X 方向标准差 σ
sigmaY	Y 方向标准差（不填时自动 = sigmaX）
borderType	边界填充方式

核大小 ksize 必须是奇数的原因

确保存在"唯一中心点"，便于左右对称权重分布。

σ（标准差）的作用

σ 决定模糊程度：

小 → 轻微模糊
大 → 强烈模糊

若设置为 0，OpenCV 会根据核大小自动计算最优 σ。

例如：

ini 复制代码

ksize = 5 → σ ≈ 0.8 ~ 1.0
ksize = 9 → σ ≈ 1.5 ~ 2.0

实际经验：一般使用 σ = 1.0（轻度模糊）。

OpenCV 高斯滤波内部实现机制

OpenCV 高斯滤波主要步骤：

根据 ksize 与 σ 生成一维高斯核 G
使用 separable filter（可分离卷积）
- 先进行 X 方向卷积（行卷积）
- 再进行 Y 方向卷积（列卷积）
使用 SSE/AVX 指令集加速数值运算

可分离卷积使得高斯滤波运行速度比同尺寸的均值滤波更快。

与方盒滤波（boxFilter）对比

过滤类型	权重分布	边缘保留	效果自然度
方盒滤波	全 1	较差	一般
均值滤波	全 1/窗口大小	较差	一般
高斯滤波	随距离变化	较好	最佳

方盒滤波会产生明显模糊，而高斯模糊更柔和。

高斯滤波应用场景

降噪前处理

例如 Canny 边缘检测必须先高斯平滑，以抑制噪声。

图像金字塔

高斯金字塔使用多次高斯滤波 + 下采样构成。

卷积神经网络前处理

改善图像平滑度，提高模型鲁棒性。

模糊效果

用于背景虚化、相机景深模拟。

示例

基本高斯滤波

python 复制代码

import cv2
import numpy as np

# -------------------------------------------------
# 1. 生成一张典型测试图（包含渐变、几何形状、噪声）
# -------------------------------------------------

h, w = 400, 400

# 梯度背景
gradient = np.tile(np.linspace(0, 255, w, dtype=np.uint8), (h, 1))

# 转为 3 通道
img = cv2.merge([gradient, gradient, gradient])

# 画一些形状（增强调试效果）
cv2.rectangle(img, (50, 50), (150, 150), (255, 0, 0), -1)
cv2.circle(img, (300, 100), 50, (0, 255, 0), -1)
cv2.line(img, (200, 200), (350, 350), (0, 0, 255), 5)

# 添加随机噪声
noise = np.random.randint(0, 50, (h, w, 3), dtype=np.uint8)
noisy_img = cv2.add(img, noise)

# -------------------------------------------------
# 2. 高斯滤波
# -------------------------------------------------
sigma = 2.0
gaussian_blur = cv2.GaussianBlur(noisy_img, (0, 0), sigmaX=sigma)

# -------------------------------------------------
# 3. 显示结果
# -------------------------------------------------
cv2.imshow("Original (with noise)", noisy_img)
cv2.imshow(f"Gaussian Blur (sigma={sigma})", gaussian_blur)
cv2.waitKey(0)
cv2.destroyAllWindows()

效果显示：

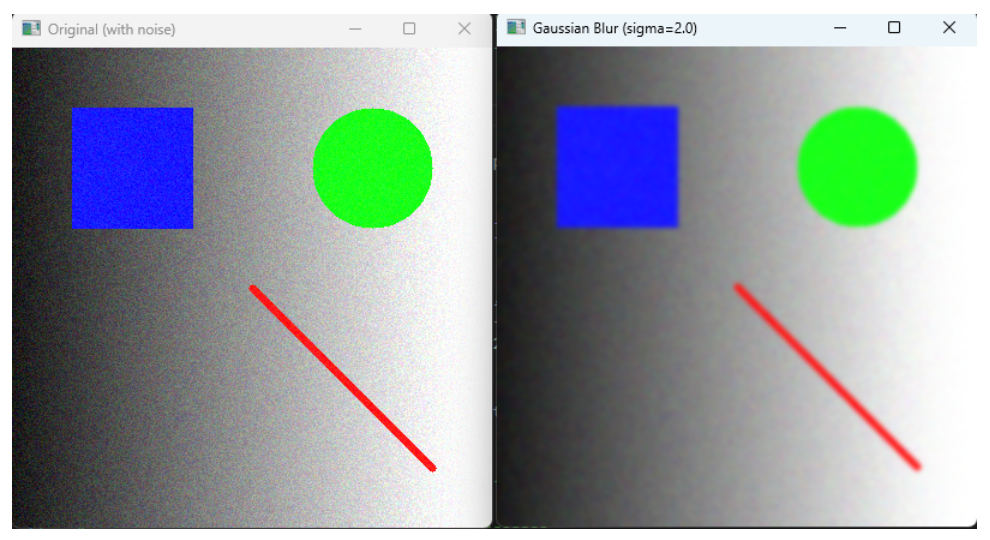
指定 σ 的高斯滤波

python 复制代码

import cv2

img = cv2.imread("test.jpg")

sigma = 2.0  # 指定标准差

# ksize = (0,0) 表示让 OpenCV 根据 sigma 自动计算合适的高斯核大小
blur = cv2.GaussianBlur(img, (0, 0), sigmaX=sigma)

cv2.imshow("Original", img)
cv2.imshow("blur", blur)
cv2.waitKey(0)

对比均值滤波与高斯滤波

python 复制代码

import cv2
import numpy as np

# 读取图像
img = cv2.imread("test.jpg")

# 均值滤波（方框滤波）
mean_blur = cv2.blur(img, (7, 7))      # 或 cv2.boxFilter

# 高斯滤波
gaussian_blur = cv2.GaussianBlur(img, (7, 7), sigmaX=1.5)

# 显示对比
cv2.imshow("Original", img)
cv2.imshow("Mean Blur (7x7)", mean_blur)
cv2.imshow("Gaussian Blur (7x7, sigma=1.5)", gaussian_blur)

cv2.waitKey(0)
cv2.destroyAllWindows()

优点

降噪效果好：比均值滤波更能消除噪声。
边缘保留能力强：权值递减，不破坏结构。
效果自然，不产生块状感。
可分离卷积，运算效率高。
数学性质好，符合物理模型（光学模糊）。

总结

高斯滤波使用二维高斯函数生成权重核，对图像进行加权平均。
权重随距离衰减，使模糊更自然。
核大小必须为奇数。
σ 控制模糊程度。
内部使用可分离卷积提高效率。
应用非常广泛：降噪、边缘检测、图像金字塔等。