深度学习：Adam 优化器实战（Adam Optimizer）

关键词解释： Adam（Adaptive Moment Estimation）优化算法

💡 Adam = Momentum + RMSprop + 偏差修正

它结合了动量的加速能力和自适应学习率的稳定性，是当前深度学习的"默认优化器"。

✅ 一、Adam 的核心思想

Adam 同时维护两个关于梯度的统计量：

一阶矩（均值）：类似动量，记录梯度的历史平均方向；
二阶矩（未中心化的方差）：类似 RMSprop，记录梯度的平方历史，用于自适应缩放学习率。

并通过 偏差修正 解决初期估计偏差问题。

✅ 二、数学公式

对于第 ( t ) 步迭代：

1. 更新移动平均（指数加权）

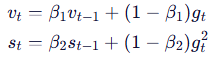
2. 偏差修正（因初始为 0，早期估计偏低）

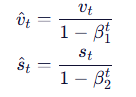
3. 参数更新

其中：

：学习率（如 0.001）；
：一阶矩衰减率；
：二阶矩衰减率；
：防止除零的小常数。

✅ 三、代码实现详解

3.1 初始化 Adam 状态

复制代码

def initialize_adam(parameters):
    L = len(parameters) // 2
    v = {}  # 一阶矩（动量）
    s = {}  # 二阶矩（平方梯度）

    for l in range(L):
        v["dW" + str(l + 1)] = np.zeros_like(parameters["W" + str(l + 1)])
        v["db" + str(l + 1)] = np.zeros_like(parameters["b" + str(l + 1)])
        s["dW" + str(l + 1)] = np.zeros_like(parameters["W" + str(l + 1)])
        s["db" + str(l + 1)] = np.zeros_like(parameters["b" + str(l + 1)])

    return v, s

✅ 作用：为每层权重和偏置初始化 v 和 s 为零矩阵。

3.2 Adam 参数更新函数

复制代码

def update_parameters_with_adam(parameters, grads, v, s, t, learning_rate=0.01,
                                beta1=0.9, beta2=0.999, epsilon=1e-8):
    L = len(parameters) // 2
    v_corrected = {}
    s_corrected = {}

    for l in range(L):
        # 1. 更新一阶矩（动量）
        v["dW" + str(l + 1)] = beta1 * v["dW" + str(l + 1)] + (1 - beta1) * grads['dW' + str(l + 1)]
        v["db" + str(l + 1)] = beta1 * v["db" + str(l + 1)] + (1 - beta1) * grads['db' + str(l + 1)]

        # 2. 偏差修正（一阶矩）
        v_corrected["dW" + str(l + 1)] = v["dW" + str(l + 1)] / (1 - np.power(beta1, t))
        v_corrected["db" + str(l + 1)] = v["db" + str(l + 1)] / (1 - np.power(beta1, t))

        # 3. 更新二阶矩（平方梯度）
        s["dW" + str(l + 1)] = beta2 * s["dW" + str(l + 1)] + (1 - beta2) * np.square(grads['dW' + str(l + 1)])
        s["db" + str(l + 1)] = beta2 * s["db" + str(l + 1)] + (1 - beta2) * np.square(grads['db' + str(l + 1)])

        # 4. 偏差修正（二阶矩）
        s_corrected["dW" + str(l + 1)] = s["dW" + str(l + 1)] / (1 - np.power(beta2, t))
        s_corrected["db" + str(l + 1)] = s["db" + str(l + 1)] / (1 - np.power(beta2, t))

        # 5. 更新参数
        parameters["W" + str(l + 1)] -= learning_rate * v_corrected["dW" + str(l + 1)] / (np.sqrt(s_corrected["dW" + str(l + 1)]) + epsilon)
        parameters["b" + str(l + 1)] -= learning_rate * v_corrected["db" + str(l + 1)] / (np.sqrt(s_corrected["db" + str(l + 1)]) + epsilon)

    return parameters, v, s

✅ 关键点：

使用 np.square() 或 **2 计算梯度平方；

必须传入当前迭代步数 t（从 1 开始计数）；

所有操作按层进行，W 对应 dW，b 对应 db。

✅ 四、测试与输出

复制代码

parameters, grads, v, s = update_parameters_with_adam_test_case()
parameters, v, s = update_parameters_with_adam(parameters, grads, v, s, t=2)

print("W1 =", parameters["W1"])
print("b1 =", parameters["b1"])
print("W2 =", parameters["W2"])
print("b2 =", parameters["b2"])
print("v['dW1'] =", v["dW1"])
print("v['db1'] =", v["db1"])
print("s['dW1'] =", s["dW1"])
print("s['db1'] =", s["db1"])

✅ 预期行为：

所有值均为合理浮点数；
v 接近梯度的加权平均；
s 接近梯度平方的加权平均；
参数更新幅度受 sqrt(s) + ε 自适应调节。

✅ 五、超参数推荐值（Kingma & Ba, 2015）

超参数	默认值	说明
learning_rate (α)	0.001	最关键！常需调参
β₁	0.9	动量衰减率
β₂	0.999	方差衰减率
ε	1e-8	数值稳定常数

💡 注意：

学习率是 Adam 中唯一需要重点调参的超参数；

β₁、β₂ 通常无需修改；

若训练不稳定，可尝试减小学习率或增大 ε。

✅ 六、Adam 的优势与局限

✅ 优势

自适应学习率，对不同参数自动调整；
收敛速度快，适合稀疏梯度（如 NLP）；
对超参数不敏感（除学习率外）；
广泛适用于 CNN、RNN、Transformer 等架构。

⚠️ 局限

内存占用略高（需存储 v 和 s）；
在某些凸优化问题上可能不如 SGD + 动量泛化好；
初期可能收敛过快导致跳过最优解（可通过 warmup 缓解）。

✅ 七、总结

Adam 是现代深度学习的"瑞士军刀" ------ 简单、高效、鲁棒。

"既知道往哪走（动量），又知道走多快（自适应学习率），还懂得起步时要补一补（偏差校正）。"