1. 正运动学理论基础
机器人运动学描述:在机器人的每个关节上D-H参数中的四个参数分别代表关节连杆不同的特征或在进行不同的变换。
本节主要介绍如何采用机器人工具箱Robotics Toolbox对机器人运动学进行分析:
2. 实例
(1)矩阵变换 机器人工具箱用矩阵A表示T,用函数L.A()求出所创建的连杆对象的连杆变换矩阵。
输入matlab命令:
L=Link([0,2, 3,pi/4,0])L.A(O)运行结果:

因此这个变换矩阵为:
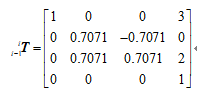
对于给定机器人的连杆,坐标系{i}相对应坐标系的变换是只有一个变量的函数,即旋转关节的关节角qi或移动关节的连杆偏距di。
当上面创建的连杆对象关节角时qi=30,可用L.A()求出相应的变换矩阵。
输入matlab命令:
L.A(pi/6)运行结果为:

求出的相应变换矩阵为
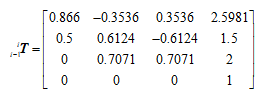
以上推导为前推法,当使用后推法的时候(即从第i-1个关节到第i个关节的变换,与上述变换顺序正好相反),需要采用改进型D-H参数描述法。
在创建连杆对象时,使用改进型D-H描述法需指定参数为modified。
输入matlab命令:
L=Link([0,2,3, pi/4, 0],'modified')运行结果:
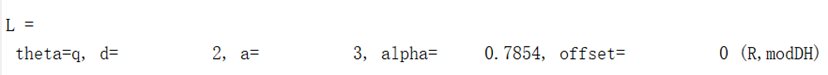
modDH表示使用了改进后D-H参数描述法
输入matlab命令:
L.A(0)运行结果:

所以这个变换矩阵为:
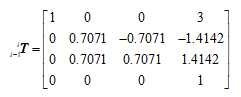
通过将每一个连杆的变换矩阵连乘能够得到坐标{N}相对于坐标{0}的变换矩阵,即:
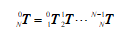
这个变换矩阵是N个关节变量的函数。
回顾前述正运动学的概念:给定一组关节角,计算出工具坐标系相对于基坐标系的位姿。在这里,可以通过各个关节位置传感器得到所需要的值,然后求出每个连杆的变换矩阵,通过上式就可求出机器人末端的工具坐标系相对于基坐标系的位姿,表示为:
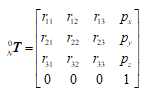
上面的等式中的,即三行三列的子矩阵代表从基座到末端执行器的旋转矩阵,其中每列从左到右分别代表末端执行器描述基座中的x轴、y轴和z轴方向上的单位矢量,即可表示末端执行器基于基座坐标系的方向姿态。而p三行一列从上往下分别代表末端执行器相对于基座坐标系的位置。
(2)正运动学计算 MATLAB机器人工具箱中采用函数fkine()计算正运动学问题。以三连杆平面机器人为例,用标准型D-H参数描述法计算。
输入matlab命令:
L(1)=Link([0,0,1,0])L(2)=Link([0,0,0.8,0])L(3)=Link([0,0,0.6,0])T=three_link.fkine([0 0 0])运行结果:

因此,初始状态的变换矩阵为:
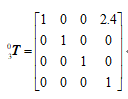
通过输入matlab命令
three_link.plot([0 0 0])可以将创建的机器人用图形化显示出来,运行结果如图1所示。
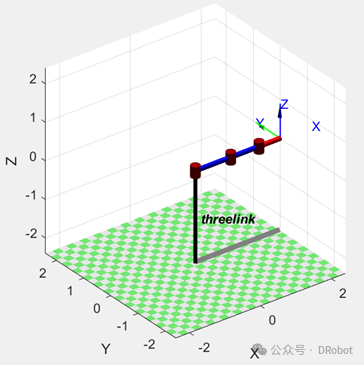
图1 使用标准型D-H参数法创建的机器人
当第二个关节旋转30º,第三个关节旋转45º时;
输入matlab命令:
T=three_link.fkine([0 pi/6 pi/4])运行结果:

输入matlab命令:
three_link.plot([0 pi/6 pi/4])运行结果如图2所示。
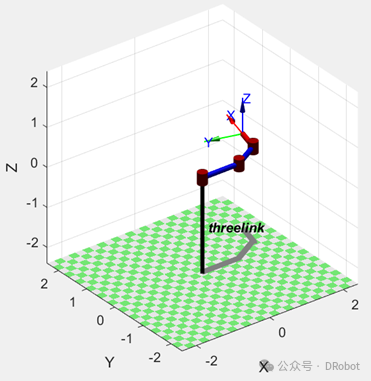
图2 经过旋转变换的机器人