- 模拟退火算法
1.1 算法原理 模拟退火算法的基本思想是从一给定解开始 ,从邻域 中随机产生另一个解 ,接受 Metropolis准则允许目标函数在 有限范围内变坏 ,它由一控制参数 t决定 ,其作用类似于物 理过程中的温度 T,对于控制参数的每一取值 ,算法持续进 行"产生 ---判断 ---接受或舍去 "的迭代过程 ,对应着固体在 某一恒定温度下的趋于热平衡的过程 ,当控制参数逐渐减 小并趋于 0时 ,系统越来越趋于平衡态 ,最后系统状态对应于优化问题的全局最优解 ,该过程也称为冷却过程 ,由于固 体退火必须缓慢降温 ,才能使固体在每一温度下都达到热 平衡 ,最终趋于平衡状态 ,因此控制参数 t经缓慢衰减 ,才 能确保模拟退火算法最终优化问题的整体最优解。
- 2 算法具体步骤
(1)给定模型每一个参数变化范围 ,在这个范围内随 机选择一个初始模型 m0 ,并计算相应的目标函数值 E (m0 )。
(2)对当前模型进行扰动产生一个新模型 m,计算相应 的目标函数值 E (m) ,得到 ΔE = E (m) - E (m0 )。
(3)若 ΔE < 0,则新模型被接受 ;若 ΔE > 0,则新模型 m 按概率 P = exp ( -ΔE/T)进行接受 , T为温度。当模型被接 受时 ,置 m0 =m, E (m0 ) = E (m)。
(4)在温度 T下 ,重复一定次数的扰动和接受过程 ,即 重复步骤 (2)、(3)。
(5)缓慢降低温度 T。
(6)重复步骤 (2)、(5) ,直至收敛条件满足为止。
算法的实质分两次循环 ,随机扰动产生新模型并计算 目标函数值 (或称能量 )的变化 ,决定是否被接受。由于算 法初始温度设计在高温条件 ,这使得 E增大的模型可能被 接受 ,因而能舍去局部极小值 ,通过缓慢地降低温度 ,算法 最终能收敛到全局最优点。
实验用例:用模拟退火算法解决如下 10 个城市的 TSP 问题(Traveling Salesman Problem,旅行商问题),由威廉哈密顿爵士和英国数学家克克曼T.P.Kirkman于19世纪初提出。 问题描述如下: 有若干个城市,任何两个城市之间的距离都是确定的,现要求一旅行商从某城市出发必须经过每一个城市且只在一个城市逗留一次,最后回到出发的城市,问如何事先确定一条最短的线路已保证其旅行的费用最少?),该问题最优解为 f_opt = 2.691。

编程实现
用 MATLAB 实现模拟退火算法时,共编制了 5 个 m 文件,分别如下
-
swap.m
function [ newpath , position ] = swap( oldpath , number )% 对 oldpath 进 行 互 换 操 作% number 为 产 生 的 新 路 径 的 个 数% position 为 对 应 newpath 互 换 的 位 置m = length( oldpath ) ; % 城 市 的 个 数newpath = zeros( number , m ) ;position = sort( randi( m , number , 2 ) , 2 ); % 随 机 产 生 交 换 的 位 置for i = 1 : number newpath( i , : ) = oldpath ;% 交 换 路 径 中 选 中 的 城 市 newpath( i , position( i , 1 ) ) = oldpath( position( i , 2 ) ) ; newpath( i , position( i , 2 ) ) = oldpath( position( i , 1 ) ) ;end
2.pathfare.m
function [ objval ] = pathfare( fare , path )% 计 算 路 径 path 的 代 价 objval% path 为 1 到 n 的 排 列 ,代 表 城 市 的 访 问 顺 序 ;% fare 为 代 价 矩 阵 , 且 为 方 阵 。[ m , n ] = size( path ) ;objval = zeros( 1 , m ) ;for i = 1 : m for j = 2 : n objval( i ) = objval( i ) + fare( path( i , j - 1 ) , path( i , j ) ) ; end objval( i ) = objval( i ) + fare( path( i , n ) , path( i , 1 ) ) ;end3、distance.m
function [ fare ] = distance( coord )% 根 据 各 城 市 的 距 离 坐 标 求 相 互 之 间 的 距 离% fare 为 各 城 市 的 距 离 , coord 为 各 城 市 的 坐 标[ ~ , m ] = size( coord ) ; % m 为 城 市 的 个 数fare = zeros( m ) ;for i = 1 : m % 外 层 为 行 for j = i : m % 内 层 为 列 fare( i , j ) = ... ( sum( ( coord( : , i ) - coord( : , j ) ) .^ 2 ) ) ^ 0.5 ; fare( j , i ) = fare( i , j ) ; % 距 离 矩 阵 对 称 endend4、myplot.m
function [ ] = myplot( path , coord , pathfar )% 做 出 路 径 的 图 形% path 为 要 做 图 的 路 径 ,coord 为 各 个 城 市 的 坐 标% pathfar 为 路 径 path 对 应 的 费 用len = length( path ) ;clf ;hold on ;title( [ '近似最短路径如下,费用为' , num2str( pathfar ) ] ) ;plot( coord( 1 , : ) , coord( 2 , : ) , 'ok');pause( 0.4 ) ;for ii = 2 : len plot( coord( 1 , path( [ ii - 1 , ii ] ) ) , coord( 2 , path( [ ii - 1 , ii ] ) ) , '-b'); x = sum( coord( 1 , path( [ ii - 1 , ii ] ) ) ) / 2 ; y = sum( coord( 2 , path( [ ii - 1 , ii ] ) ) ) / 2 ; text( x , y , [ '(' , num2str( ii - 1 ) , ')' ] ) ; pause( 0.4 ) ;endplot( coord( 1 , path( [ 1 , len ] ) ) , coord( 2 , path( [ 1 , len ] ) ) , '-b' ) ;x = sum( coord( 1 , path( [ 1 , len ] ) ) ) / 2 ;y = sum( coord( 2 , path( [ 1 , len ] ) ) ) / 2 ;text( x , y , [ '(' , num2str( len ) , ')' ] ) ;pause( 0.4 ) ;hold off ;5、mySAA.m
% 模 拟 退 火 算 法 ( Simulated Annealing Algorithm ) MATLAB 程 序clear ;% 程 序 参 数 设 定Coord = ... % 城 市 的 坐 标 Coordinates [ 0.6683 0.6195 0.4 0.2439 0.1707 0.2293 0.5171 0.8732 0.6878 0.8488 ; ... 0.2536 0.2634 0.4439 0.1463 0.2293 0.761 0.9414 0.6536 0.5219 0.3609 ] ;t0 = 1 ; % 初 温 t0iLk = 20 ; % 内 循 环 最 大 迭 代 次 数 iLkoLk = 50 ; % 外 循 环 最 大 迭 代 次 数 oLklam = 0.95 ; % λ lambdaistd = 0.001 ; % 若 内 循 环 函 数 值 方 差 小 于 istd 则 停 止ostd = 0.001 ; % 若 外 循 环 函 数 值 方 差 小 于 ostd 则 停 止ilen = 5 ; % 内 循 环 保 存 的 目 标 函 数 值 个 数olen = 5 ; % 外 循 环 保 存 的 目 标 函 数 值 个 数% 程 序 主 体m = length( Coord ) ; % 城 市 的 个 数 m fare = distance( Coord ) ; % 路 径 费 用 farepath = 1 : m ; % 初 始 路 径 pathpathfar = pathfare( fare , path ) ; % 路 径 费 用 path fareores = zeros( 1 , olen ) ; % 外 循 环 保 存 的 目 标 函 数 值e0 = pathfar ; % 能 量 初 值 e0t = t0 ; % 温 度 tfor out = 1 : oLk % 外 循 环 模 拟 退 火 过 程 ires = zeros( 1 , ilen ) ; % 内 循 环 保 存 的 目 标 函 数 值 for in = 1 : iLk % 内 循 环 模 拟 热 平 衡 过 程 [ newpath , ~ ] = swap( path , 1 ) ; % 产 生 新 状 态 e1 = pathfare( fare , newpath ) ; % 新 状 态 能 量 % Metropolis 抽 样 稳 定 准 则 r = min( 1 , exp( - ( e1 - e0 ) / t ) ) ; if rand < r path = newpath ; % 更 新 最 佳 状 态 e0 = e1 ; end ires = [ ires( 2 : end ) e0 ] ; % 保 存 新 状 态 能 量 % 内 循 环 终 止 准 则 :连 续 ilen 个 状 态 能 量 波 动 小 于 istd if std( ires , 1 ) < istd break ; end end ores = [ ores( 2 : end ) e0 ] ; % 保 存 新 状 态 能 量% 外 循 环 终 止 准 则 :连 续 olen 个 状 态 能 量 波 动 小 于 ostd if std( ores , 1 ) < ostd break ; end t = lam * t ; endpathfar = e0 ;% 输 入 结 果fprintf( '近似最优路径为:\n ' )%disp( char( [ path , path(1) ] + 64 ) ) ;disp(path)fprintf( '近似最优路径费用\tpathfare=' ) ;disp( pathfar ) ;myplot( path , Coord , pathfar ) ;
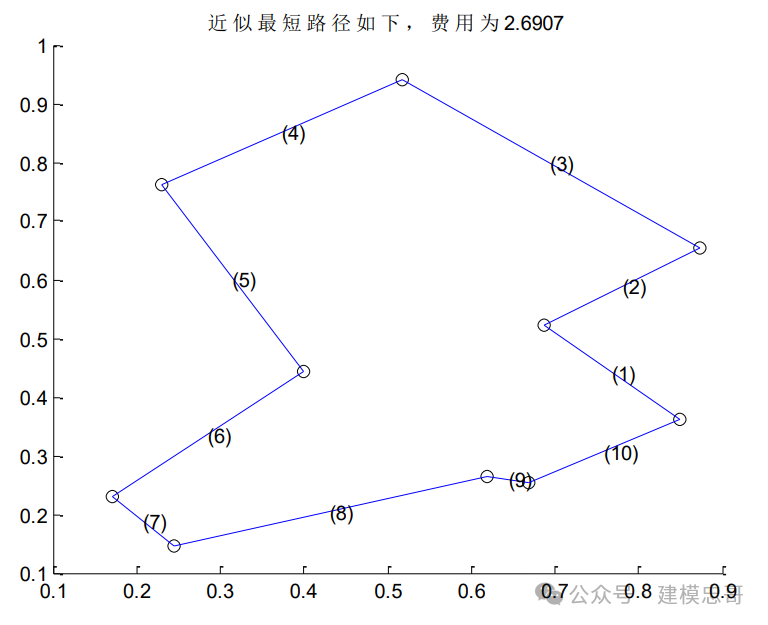
我试着运行了几次(只是改变了一下初温,也可以更改一下其他参数),发现初始温度 t0=1 时程序的最后结果与最优解差距小的概率比较大。 希望对大家有用!!