21. Revit API: 几何对象（二）- Curve

上篇讲了Revit几何对象的类层次结构，讲了几何元素和几何实例，简单提到了Solid。

这一篇呢，就从构成Solid的边讲起。

一、Edge（边）

Edge在Revit中就是用来表示边的，并且在各种表示几何结构的类中串门。

前面说，Solid是由Edge和Face组成的。从Solid上拿到的是Edge的集合EdgeArray。

P.S. 看到这个EdgeArray，就去到app上看看能不能创建，发现有CurveArray，没有这个。

行吧，没有就没有，老老实实new一个吧。

Edge简单理解就是套了层壳的Curve。其上的大部分方法、属性和Curve是一样的。

当然了，由于边是"具体"的，线是"逻辑"的，所以边上有个别与面相关的方法这些就都不展开了。

csharp 复制代码

var curve = edge.AsCurve(); // 获取描述Edge的曲线

二、Curve

Curve就是曲线，各种线（6类）的基类。

Curve 能做啥？

2.1. 曲线的作用

曲线之间的关系
a. 两条曲线的相交
b. 两条曲线之间最短距离的点
点与曲线的关系
a. 点是否在曲线上
b. 点在曲线上的投影
曲线自身
a. 获取曲线上某处的点坐标
b. 曲线细分，点集化
c. 长度、是否循环、是否有界
d. 样式
曲线的创建
a. 翻转
b. Transform变换
c. 偏移

有3个重点：① 曲线上点的获取，② 曲线的样式设置，③ 曲线的偏移

样式后面专门介绍。

2.2. 偏移原理

Curve上有一个CreateOffset(..)方法，用于创建一个偏移后的曲线。

csharp 复制代码

// offsetDist：距离
// referenceVector：方向
public Curve CreateOffset(double offsetDist,XYZ referenceVector)

之前有写过一篇关于CurveLoop的笔记。有讲Curveloop的偏移，就是对里面每个Curve进行偏移。

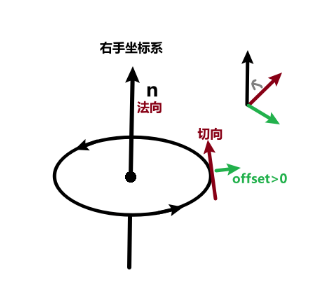
偏移方向为：线的切向量与指定方向向量的叉乘的方向。

所以：

切向量与指定方向向量同向时，偏移为0。
平移操作，使用CreateTransformed(..)代替，传入平移变换矩阵。

2.3. 曲线参数解释

许多几何库的曲线都有这么个东西：曲线的参数化值（the value of the parameter ）。

当把曲线看作由一个函数定义，拿函数中有变量$ u ，通过改变，通过改变，通过改变 u $，就能得到曲线上不同位置的点。

这个值可以是"标准化"的，即值在区间[0,1]内。也可以是任意的。

有界的曲线，才能获取端点

参数的起始值可能是任何值，这是比较奇怪的地方，它是由Revit决定的。通过函数GetEndParameter(0/1)获取。

csharp 复制代码

var startParameter = curve.GetEndParameter(0);
var endParameter = curve.GetEndParameter(1);
var length = endParameter - startParameter; //  curve.ApproximateLength;
// 起点与重点的参数差，正好是曲线的长度（未标准化）

那么，可以这样获取曲线上的点：

csharp 复制代码

 // 获取 曲线的中间点
 var center = curve.Evaluate(0.5, true);  // 标准化参数
 // 获取 离曲线起点 1/2 长度的点
 var center2 = curve.Evaluate(startParameter + length / 2, false);  // 原始参数

原始参数和标准化参数之间可以相互转换。

虽然了解了这些后，我们可以自己写一个转换方法，但Curve上已经提供了。

csharp 复制代码

var rawParameter = curve.ComputeRawParameter(0.5);  // == startParameter + length / 2
var normalizedParameter = curve.ComputeNormalizedParameter(startParameter + length / 2);  // 0.5

Curve 上还有个比较有用的方法ComputeDerivatives(..)，它计算后返回一个Transform类型的结果。

transform.Origin：点，相当于Evaluate(...)
transform.BaseX：切向量（一阶导）
transform.BaseY：二阶导
transform.BaseZ：双法向量（切向量 x 法向量）

三、Curve 派生类

3.1. Line（直线）

由起点、方向定义。

可由两点构造有界直线，或起点+方向构造无界直线。

略

3.2. Arc（圆弧）

由中心、半径，法向、X向、Y向定义。

后面三个，用来确定坐标系。

但有点奇怪的是，看不到圆弧转过的弧度（没有弧度属性），这个需要通过计算才能得到。

emm...奇怪。

csharp 复制代码

// 计算圆弧的弧度
var dir1 = arc.Evaluate(0, true) - arc.Center;  // 圆心到弧起点
var dir2 = arc.Evaluate(1, true) - arc.Center;  // 圆心到弧终点
var red = Vector2.a

3.3. Ellipse（椭圆）

由中心、X半径、Y半径，法向，X向，Y向定义。

后三个，依旧是确定坐标系。

当X半径与Y半径相等时，就是一个圆了。

3.4. CylindricalHelix（螺旋线）

弹簧玩过没有，那就是个CylindricalHelix。

这里是Wiki，或者看这里。

我就跳过了嗷，太菜了，看不懂。

3.5. HermiteSpline 和 NurbSpline

"叮又叮不懂，鞋又鞋不废".jpg

用倒是直接用，没毛病。·

至于其函数定义，实现方式，以后再看吧。插眼。

四、总结

这篇是在很久之前写的，后面还写了篇关于IUpdater 的，都没有发出来。

Revit没有在看了，最近在看SolidWorks，然后看着也烦，就写了几何对象（三），这篇就发出来吧。