代码随想录算法训练营day18|二叉树06

一、530.二叉搜索树的最小绝对差

530. 二叉搜索树的最小绝对差 - 力扣（LeetCode）

给你一棵所有节点为非负值的二叉搜索树，请你计算树中任意两节点的差的绝对值的最小值。

示例：

提示：树中至少有 2 个节点

思路：

class Solution:
    def __init__(self):
        self.vec = []

    def traversal(self, root):
        if root is None:
            return
        self.traversal(root.left)
        self.vec.append(root.val)  # 将二叉搜索树转换为有序数组
        self.traversal(root.right)

    def getMinimumDifference(self, root):
        self.vec = []
        self.traversal(root)
        if len(self.vec) < 2:
            return 0
        result = float('inf')
        for i in range(1, len(self.vec)):
            # 统计有序数组的最小差值
            result = min(result, self.vec[i] - self.vec[i - 1])
        return result

二、501.二叉搜索树中的众数

501. 二叉搜索树中的众数 - 力扣（LeetCode）

给定一个有相同值的二叉搜索树（BST），找出 BST 中的所有众数（出现频率最高的元素）。

假定 BST 有如下定义：

• 结点左子树中所含结点的值小于等于当前结点的值
• 结点右子树中所含结点的值大于等于当前结点的值
• 左子树和右子树都是二叉搜索树

例如：

给定 BST [1,null,2,2],

返回[2].

提示：如果众数超过1个，不需考虑输出顺序

思路：

1、当作普通二叉树进行搜索

先进行遍历，此处用的是前序，统计所有元素的频率def searchBST(self, cur, freq_map):

把统计出来的出现频率，利用字典key：元素，value：出现频率进行排序

取前面高频的元素

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
from collections import defaultdict

class Solution:
    def searchBST(self, cur, freq_map):
        if cur is None:
            return
        freq_map[cur.val] += 1  # 统计元素频率
        self.searchBST(cur.left, freq_map)
        self.searchBST(cur.right, freq_map)

    def findMode(self, root):
        freq_map = defaultdict(int)  # key:元素，value:出现频率
        result = []
        if root is None:
            return result
        self.searchBST(root, freq_map)
        max_freq = max(freq_map.values())
        for key, freq in freq_map.items():
            if freq == max_freq:
                result.append(key)
        return result

2、考虑二叉搜索树，中序遍历为有序的

class Solution:
    def __init__(self):
        self.maxCount = 0  # 最大频率
        self.count = 0  # 统计频率
        self.pre = None
        self.result = []

    def searchBST(self, cur):
        if cur is None:
            return

        self.searchBST(cur.left)  # 左
        # 中
        if self.pre is None:  # 第一个节点
            self.count = 1
        elif self.pre.val == cur.val:  # 与前一个节点数值相同
            self.count += 1
        else:  # 与前一个节点数值不同
            self.count = 1
        self.pre = cur  # 更新上一个节点

        if self.count == self.maxCount:  # 如果与最大值频率相同，放进result中
            self.result.append(cur.val)

        if self.count > self.maxCount:  # 如果计数大于最大值频率
            self.maxCount = self.count  # 更新最大频率
            self.result = [cur.val]  # 很关键的一步，不要忘记清空result，之前result里的元素都失效了

        self.searchBST(cur.right)  # 右
        return

    def findMode(self, root):
        self.count = 0
        self.maxCount = 0
        self.pre = None  # 记录前一个节点
        self.result = []

        self.searchBST(root)
        return self.result

三、236. 二叉树的最近公共祖先

236. 二叉树的最近公共祖先 - 力扣（LeetCode）

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为："对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。"

例如，给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]

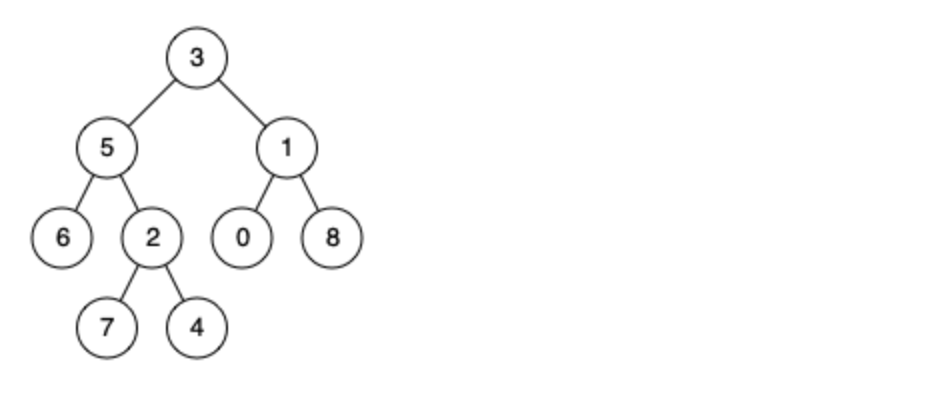
示例 1: 输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出: 3 解释: 节点 5 和节点 1 的最近公共祖先是节点 3。

示例 2: 输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出: 5 解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。

说明:

• 所有节点的值都是唯一的。
• p、q 为不同节点且均存在于给定的二叉树中。

思路：

接下来就看如何判断一个节点是节点q和节点p的公共祖先呢。

首先最容易想到的一个情况：如果找到一个节点，发现左子树出现结点p，右子树出现节点q，或者 左子树出现结点q，右子树出现节点p，那么该节点就是节点p和q的最近公共祖先。

1. 求最小公共祖先，需要从底向上遍历，那么二叉树，只能通过后序遍历（即：回溯）实现从底向上的遍历方式。

2. 在回溯的过程中，必然要遍历整棵二叉树，即使已经找到结果了，依然要把其他节点遍历完，因为要使用递归函数的返回值（也就是代码中的left和right）做逻辑判断。

3. 要理解如果返回值left为空，right不为空为什么要返回right，为什么可以用返回right传给上一层结果。

递归三部曲：

• 确定递归函数返回值以及参数

需要递归函数返回值，来告诉我们是否找到节点q或者p，那么返回值为bool类型就可以了。

但我们还要返回最近公共节点，可以利用上题目中返回值是TreeNode * ，那么如果遇到p或者q，就把q或者p返回，返回值不为空，就说明找到了q或者p。

• 确定终止条件

遇到空的话，因为树都是空了，所以返回空。

那么我们来说一说，如果 root == q，或者 root == p，说明找到 q p ，则将其返回，这个返回值，后面在中节点的处理过程中会用到，那么中节点的处理逻辑，下面讲解。

• 确定单层递归逻辑

值得注意的是 本题函数有返回值，是因为回溯的过程需要递归函数的返回值做判断，但本题我们依然要遍历树的所有节点。

在递归函数有返回值的情况下：如果要搜索一条边，递归函数返回值不为空的时候，立刻返回，如果搜索整个树，直接用一个变量left、right接住返回值，这个left、right后序还有逻辑处理的需要，也就是后序遍历中处理中间节点的逻辑（也是回溯）。

那么为什么要遍历整棵树呢？直观上来看，找到最近公共祖先，直接一路返回就可以了。

如图：

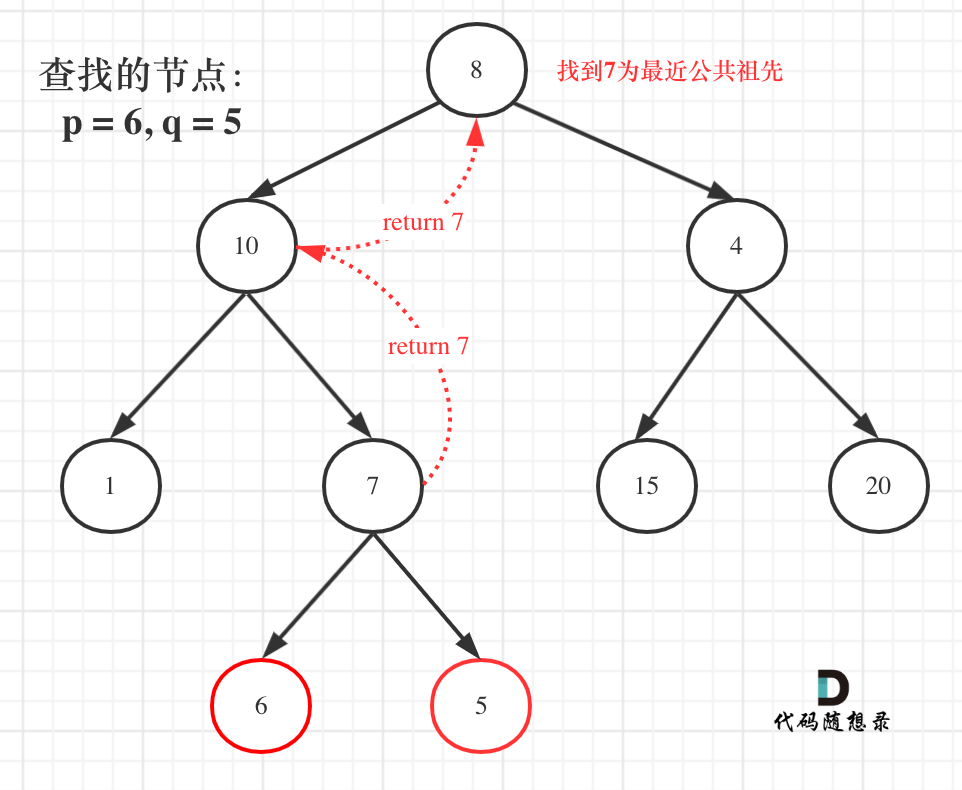
就像图中一样直接返回7。

但事实上还要遍历根节点右子树（即使此时已经找到了目标节点了），也就是图中的节点4、15、20。

因为在如下代码的后序遍历中，如果想利用left和right做逻辑处理， 不能立刻返回，而是要等left与right逻辑处理完之后才能返回。

left = 递归函数(root->left);  // 左
right = 递归函数(root->right); // 右
left与right的逻辑处理;         // 中 

1

2

3

所以此时大家要知道我们要遍历整棵树。知道这一点，对本题就有一定深度的理解了。

那么先用left和right接住左子树和右子树的返回值，代码如下：

TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);

1

2

3

如果left 和 right都不为空，说明此时root就是最近公共节点。这个比较好理解

如果left为空，right不为空，就返回right，说明目标节点是通过right返回的，反之依然。

这里有的同学就理解不了了，为什么left为空，right不为空，目标节点通过right返回呢？

如图：

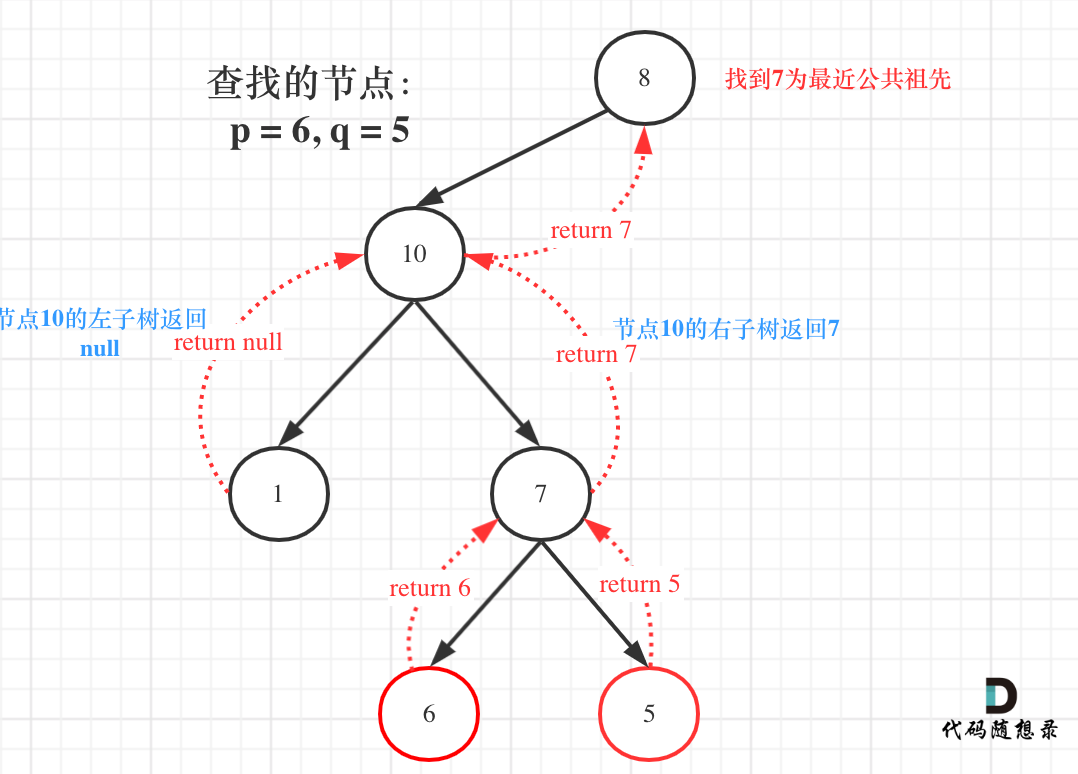
图中节点10的左子树返回null，右子树返回目标值7，那么此时节点10的处理逻辑就是把右子树的返回值（最近公共祖先7）返回上去！

这里也很重要，可能刷过这道题目的同学，都不清楚结果究竟是如何从底层一层一层传到头结点的。

那么如果left和right都为空，则返回left或者right都是可以的，也就是返回空。

class Solution:
    def lowestCommonAncestor(self, root, p, q):
        if root == q or root == p or root is None:
            return root

        left = self.lowestCommonAncestor(root.left, p, q)
        right = self.lowestCommonAncestor(root.right, p, q)

        if left is not None and right is not None:
            return root

        if left is None and right is not None:
            return right
        elif left is not None and right is None:
            return left
        else: 
            return None

精简：

class Solution:
    def lowestCommonAncestor(self, root, p, q):
        if root == q or root == p or root is None:
            return root

        left = self.lowestCommonAncestor(root.left, p, q)
        right = self.lowestCommonAncestor(root.right, p, q)

        if left is not None and right is not None:
            return root

        if left is None:
            return right
        return left