目录
[题目:卡码网 117. 软件构建](#题目:卡码网 117. 软件构建)
[题解:拓扑排序 - Kahn算法(BFS)](#题解:拓扑排序 - Kahn算法(BFS))
一、拓扑排序介绍
对于拓扑排序,可以看看b站这个视频了解一下基本原理:图-拓扑排序
定义
拓扑排序(Topological Sorting)是对有向无环图 (Directed Acyclic Graph,简称DAG)进行排序的一种算法。在图论中,拓扑排序为一个线性序列,这个序列满足对于每一条有向边(u, v),u在序列中都出现在v之前。换句话说,拓扑排序是对有向图顶点的一种线性排序,使得对于每一条有向边(u, v),u在排序中都在v之前。
特点
一、有向无环图:拓扑排序只适用于DAG,如果图中存在环,则无法进行拓扑排序。(故可以通过拓扑排序检查图中是否存在环)
二、线性序列:拓扑排序的结果是一个线性的序列,满足边的方向性要求。
三、唯一性:一个DAG可能有多个拓扑排序序列。
实现方法(2种)
-
Kahn算法(BFS):
- 计算所有顶点的入度。
- 将所有入度为0的顶点入队。
- 当队列非空时:
- 从队列中取出一个顶点,将其添加到拓扑序列中。
- 减少其所有出边指向的顶点的入度。
- 如果某个顶点的入度变为0,将其入队。
-
深度优先搜索(DFS):
- 对于每个顶点,如果它没有被访问过,从它开始进行深度优先搜索。
- 在DFS结束时,将该顶点添加到拓扑序列的开始位置。
- 重复上述过程,直到所有的顶点都被访问过。
应用
-
项目调度:(1)在项目管理中,确定任务执行的顺序,使得所有前置任务都完成后才开始后续任务。 (2)在敏捷开发或瀑布模型中,确定各个阶段的完成顺序。
-
课程安排:在大学课程设计中,确定课程的学习顺序,考虑到某些课程是其他课程的前提条件。
-
编译依赖:在编译大型软件项目时,确定源文件的编译顺序,以确保所有依赖关系都得到满足。
-
任务优先级:在操作系统中,确定进程或线程的执行顺序,考虑到某些任务必须在其他任务之后执行。
-
网站链接结构分析:确定网页之间的链接关系,用于搜索引擎优化或网站导航设计。
-
事件序列化:在日志分析中,确定事件发生的先后顺序,特别是当事件之间存在因果关系时。
-
文件依赖解析:在文件系统或版本控制系统中,确定文件修改的顺序,以避免冲突和错误。
-
有向无环图分析:在任何DAG(有向无环图)的分析中,确定顶点的一个线性序列,使得对于每一条有向边(u, v),u在序列中都出现在v之前。
-
层次结构排序:确定组织结构或分类层次中的元素的顺序,如公司员工、产品类别等。
二、题目与题解
题目:卡码网 117. 软件构建
题目链接
题目描述
某个大型软件项目的构建系统拥有 N 个文件,文件编号从 0 到 N - 1,在这些文件中,某些文件依赖于其他文件的内容,这意味着如果文件 A 依赖于文件 B,则必须在处理文件 A 之前处理文件 B (0 <= A, B <= N - 1)。请编写一个算法,用于确定文件处理的顺序。
输入描述
第一行输入两个正整数 N, M。表示 N 个文件之间拥有 M 条依赖关系。
后续 M 行,每行两个正整数 S 和 T,表示 T 文件依赖于 S 文件。
输出描述
输出共一行,如果能处理成功,则输出文件顺序,用空格隔开。
如果不能成功处理(相互依赖),则输出 -1。
输入示例
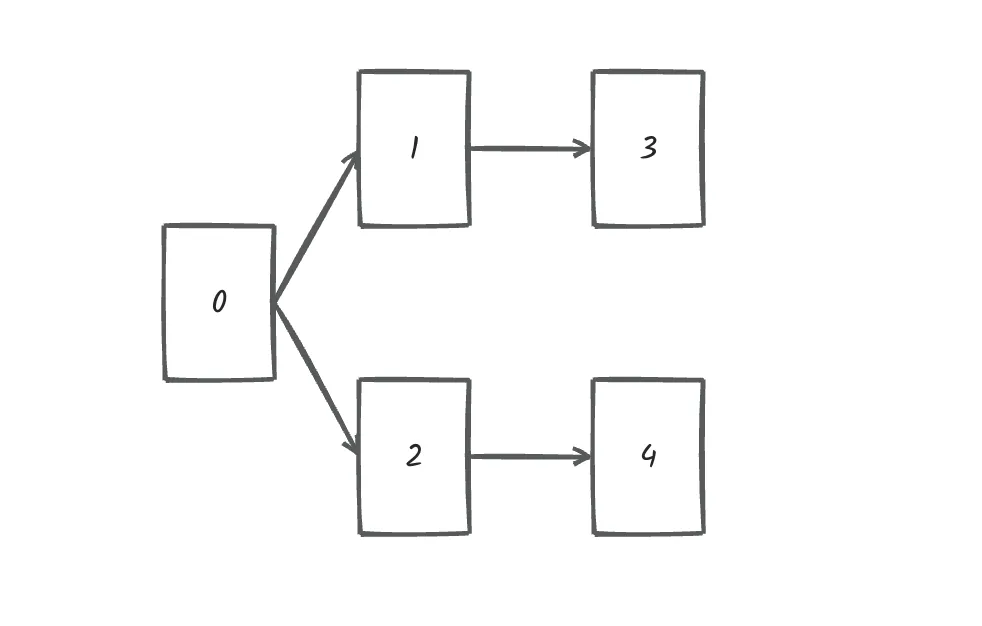
5 4 0 1 0 2 1 3 2 4输出示例
0 1 2 3 4提示信息
文件依赖关系如下:
所以,文件处理的顺序除了示例中的顺序,还存在
0 2 4 1 3
0 2 1 3 4
等等合法的顺序。
数据范围:
0 <= N <= 10 ^ 5
1 <= M <= 10 ^ 9
每行末尾无空格。
题解:拓扑排序 - Kahn算法(BFS)
这题是拓扑排序一个基本的应用:文件依赖问题。
Kahn算法的基本思路:
- 计算所有顶点的入度。
- 将所有入度为0的顶点入队。
- 当队列非空时:
- 从队列中取出一个顶点,将其添加到拓扑序列中。
- 减少其所有出边指向的顶点的入度。
- 如果某个顶点的入度变为0,将其入队。
代码如下:
cpp
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n, m; // n表示文件数量,m表示依赖关系的数量
cin >> n >> m;
vector<int> inDegree(n, 0); // 初始化所有文件的入度为0
// 使用哈希表存储文件依赖关系,键(key)为文件编号,值(value)为依赖于该文件的文件列表
unordered_map<int, vector<int>> dependencies;
vector<int> ans; // 用于存储拓扑排序的结果
// 读取依赖关系并构建依赖图
for (int i = 0; i < m; i++)
{
int s, t;
cin >> s >> t;
inDegree[t]++; // 文件t依赖于文件s,因此文件t的入度增加
dependencies[s].push_back(t); // 记录文件s的依赖列表
}
// 初始化队列,将所有入度为0的文件加入队列
queue<int> q;
for (int i = 0; i < n; ++i)
{
if (inDegree[i] == 0)
{
q.push(i);
}
}
// 进行拓扑排序
while (!q.empty())
{
int cur = q.front(); // 取出当前入度为0的文件
q.pop();
ans.push_back(cur); // 将其加入拓扑排序结果中
for (int next : dependencies[cur]) // 遍历当前文件依赖的所有文件
{
--inDegree[next]; // 减少依赖文件的入度
if (inDegree[next] == 0) // 如果入度变为0,说明所有依赖的文件都已经处理过,可以将其加入队列
{
q.push(next);
}
}
}
// 检查是否所有文件都已处理,如果没有,说明存在循环依赖
if (ans.size() == n)
{
// 输出拓扑排序结果
for (int i = 0; i < ans.size(); ++i)
{
cout << ans[i];
if (i < ans.size() - 1)
{
cout << " "; // 在文件编号之间添加空格,最后一个文件后不加空格(特别注意)
}
}
}
else // 如果结果集大小不等于文件数量,说明存在循环依赖
{
cout << -1 << endl;
}
return 0;
}这题当然也可以通过DFS实现,即是采用递归的思路,这里就不过多介绍了。对于拓扑排序问题,一般选择Kahn算法。
三、小结
最近图论章节的难度较大,打卡有延误。不过训练营的打卡也快要结束了,后边会继续加油打卡!