图论\dp 两题 - 技术栈

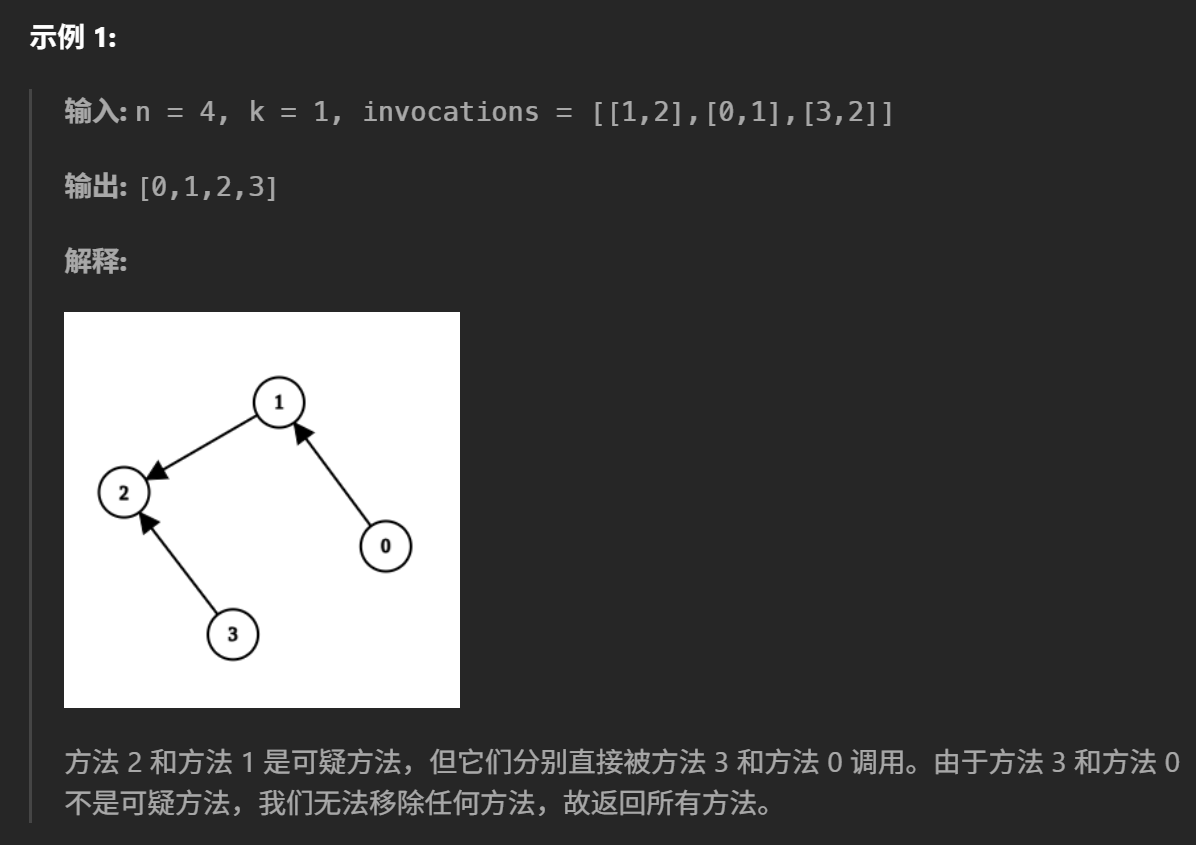
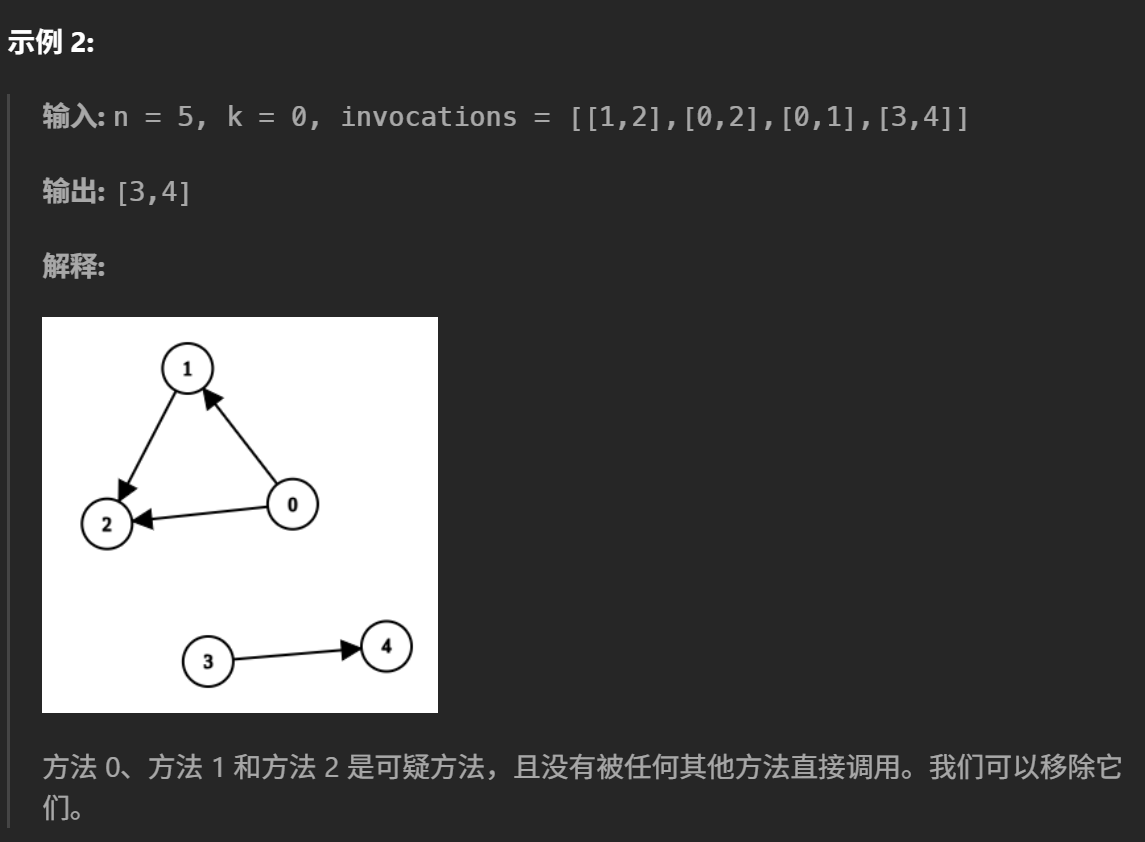
读懂题目就不难。 $a,b$ 表示方法a调用了方法b。现在要除去所有的可疑方法，就要把方法k调用的（直接与间接）方法都删除。如果存在非可疑方法调用可疑方法，就不删除任何方法。

思路很简单，建图之后从k开始搜索。dfs或者bfs都可以。注意，有向图没办法用并查集。用并查集判断了k和哪些节点是在一个集合中，但没办法处理这个集合中节点的指向关系。

bfs版本：

cpp 复制代码

class Solution
{
public:
    vector<int> remainingMethods(int n, int k, vector<vector<int>>& invocations)
    {
        //建图
        vector<vector<int>>g(n);
        for (auto& edge:invocations)
        {
            g[edge[0]].push_back(edge[1]);
        }
        //方法edge[0]调用了方法edge[1]

        //bfs找出可疑方法：方法k及其调用的方法
        vector<int>sus(n);
        queue<int>que;
        que.push(k);//从k开始bfs
        sus[k] = 1;//可疑标记为1
        while (!que.empty())
        {
            int curr = que.front();
            que.pop();
            for (int node : g[curr])
            {
                if (sus[node] == 0)//图可能有环，避免死循环
                {
                    sus[node] = 1;
                    que.push(node);
                }
            }
        }

        //检查：是否有非可疑方法调用可以方法，如果有就不能删掉
        for (auto& e : invocations)
        {
            if (sus[e[0]] == 0 && sus[e[1]] == 1)//非可疑方法调用可疑方法
            {
                //则无法移除可疑方法
                vector<int>ans(n);
                iota(ans.begin(), ans.end(), 0);
                return ans;
            }
        }

        //移除可疑方法
        vector<int>ans;
        for (int i = 0; i < n; i++)
        {
            if (sus[i] == 0)
            {
                ans.push_back(i);
            }
        }
        return ans;
    }
};

std::iota用于生成一个连续的数值序列，需要引入numeric库。

cpp 复制代码

template <class ForwardIterator, class T>
void iota(ForwardIterator first, ForwardIterator last, T value);

从T开始赋值。

377. 组合总和 Ⅳ - 力扣（LeetCode）

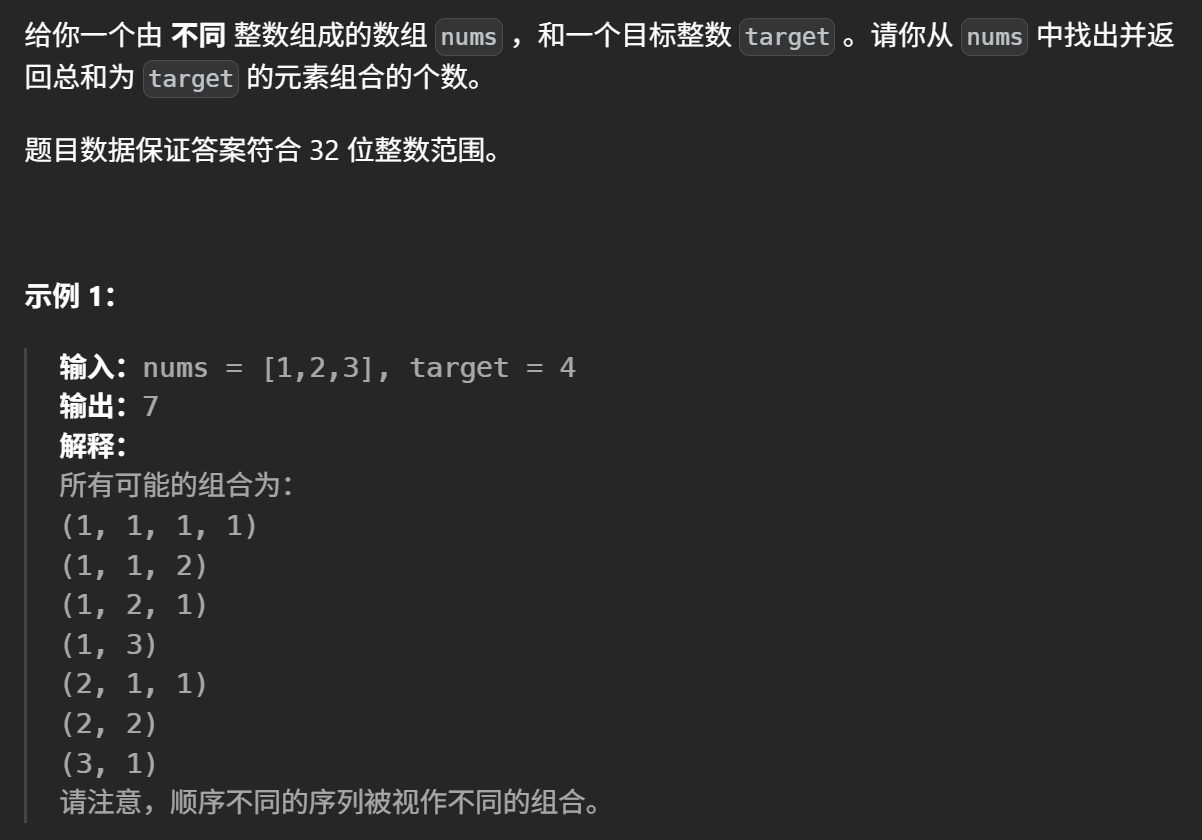
本质和爬楼梯：70. 爬楼梯 - 力扣（LeetCode）是一样的。只不过，爬楼梯的数组是 $1,2$ ，即你一次只能爬1或2个台阶。本题nums中元素表示一次能爬的台阶数。在求dp $i$ 时，遍历nums数组，假设我们遍历到了j，那么dp $i$ 加上dp $i-j$ 即可。即到达第i个阶梯有dp $i$ 个方法，现在发现还能一次走j个台阶，所以新增方法数等于到达第i-j个台阶的方法数。

cpp 复制代码

class Solution 
{
public:
    int combinationSum4(vector<int>& nums, int target) 
    {
        int n=nums.size();
        vector<unsigned>dp(target+1);
        dp[0]=1;
        for(int i=1;i<=target;i++)
        {
            for(int x:nums)
            {
                if(x<=i) dp[i]+=dp[i-x];
            }
        }
        return dp[target];
    }
};

unsigned避免数据溢出。