1、推荐文章
1、一文看懂SVM算法
2、图解机器学习|支持向量机模型详解
3、支持向量机的直观理解
2、分类问题
假设你的大学开设了一门机器学习(ML)课程。课程导师发现数学或统计学好的学生表现最佳。随着时间的推移,积累了一些数据,包括参加课程的学生的数学成绩和统计学成绩,以及在ML课程上的表现(使用两个标签描述,"优"、"差")。
现在,课程导师想要判定数学、统计学分数和ML课程表现之间的关系。也许,基于这一发现,可以指定参加课程的前提条件。
这一问题如何求解?让我们从表示已有数据开始。我们可以绘制一张二维图形,其中一根轴表示数学成绩,另一根表示统计学成绩。这样每个学生就成了图上的一个点。
点的颜色------绿或红------表示学生在ML课程上的词表现:"优"或"差"。
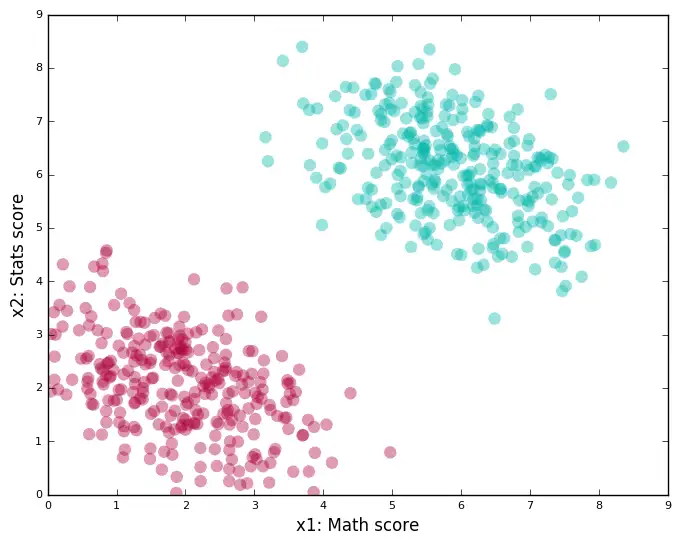
当一名学生申请加入课程时,会被要求提供数学成绩和统计学成绩。基于现有的数据,可以对学生在ML课程上的表现进行有根据的猜测。
基本上我们想要的是某种"算法",接受"评分元组"(math_score, stats_score)输入,预测学生在图中是红点还是绿点(绿/红也称为分类 或标签 )。当然,这一算法某种程度上包括了已有数据中的模式,已有数据也称为训练数据。
在这个例子中,找到一条红聚类和绿聚类之间的直线,然后判断成绩元组位于线的哪一边,是一个好算法。

这里的直线是我们的分界(separating boundary) (因为它分离了标签)或者**分类器(classifier)**(我们使用它分类数据点)。上图显示了两种可能的分类器。
好 vs 差的分类器
这里有一个有趣的问题:上面的两条线都分开了红色聚类和绿色聚类。是否有很好的理由选择一条,不选择另一条呢?
别忘了,分类器的价值不在于它多么擅长分离训练数据。我们最终想要用它分类未见数据点(称为**测试数据)。因此,我们想要选择一条捕捉了训练集中的通用模式(general pattern)**的线,这样的线在测试集上表现出色的几率很大。
上面的第一条线看起来有点"歪斜"。下半部分看起来太接近红聚类,而上半部分则过于接近绿聚类。是的,它完美地分割了训练数据,但是如果它看到略微远离其聚类的测试数据点,它很有可能会弄错标签。
第二条线没有这个问题。
我们来看一个例子。下图中两个方形的测试数据点,两条线分配了不同的标签。显然,第二条线的分类更合理。
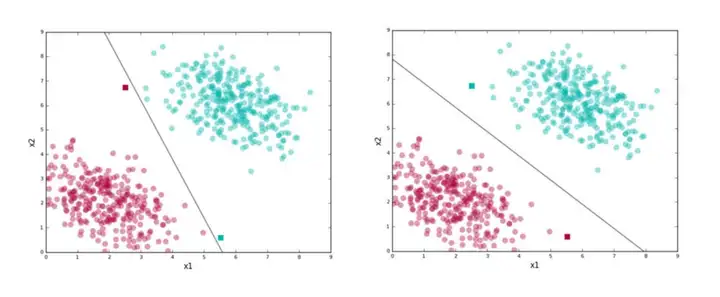
第二条线在正确分割训练数据的前提下,尽可能地同时远离两个聚类。保持在两个聚类的正中间,让第二条线的"风险"更小,为每个分类的数据分布留出了一些摇动的空间,因而能在测试集上取得更好的概括性。
SVM试图找到第二条线。上面我们通过可视化方法挑选了更好的分类器,但我们需要更准确一点地定义其中的理念,以便在一般情形下加以应用。下面是一个简化版本的SVM:
- 找到正确分类训练数据的一组直线。
- 在找到的所有直线中,选择那条离最接近的数据点距离最远的直线。
距离最接近的数据点称为支持向量(support vector) 。支持向量定义的沿着分隔线的区域称为间隔(margin)。
下图显示了之前的第二条线,以及相应的支持向量(黑边数据点)和间隔(阴影区域)。
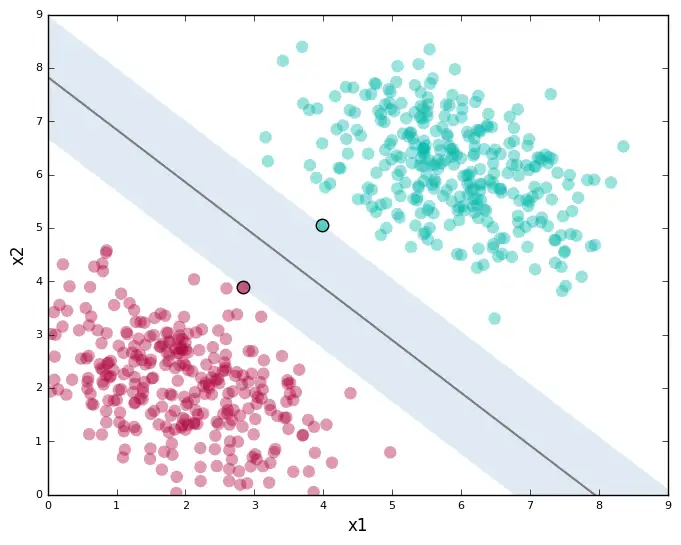
尽管上图显示的是直线和二维数据,SVM实际上适用于任何维度;在不同维度下,SVM寻找类似二维直线的东西。
例如,在三维情形下,SVM寻找一个平面(plane) ,而在更高维度下,SVM寻找一个超平面(hyperplane) ------二维直线和三维平面在任意维度上的推广。这也正是支持向量得名的由来。在高维下,数据点是多维向量,间隔的边界也是超平面。支持向量位于间隔的边缘,"支撑"起间隔边界超平面。
可以被一条直线(更一般的,一个超平面)分割的数据称为**线性可分(linearly separable)数据。超平面起到线性分类器(linear classifier)**的作用。
允许误差
在上一节中,我们查看的是简单的情形,完美的线性可分数据。然而,现实世界通常是乱糟糟的。你几乎总是会碰到一些线性分类器无法正确分类的实例。
下图就是一个例子。
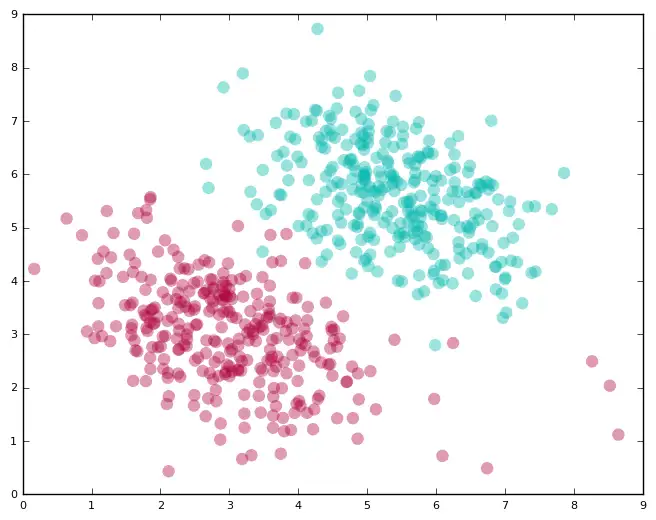
显然,如果我们使用一个线性分类器,我们将永远不能完美地分割数据点。我们同样不想干脆抛弃线性分类器,因为除了一些出轨数据点,线性分类器确实看起来很适合这个问题。
SVM允许我们通过参数C指定愿意接受多少误差。C让我们可以指定以下两者的折衷:
- 较宽的间隔。
- 正确分类训练数据 。C值较高,意味着训练数据上容许的误差较少。
再重复一下,这是一个折衷 。以间隔的宽度为代价得到训练数据上更好的分类。
下图展示了随着C值的增加,分类器和间隔的变化(图中没有画出支持向量):
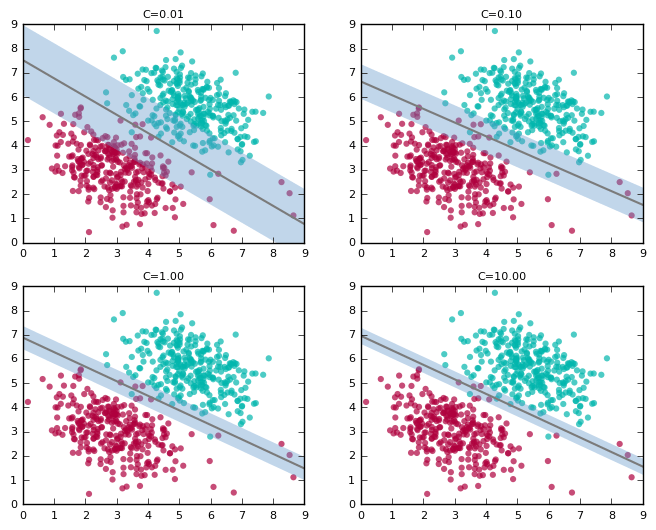
上图中,随着C值的增加,分割线逐渐"翘起"。在高C值下,分割线试图容纳右下角大部分的红点。这大概不是我们想要的结果。而C=0.01的图像看起来更好的捕捉了一般的趋势,尽管和高C值情形相比,他在训练数据上的精确度较低。
同时,别忘了这是折衷,注意间隔是如何随着C值的增加而收窄的。
在上一节的例子中,间隔曾经是数据点的"无人区"。正如我们所见,这里再也无法同时 得到良好的分割边界和相应的不包含数据点的间隔。总有一些数据点蔓延到了间隔地带。
由于现实世界的数据几乎从来都不是整洁的,因此决定较优的C值很重要。我们通常使用**交叉验证(cross-validation)**之类的技术选定较优的C值。
非线性可分数据
我们已经看到,支持向量机有条不紊地处理完美线性可分或基本上线性可分的数据。但是,如果数据完全线性不可分,SVM的表现如何呢?毕竟,很多现实世界数据是线性不可分的。当然,寻找超平面没法奏效了。这看起来可不妙,因为SVM很擅长找超平面。
下面是一个非线性可分数据的例子(这是知名的XOR数据集的一个变体),其中的斜线是SVM找到的线性分类器:
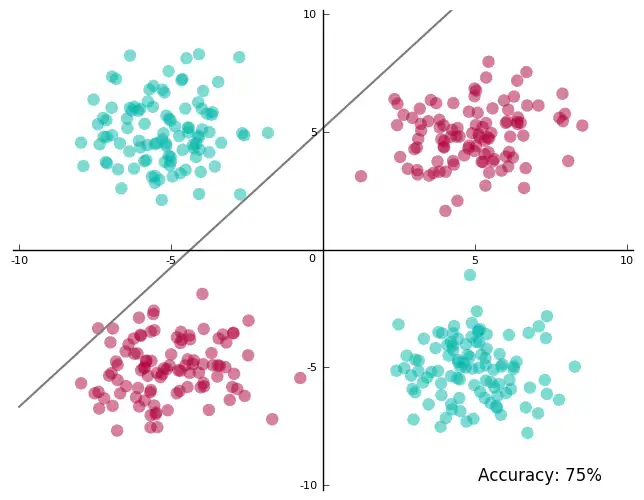
显然这结果不能让人满意。我们需要做得更好。
注意,关键的地方来了!我们已经有了一项非常擅长寻找超平面的技术,但是我们的数据却是非线性可分的。所以我们该怎么办?将数据投影到一个线性可分的空间,然后在那个空间寻找超平面!
下面我们将逐步讲解这一想法。
我们将上图中的数据投影到一个三维空间:
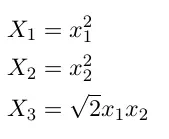
下面是投影到三维空间的数据。你是不是看到了一个可以悄悄放入一个平面的地方?

让我们在其上运行SVM:
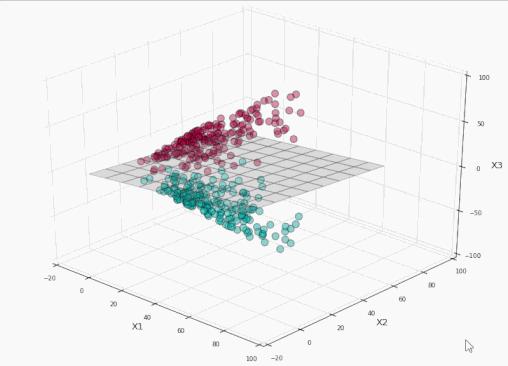
太棒了!我们完美地分割了标签!现在让我们将这个平面投影到原本的二维空间:
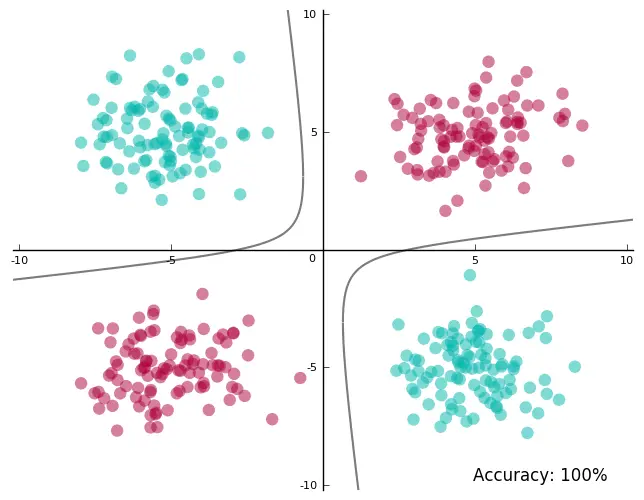
训练集上精确度100%,同时没有过于接近数据!耶!
原空间的分割边界的形状由投影决定。在投影空间中,分割边界总是一个超平面。
别忘了,投影数据的主要目标是为了利用SVM寻找超平面的强大能力。
映射回原始空间后,分割边界不再是线性的了。不过,我们关于线性分割、间隔、支持向量的直觉在投影空间仍然成立。
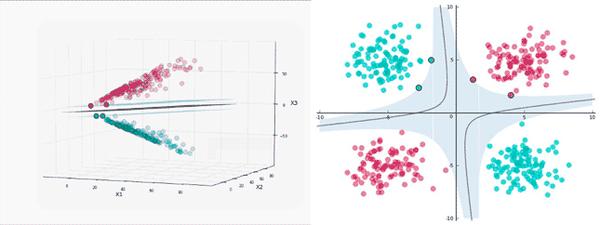
我们可以看到,在左侧的投影空间中,三维的间隔是超平面之上的平面和之下的平面中间的区域(为了避免影响视觉效果,没有加上阴影),总共有4个支持向量,分别位于标识间隔的上平面和下平面。
而在右侧的原始空间中,分割边界和间隔都不再是线性的了。支持向量仍然在间隔的边缘,但单从原始空间的二维情形来看,支持向量好像缺了几个。