14.红黑树
1.定义:
红黑树是一种自平衡的二叉查找树,是一种高效的查找树。它是由 Rudolf Bayer 于1978年发明,在当时被称为平衡二叉 B 树(symmetric binary B-trees)。后来,在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的红黑树。红黑树具有良好的效率,它可在 O(logN) 时间内完成查找、增加、删除等操作。
红黑树具备了某些特性的二叉搜索树,能解决非平衡树问题,红黑树是一种接近平衡的二叉树(说它是接近平衡因为它并没有像AVL树的平衡因子的概念,它只是靠着满足红黑节点的5条性质来维持一种接近平衡的结构,进而提升整体的性能,并没有严格的卡定某个平衡因子来维持绝对平衡)
2.特性
在讲解红黑树性质之前,先简单了解一下几个概念:
- parent:父节点
- sibling:兄弟节点
- uncle:叔父节点( parent 的兄弟节点)
- grand:祖父节点( parent 的父节点)
红黑树同时满足以下特性:
- 节点不是黑色,就是红色(非黑即红)
- 根节点为黑色
- 叶节点为黑色(叶节点是指末梢的空节点 Nil或Null)
- 一个节点为红色,则其两个子节点必须是黑色的(根到叶子的所有路径,不可能存在两个连续的红色节点)
- 每个节点到叶子节点的所有路径,都包含相同数目的黑色节点(相同的黑色高度)
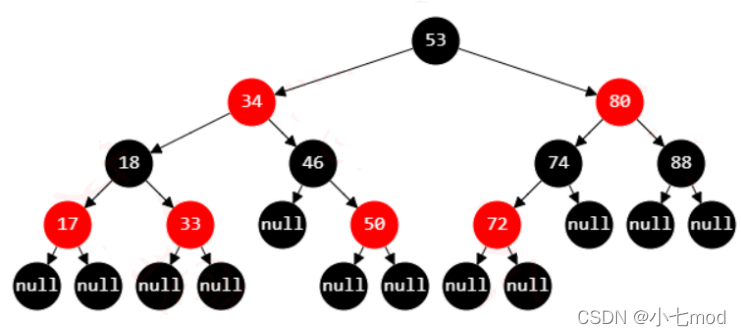
- 约束4和5,保证了红黑树的大致平衡:根到叶子的所有路径中,最长路径不会超过最短路径的2倍。
- 使得红黑树在最坏的情况下,也能有O(log2N)的查找效率
- 黑色高度为3时,最短路径:黑色→ \rightarrow→ 黑色 → \rightarrow→ 黑色,最长路径:黑色→ \rightarrow→ 红色 → \rightarrow→ 黑色 → \rightarrow→ 红色 → \rightarrow→ 黑色
- 最短路径的长度为2(不算Nil的叶子节点),最长路径为4
- 关于叶子节点:Java实现中,null代表空节点,无法看到黑色的空节点,反而能看到传统的红色叶子节点
- 默认新插入的节点为红色:因为父节点为黑色的概率较大,插入新节点为红色,可以避免颜色冲突
3.红黑树的效率
红黑树的查找,插入和删除操作,时间复杂度都是O(logN)
4.红黑树和AVL树的比较
- AVL树的时间复杂度虽然优于红黑树,但是对于现在的计算机,cpu太快,可以忽略性能差异
- 红黑树的插入删除比AVL树更便于控制操作
- 红黑树整体性能略优于AVL树(红黑树旋转情况少于AVL树)
5.红黑树的等价转换
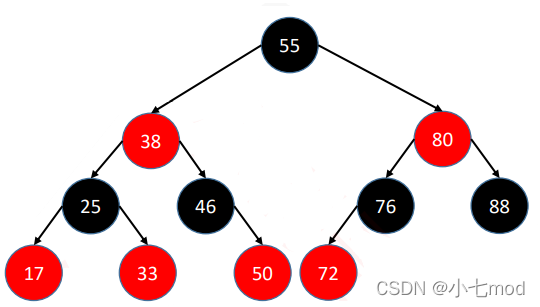
上面这颗红黑树,我们来将所有的红色节点上移到和他们的父节点同一高度上,就会形成如下结构
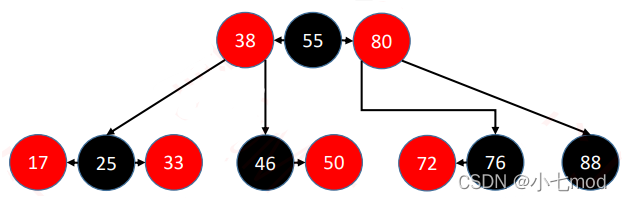
这个结构很明显,就是一棵四阶B树(一个节点最多放三个数据),如果画成如下的样子大家应该就能看的更清晰了
由上面的等价变换我们就可以得到如下结论:
- 红黑树 和 4阶B树(2-3-4树)具有等价性
- 黑色节点与它的红色子节点融合在一起,形成1个B树节点
- 红黑树的黑色节点个数 与 4阶B树的节点总个数相等
- 在所有的B树节点中,永远是黑色节点是父节点,红色节点是子节点。黑色节点在中间,红色节点在两边。
5.红黑树的左右旋转

可以理解为提着旋转另一侧的孩子节点(左旋提有孩子,右旋提左孩子),将整个树提起来
右旋节点 M 的步骤如下:
- 将节点 M 的左孩子引用指向节点 E 的右孩子
- 将节点 E 的右孩子引用指向节点 M,完成旋转
以下了解即可
6.插入
默认插入为红色节点
红黑树插入要分情况来看
1.满足红黑树的性质 4
有 4 种情况满足红黑树的性质 4 :parent 为黑色节点。这四种情况不需要做任何额外的处理。
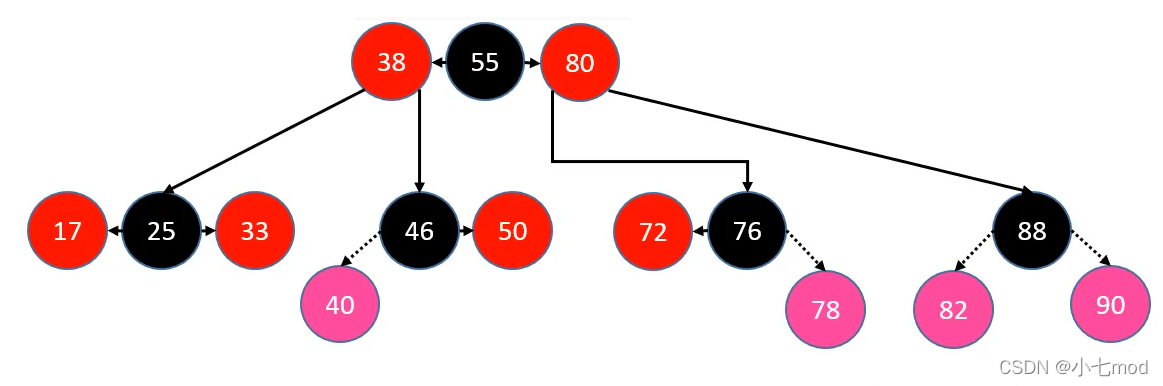
2.不满足性质4,LL RR
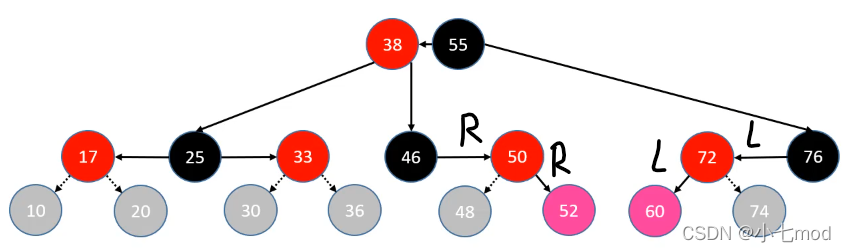
RR****情况:父节点为祖父节点的右节点,插入节点为父节点的右节点
LL情况:父节点为祖父节点的左节点,插入节点为父节点的左节点
**判定条件:**uncle 不是红色节点。
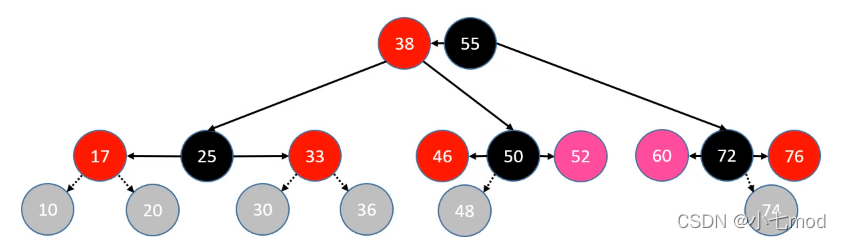
- parent 染成黑色,grand 染成红色
- grand 进行单旋操作
- LL:右旋转
- RR:左旋转
3.不满足性质4,LR RL
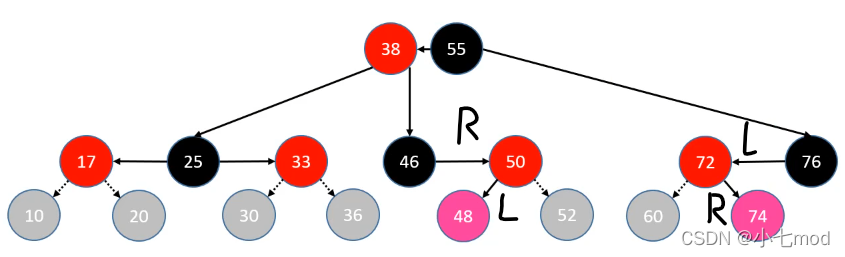
RL****情况:父节点为祖父节点的右节点,插入节点为父节点的左节点
LR情况:父节点为祖父节点的左节点,插入节点为父节点的右节点
**判定条件:**uncle 不是红色节点
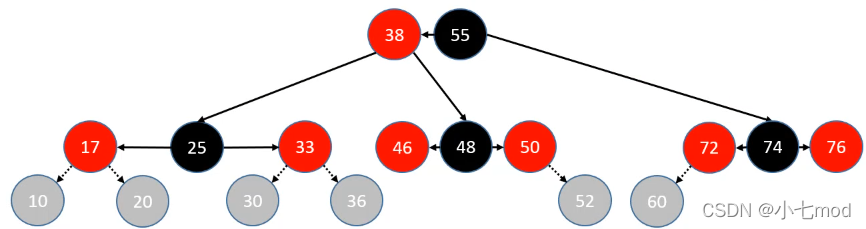
- 插入节点染成黑色,grand 染成红色
- 进行双旋操作
- LR:parent 左旋转, grand 右旋转
- RL:parent 右旋转, grand 左旋转
3.上溢的LL插入情况
超出了4阶B树节点的容量范围,这种情况称为上溢
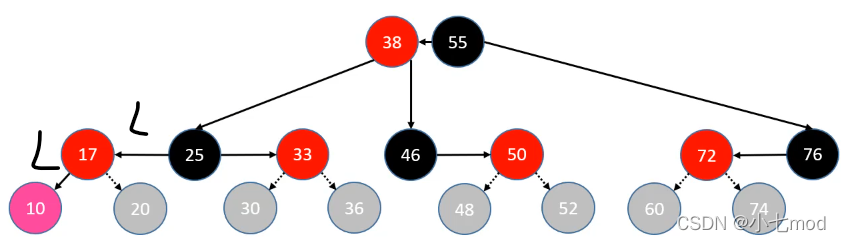
上溢LL情况:父节点为祖父节点的左节点,插入节点为父节点的左节点。并且构成的新的B树节点已经超过了B树节点容量大小范围。
**判定条件:**uncle 是红色节点。满足这个条件的就都是上溢的情况,上溢的修复只需要染色,不需要旋转。
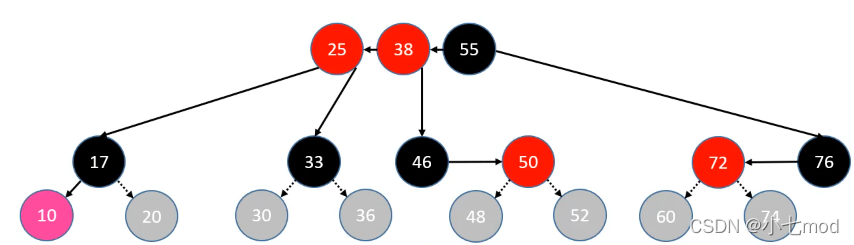
- parent、uncle 染成黑色
- grand 向上合并
- 将向上合并的grand染成红色,相对上一层,就当做是新添加的节点,再次来一遍插入情况的判断,进行处理。
4.上溢的RR插入情况
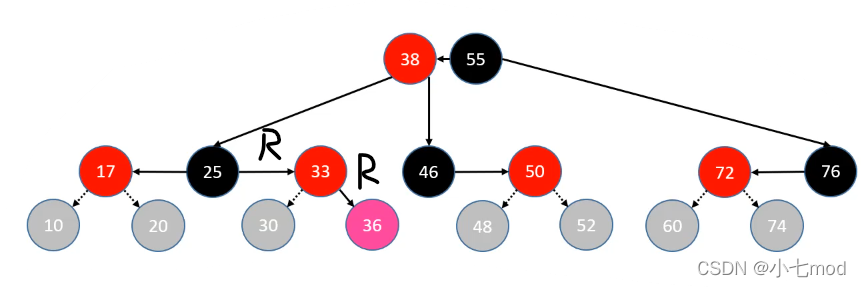
上溢RR情况:父节点为祖父节点的右节点,插入节点为父节点的右节点。并且构成的新的B树节点已经超过了B树节点容量大小范围。
**判定条件:**uncle 是红色节点
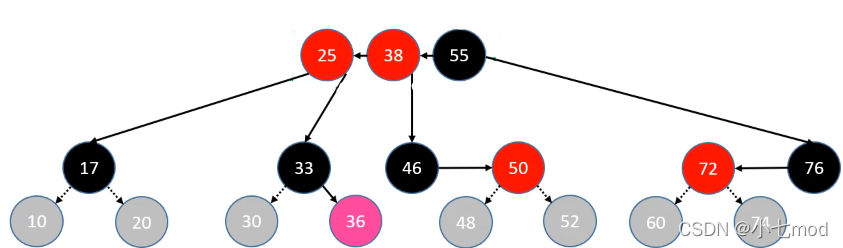
- parent、uncle 染成黑色
- grand 向上合并
- 染成红色(其实染成红色就已经是完成了向上合并,因为祖父节点和祖父节点的父节点的连接指向并没有变),当做是新添加的节点进行处理
5.上溢的LR插入情况
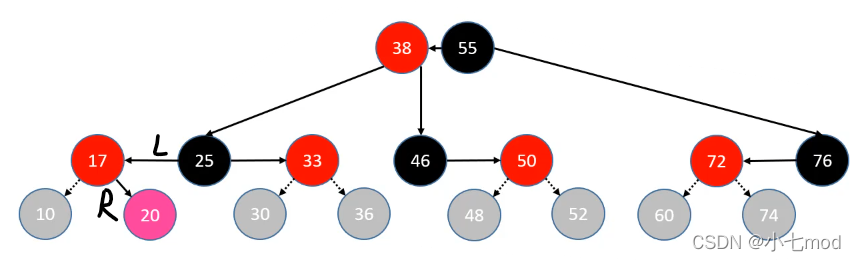
上溢LR情况:父节点为祖父节点的左节点,插入节点为父节点的右节点。并且构成的新的B树节点已经超过了B树节点容量大小范围。
**判定条件:**uncle 是红色节点
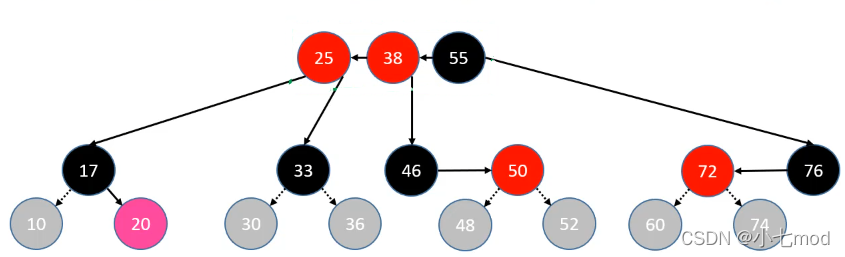
- parent、uncle 染成黑色
- grand 向上合并
- 染成红色,当做是新添加的节点进行处理
6.上溢的RL插入情况
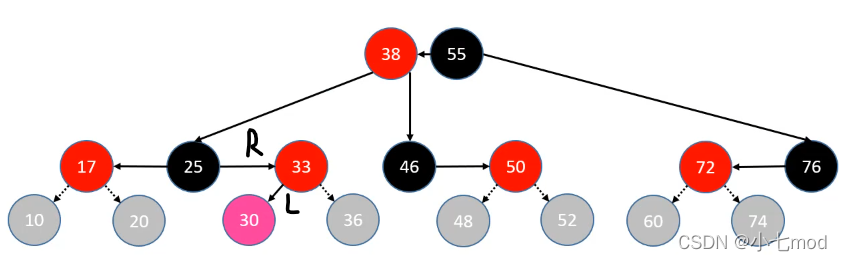
上溢RL情况:父节点为祖父节点的右节点,插入节点为父节点的左节点。并且构成的新的B树节点已经超过了B树节点容量大小范围。
**判定条件:**uncle 是红色节点
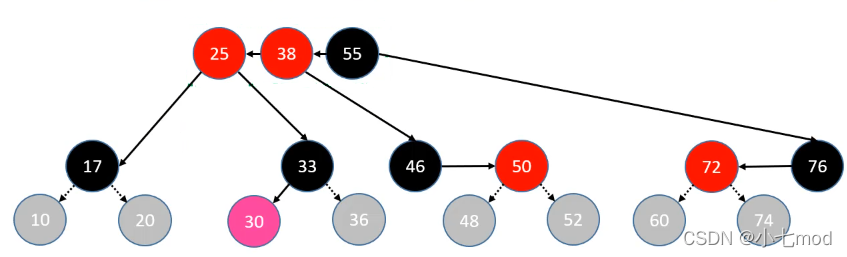
- parent、uncle 染成黑色
- grand 向上合并
- 染成黑色,当做是新添加的节点进行处理
7.删除
B树中,最后真正被删除的元素都在叶子节点中。所以在红黑树中,被删除的节点一定也在最后一层。
1.删除红色节点
直接删
2.删除拥有1个红色子节点的黑色节点
删除拥有1个红色子节点的黑色节点的情况,是需要我们做相关的处理的。
对于一个二叉树来说,删除一个度为1的节点(度指的是一个节点的子节点个数),将其删除后需要用它唯一的子节点来进行替换。而红黑树的这种情况的判定条件,就是判定要替代删除节点的子节点是不是红色
判定条件:用以替代的子节点是红色节点
修复方法:
- 用删除节点的唯一子节点对其进行替代
- 将替代节点染成黑色
3.删除黑色叶子节点------删除节点为根节点
一棵红黑树只有一个黑色根节点(也就是唯一的一个叶子节点,整个红黑树只有这一个黑色节点),可直接删除该节点,无需做其他操作。
4.删除黑色叶子节点------删除节点的兄弟节点为黑色
因为四阶B树的节点中最少存有1个元素,如果不足,则会造成下溢。也就是需要从兄弟节点中借一个子节点出来。
1.兄弟节点至少有1个红色子节点

黑色叶子节点被删除后,会导致B树节点下溢(比如删除88),就可以从兄弟节点中借出一个红色子节点来进行修复。
**判定条件:**兄弟节点至少有 1 个红色子节点
修复方法:
- 进行旋转操作
- 旋转之后的中心节点继承父节点(删除节点的父节点)的颜色
- 旋转之后的左右节点染为黑色
2.兄弟节点没有红色子节点
当删除节点的兄弟节点没有红色节点可以借出的情况下,就需要父节点来向下合并进行修复,父节点向下和兄弟节点合并成新的B树节点来解决下溢。
**判定条件:**兄弟节点没有1个红色子节点
修复步骤总结:
- 父节点向下与兄弟节点进行合并
- 将兄弟染成红色、父节点染成黑色即可修复红黑树性质
- 如果父节点是黑色,直接将父节点当成被删除的节点处理,来修复父节点的下溢情况
5. 删除黑色叶子节点------删除节点的兄弟节点为红色
删除节点的兄弟节点为红色,这样删除节点出现下溢后没办法通过兄弟节点来进行修复。这就需要先把红黑树转换为兄弟节点为黑色的情况,就可以套用上面讲的修复方法来进行修复了。
修复步骤总结:
- 兄弟节点染成 BLACK,父节点染成染成 RED,对父节点进行右旋
- 于是又回到兄弟节点是黑色的情况(侄子节点变为兄弟节点),继续使用兄弟节点为黑色的方法进行修复