序言
在深度学习领域,自编码器作为一种无监督学习技术,凭借其强大的特征表示能力,在数据压缩、去噪、异常检测及生成模型等多个方面展现出独特魅力。其中,随机编码器和解码器作为自编码器的一种创新形式,进一步拓宽了其应用边界。随机编码器通过引入随机性,如噪声注入或概率性映射,使得编码过程不再拘泥于固定的转换规则,而是能够捕捉数据中的潜在随机性和多样性。这一特性对于处理复杂多变的现实世界数据尤为关键,因为它允许模型在编码时保留更多的不确定性信息,为后续处理或生成任务提供丰富的素材。
随机编码器和解码器(Stochastic Encoders and Decoders)
-
自编码器仅仅是一个前馈网络,可以使用与传统前馈网络相同的损失函数和输出单元。
-
如
深度网络现代实践 - 深度前馈网络之基于梯度的学习篇 - 其他的输出类型中描述,设计前馈网络的输出单元和损失函数普遍策略是定义一个输出分布 p ( y ∣ x ) p(\boldsymbol{y}\mid\boldsymbol{x}) p(y∣x) 并最小化负对数似然 − log p ( y ∣ x ) -\log p(\boldsymbol{y}\mid\boldsymbol{x}) −logp(y∣x)。在这种情况下, y \boldsymbol{y} y 是关于目标的向量(如类标)。 -
在自编码器中, x \boldsymbol{x} x 既是输入也是目标。
- 然而,我们仍然可以使用与之前相同的架构。
- 给定一个隐藏编码 h \boldsymbol{h} h,我们可以认为解码器提供了一个条件分布 p model ( x ∣ h ) p_{\text{model}}(\boldsymbol{x}\mid\boldsymbol{h}) pmodel(x∣h)。
- 接着我们根据最小化 − log p decoder ( x ∣ h ) -\log p_{\text{decoder}}(\boldsymbol{x}\mid\boldsymbol{h}) −logpdecoder(x∣h) 来训练自编码器。
- 损失函数的具体形式视 p decoder p_{\text{decoder}} pdecoder 的形式而定。
- 就传统的前馈网络来说,我们通常使用线性输出单元参数化高斯分布的均值(如果 x \boldsymbol{x} x 是实的)。
- 在这种情况下,负对数似然对应均方误差准则。
- 类似地,二值 x \boldsymbol{x} x 对应参数由 sigmoid \text{sigmoid} sigmoid单元确定的Bernoulli 分布,离散的 x \boldsymbol{x} x 对应 softmax \text{softmax} softmax分布等等。
- 为了便于计算概率分布,我们通常认为输出变量与给定 h \boldsymbol{h} h 是条件独立的,但一些技术(如混合密度输出)可以解决输出相关的建模。
-
为了更彻底地区别之前看到的前馈网络,我们也可以将编码函数 ( encoding function \text{encoding function} encoding function) f ( x ) f(x) f(x) 的概念推广为编码分布 ( encoding distribution \text{encoding distribution} encoding distribution) p encoder ( h ∣ x ) p_{\text{encoder}}(\boldsymbol{h}\mid\boldsymbol{x}) pencoder(h∣x),如
图例1中所示。- 以及一个随机解码器:
p decoder ( x ∣ h ) = p model ( x ∣ h ) p_{\text{decoder}}(\boldsymbol{x}\mid\boldsymbol{h})=p_{\text{model}}(\boldsymbol{x}\mid\boldsymbol{h}) pdecoder(x∣h)=pmodel(x∣h) --- 公式1 \quad\textbf{---\footnotesize{公式1}} ---公式1
- 以及一个随机解码器:
-
一般情况下, 编码器和解码器的分布没有必要与一个唯一的联合分布 p model ( x ∣ h ) p_{\text{model}}(\boldsymbol{x}\mid\boldsymbol{h}) pmodel(x∣h) 的条件分布相容。 Alain et al. (2015) \text{Alain et al. (2015)} Alain et al. (2015) 指出将编码器和解码器作为去噪自编码器训练,能使它们渐近地相容(有足够的容量和样本)。
- 图例1:随机自编码器的结构,其中编码器和解码器包括一些噪声注入,而不是简单的函数。
-
随机自编码器的结构,其中编码器和解码器包括一些噪声注入,而不是简单的函数。
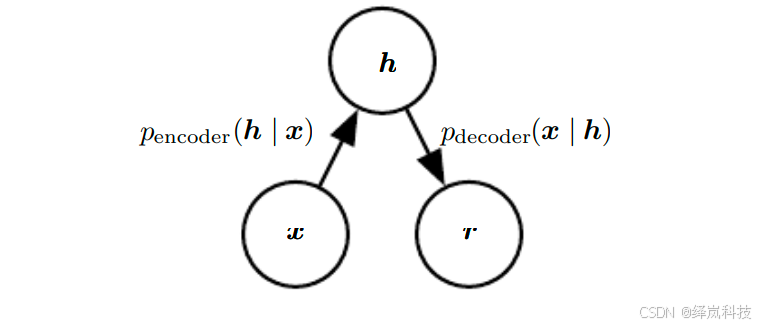
-
说明:
- 这意味着可以将它们的输出视为来自分布的采样(对于编码器是 p encoder ( h ∣ x ) p_{\text{encoder}}(\boldsymbol{h}\mid\boldsymbol{x}) pencoder(h∣x),对于解码器是 p decoder ( x ∣ h ) p_{\text{decoder}}(\boldsymbol{x}\mid\boldsymbol{h}) pdecoder(x∣h)。
-
总结
- 随机编码器和解码器的引入,为深度学习自编码器家族增添了新的活力与可能性。它们不仅增强了自编码器处理复杂数据的能力,还促进了生成模型的发展,使得生成的数据样本更加自然、多样。通过随机性的巧妙运用,这些模型能够在保持数据主要特征的同时,有效模拟真实世界中的不确定性,为图像生成、文本创作乃至更广泛的AI创作领域开辟了新路径。
- 未来,随着技术的不断进步和算法的优化,随机自编码器有望在更多领域展现其独特价值,推动人工智能技术的持续创新与发展。
往期内容回顾
深度学习自编码器 - 引言篇
深度学习自编码器 - 欠完备自编码器篇
深度学习自编码器 - 正则自编码器篇
深度网络现代实践 - 深度前馈网络之基于梯度的学习篇