第十九次CCF计算机软件能力认证-1246(过64%的代码-个人题解)

1 , 2 , 4 , 6 1,2,4,6 1,2,4,6 这四个数字有一个神奇的性质：如果将其分别取以 2 2 2 为底的幂，得到的分别是 2 , 4 , 16 , 64 2,4,16,64 2,4,16,64，仍是由这四个数字组成的。

我们从数字串 1 1 1 开始，每秒钟它的每一位都会独立地变成 2 2 2 的幂。

例如，在前几秒钟，数字串会依次变成:

css 复制代码

1.2
2.4
3.16
4.264
5.46416
6.166416264
7.264641626446416
8.46416641626446416166416264
9.166416264641626446416166416264264641626446416

显然，这些数字串都仅包含 1 , 2 , 4 , 6 1,2,4,6 1,2,4,6 这四个数字。

输入整数 n n n 和数字串 S S S，请你求出 S S S 在第 n n n 秒钟的数字串共出现了几次?

由于答案可能很大，只需要你输出它对 998244353 998244353 998244353 取模的结果。

输入格式

包含两行，第一行为一个数 n n n，第二行为一个串 S S S。

输出格式

仅有一行，含有一个整数，表示所求的答案。

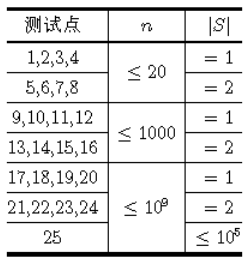
数据范围

对于所有的数据，保证要输出的答案不为 0 0 0，保证 0 ≤ n ≤ 1 0 9 0≤n≤10^9 0≤n≤109， 1 ≤ ∣ S ∣ ≤ 1 0 5 1≤|S|≤10^5 1≤∣S∣≤105。

输入样例1：

9
26

输出样例1：

样例1解释

第 9 9 9 秒的数字串为 166416264641626446416166416264264641626446416，其中出现了 5 5 5 次 26。

输入样例2：

2020
16

输出样例2：

292008622

代码写的很详细了：

我在这里简单提一下|S| = 2 ,的时候的递推表达式

其实很简单，任何一个二位数一定是有上一次的某个二位数推出来的

比如在 n = 9 的时候里面有一个26

那么，

2^2 = 4

2^6 = 64

连起来就是46 4

就相当于26 能够生成一个46，其余的只有1，2，4，6组成的二位十分有限，依次递推就可以了。

现在在 n <= 1000 的都可以做了：
已经得到64分了winning!!!

python 复制代码

n = int(input())
m = input()
mod = 998244353
target = "2"
def pwd(a , b ):
    ans = 1
    while b:
        if(b&1): ans *= a
        a *= a
        b>>=1
    return ans
    

# X =  ["1","2","4","6"]
# Y =  ["16","26","46","66","64","41","62"]
    #  2   4   16  64


def find(target , m):
    cnt  =  0 
    for i in range(len(target)-len(m)+1):
        f = True
        for j in range(len(m)):
            if target[i + j] != m[j]:f = False
        if(f): cnt += 1
    return cnt
    
if(n <= 20): # 暴力先得32分
    for i in range(n-1):
        aim = ""
        for c in target:
            aim += str(pwd(2,int(c)))
        target = aim
    print(find(target,m))
elif n <= 1000:# n > 20 , sloely 考虑 n < 1000 and |S| = 1 已经可以得到48分了
    dp = [[0] * 101 for _ in range(1001)]
    dp[1][2] = 1
    for i in range(2,n+1):
        dp[i][1] = dp[i-1][4] % mod
        dp[i][2] = dp[i-1][1] % mod
        dp[i][6] = (dp[i-1][6] + dp[i-1][4])%mod
        dp[i][4] = (dp[i-1][2] + dp[i-1][6])%mod
        # 在考虑一下|S| = 2的情况 ， 现在可以得到64分了！WIN!
        dp[i][16] = dp[i-1][4] % mod
        dp[i][64] = (dp[i-1][6] +dp[i-1][42])% mod
        dp[i][26] = dp[i-1][16] % mod
        dp[i][46] = (dp[i-1][26] + dp[i-1][66])%mod
        dp[i][66] = dp[i-1][46] % mod
        dp[i][41] = dp[i-1][64] % mod
        dp[i][62] = dp[i-1][41] % mod
        dp[i][44] = dp[i-1][62] % mod
        dp[i][61] = dp[i-1][44] % mod
        dp[i][42] = dp[i-1][61] % mod
    print(dp[n][int(m)]%mod)