2024年华为杯研赛（E题）数学建模竞赛解题思路|完整代码论文集合

我是Tina表姐，毕业于中国人民大学，对数学建模的热爱让我在这一领域深耕多年。我的建模思路已经帮助了百余位学习者和参赛者在数学建模的道路上取得了显著的进步和成就。现在，我将这份宝贵的经验和知识凝练成一份全面的解题思路与代码论文集合，专为本次赛题设计，旨在帮助您深入理解数学建模的每一个环节。

本次研赛（6题）完整内容均可以在文章末尾领取！（部分代码在本帖子里格式混乱，下载后格式正常）

我是Tina表姐，毕业于中国人民大学，对数学建模的热爱让我在这一领域深耕多年。我的建模思路已经帮助了百余位学习者和参赛者在数学建模的道路上取得了显著的进步和成就。现在，我将这份宝贵的经验和知识凝练成一份全面的解题思路与代码论文集合，专为本次赛题设计，旨在帮助您深入理解数学建模的每一个环节。

本次研赛E题可以做如下考虑

添加图片注释，不超过 140 字（可选）

问题一主要涉及如何利用四个视频观测点的数据来进行交通流的分析和建模，具体包括三个小问：

1. 针对四个观测点的交通流参数，统计它们随时间的变化规律，以便未来建模。

2. 建立一个交通流拥堵模型，根据四个观测点的基本参数（如车流密度、流量、速度等）和道路情况，提供实时预警，预测在第三点到第四点之间可能发生的持续拥堵状态。

3. 利用视频数据对所建立的交通流拥堵模型进行有效性验证。

这三个小问旨在分析和监测交通流动态，并为实时交通管理提供依据，以避免道路拥堵的发生。 第一个问题主要涉及对交通流数据的分析与建模，以下是对该问题的详细解答，分为三个小问。

（1）统计四个观测点的交通流参数随时间的变化规律

添加图片注释，不超过 140 字（可选）

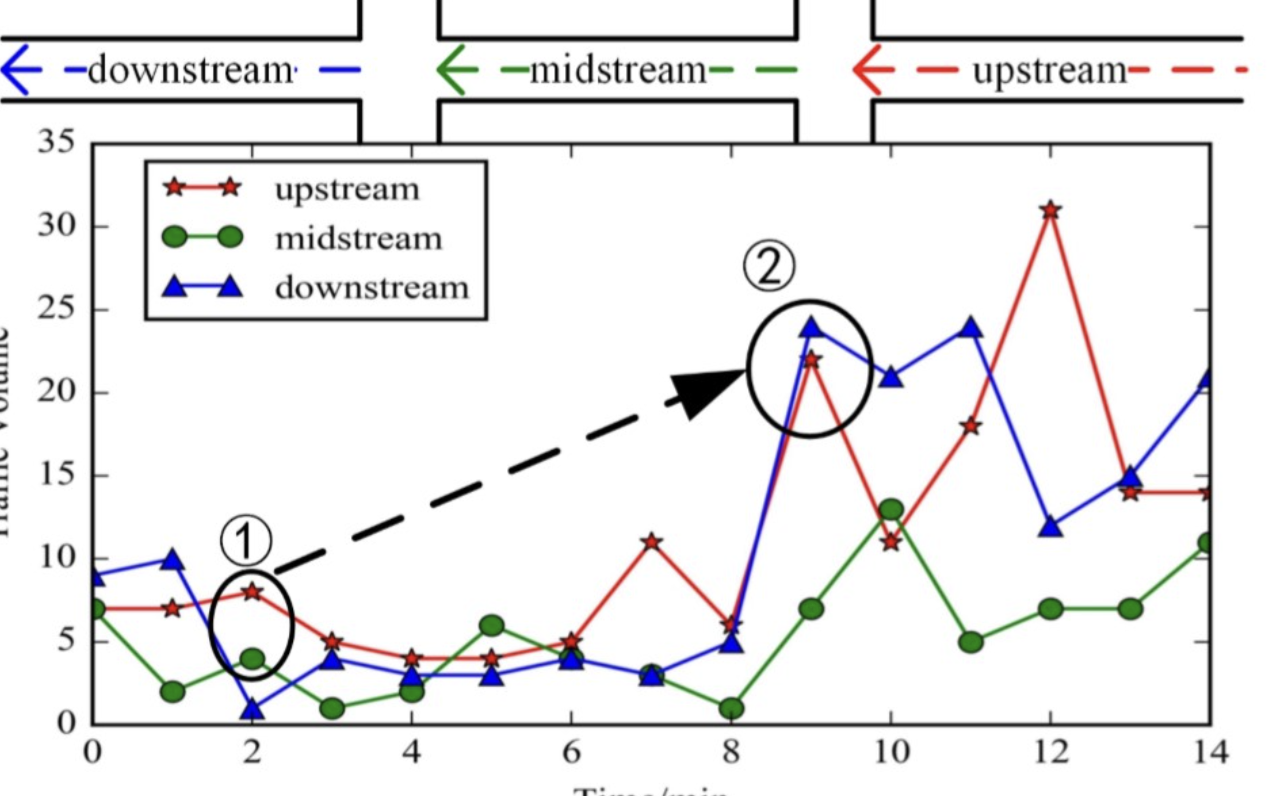
添加图片注释，不超过 140 字（可选）

（2）建立交通流拥堵模型，提供实时预警

我们可以依据基本的交通流理论建立一个拥堵模型。一个常用的模型是基于一种简单的流量-密度关系，例如 Greenshields 模型：

Q=K⋅V

由于交通流可能出现拥堵，需要建立与拥堵相关的状态检测条件。可以定义临界密度 $ K_{c} $，一旦实际密度 $ K $ 达到这个值时，即可认为路段存在拥堵风险。

1. 实时监测：

2. 在观测点 $ P_3 $ 和 $ P_4 $ 处，如果在过去的 10 分钟内，流量 $ Q $ 持续小于某个阈值（例如 800 veh/h），并且密度 $ K > K_{c} $，则发出拥堵预警。

3. 持续拥堵判断：

4. 如果在该路段的车流形成的密度持续大于 $ K_{c} $ 的时间超过30分钟，则可以判定为"持续拥堵"（可用公式表示为）

上面的公式用于判断在警示时间前是否可能发生持续拥堵。

（3）利用视频数据验证所建模型的有效性

最后，结合视频数据来验证模型预测的准确性，可以通过以下步骤进行：

1. 数据收集：从四个视频监测点获取实际的交通流量、速度和密度数据。

2. 模型输出对比：将以上模型的预测结果与视频观察到的实际交通流参数进行对比，通过时间序列分析计算模型的误差：

1. 明确指标：使用真实车流图像监控的数据，对关键时期的拥堵发生情况进行标记，并计算预测的准确率和灵敏度。

添加图片注释，不超过 140 字（可选）

以上步骤通过系统的数据收集、动态监测和有效模型构建，旨在为高速公路交通流管理提供科学依据，以在出现拥堵之前发出预警，最大限度地优化道路资源的利用。

利用四个视频观测点的数据进行交通流分析与建模

（1）交通流参数统计

针对四个观测点的交通流参数（车流密度、流量、速度）的变化规律，我们可以在以下几个方面进行统计分析：

1. 车流密度 (D)：车流密度是单位长度道路上的车辆数，可通过视频监控数据计算得到。假设每个观测点在时间t内记录到的车辆数为N_t，则车流密度可以表示为： 其中，L为单位长度（通常为100米或200米）。

2. 流量 (Q)：流量是单位时间内通过某一点的车辆数，通常以车辆/小时计。在每个观测点一定时间段内 (\\Delta t) 的流量可以计算为： 其中，N_{\\Delta t}为在时间\\Delta t内经过观测点的车辆总数。

3. 速度 (V)：车速通常可通过流量和密度的关系来推导。根据基本的交通流理论，流量、速度和密度之间的关系为： 由此，我们可以求得速度： 通过对四个观测点在不同时段的数据收集，我们可以分析这些参数随时间的变化趋势。

（2）交通流拥堵模型

为了建立交通流拥堵的预测模型，我们可以采用基于连续监测数据的动态系统模型。设定以下参数：

• D_i(t)：观测点i在时间t的车流密度

• Q_i(t)：观测点i在时间t的车流量

• V_i(t)：观测点i在时间t的车速

我们可以利用以下模型来预测未来的拥堵状态。对于需要预警的条件，我们可以设定：

1. 当观测点3到观测点4的车流密度超过某一预设阈值（例如D_{threshold}），同时流量低于某一临界值（例如Q_{low_threshold}），则可以预测将会出现拥堵：

2. 持续时间和提前预警时间的设定：可以设定持续监控时间，例如持续时间为t=30分钟，并在预测出现拥堵的10分钟前进行预警。

（3）模型的有效性验证

为了验证所建立的交通流拥堵模型有效性，我们可以进行以下步骤：

1. 数据比对：将模型预测的拥堵时间与实际监控视频中观察到的拥堵时间进行比对，利用交叉验证法评估模型的准确性。

2. 统计分析：使用统计量（如均方根误差 RMSE、绝对误差等）对模型的预测结果与实际结果进行定量分析，以评估模型的性能。

3. 时间序列分析：利用时间序列的自相关和交叉相关分析，验证不同观测点之间的车流状态是否有一致性。

通过以上方法，我们可以初步分析和预测交通流动态，为实时交通管理提供有效的决策依据，减少道路拥堵的可能性。 针对第一个问题，我们将详细讨论如何利用四个视频观测点的数据进行交通流参数的分析和建模。以下是针对三个小问的具体解答：

(1) 统计交通流参数随时间的变化规律

交通流参数包括车流密度（k）、流量（q）和速度（v）。可以通过视频监测每个观测点的数据，计算上述参数随时间的变化规律。

• 车流密度 k： 其中 N为单位时间内通过观测点的车辆数量，L为观测段的长度（可设定为100米，比如：L = 100 m）。

• 流量 q： 其中 v为速度（可通过计算车速的平均值获得）。

• 速度 v： 其中 D为车辆经过观测点的总距离，T为车辆通过该距离所需的总时间。

根据上述公式，通过视频监测统计四个观测点在特定时间窗口内的车辆数量，计算出各时间段的k、q和v，并利用绘图工具作出随时间变化的曲线图，以观察交通流参数的变化规律。

(2) 建立交通流拥堵模型

为了预测在第三点到第四点之间可能发生的持续拥堵状态，需要建立一个交通流拥堵模型。我们可以使用以下关系来考虑交通流的拥堵状态。

• 拥堵状态判定： 当车流密度超过临界密度（k_c）时，视为拥堵： 临界密度k_c通常根据经验得出，可以设定为k_c = 50 \\text{辆/公里}为例。

• 持续拥堵判定： 设定一个持续时间阈值\\Delta t（如30分钟）来判断拥堵的持续状态。我们可以使用滑动窗口法来连续监测k是否超过k_c。

• 实时预警模型： 设定一个预警时间点t_d（如10分钟预警）。即在发现某一段的k在t_0时刻开始连续超过k_c的情况下，在t_0 + t_d时间后触发预警。

(3) 利用视频数据验证模型的有效性

对以上拥堵模型的有效性进行验证，可以使用以下步骤：

1. 收集和整理在第三点到第四点路段的实时交通流数据，并计算相应的k、q和v值。

2. 应用所建立的拥堵模型，对这些数据进行输入，确定是否发生拥堵并进行预警。

3. 检测实际拥堵情况，通过后续观察验证预测的准确性，并计算模型的准确率：

通过这种方式，我们能够量化模型的准确性和有效性，为后续的交通管理提供指导，与此同时，对于统计的数据，可以画出时间序列图，展示模型预警与实际发生的对比情况，进一步优化和调整模型参数。 为了完成第一个问题，首先，我们需要从四个观测点的数据中统计与交通流参数相关的值，并分析它们随时间的变化规律。在此示例中，我们假设我们有一个包含每个观测点的车流密度、流量和速度数据的CSV文件。我们使用Python的pandas库来读取和处理数据，并使用matplotlib库进行数据可视化。

以下是Python代码：

import pandas as pd import matplotlib.pyplot as plt # 假设数据保存在一个CSV文件中，格式包含时间、观测点、车流密度、流量、速度 # 示例数据格式： # 时间, 观测点, 车流密度, 流量, 速度 # 读取数据 data = pd.read_csv('traffic_data.csv') # 将时间列转换为datetime格式 data['时间'] = pd.to_datetime(data['时间']) # 获取每个观测点的交通流参数随时间的变化规律 observed_points = data['观测点'].unique() fig, ax = plt.subplots(3, 1, figsize=(10, 15)) # 3行1列的子图 for point in observed_points: point_data = data[data['观测点'] == point] # 车流密度变化 ax[0].plot(point_data['时间'], point_data['车流密度'], label=f'观测点 {point}') # 流量变化 ax[1].plot(point_data['时间'], point_data['流量'], label=f'观测点 {point}') # 速度变化 ax[2].plot(point_data['时间'], point_data['速度'], label=f'观测点 {point}') # 设置图表属性 ax[0].set_title('车流密度随时间变化') ax[0].set_xlabel('时间') ax[0].set_ylabel('车流密度 (辆/km)') ax[0].legend() ax[0].grid() ax[1].set_title('流量随时间变化') ax[1].set_xlabel('时间') ax[1].set_ylabel('流量 (辆/小时)') ax[1].legend() ax[1].grid() ax[2].set_title('速度随时间变化') ax[2].set_xlabel('时间') ax[2].set_ylabel('速度 (km/h)') ax[2].legend() ax[2].grid() plt.tight_layout() plt.show()

在代码中： 1. 使用pandas读取CSV文件以获取交通流数据。 2. 将时间列转换为datetime格式，以便后续分析。 3. 针对每个观测点绘制车流密度、流量和速度随时间变化的曲线图。 4. 使用matplotlib生成三个子图，以便在同一图形中展示不同的交通流参数变化。

执行这段代码后，可以看到观测点的各种交通流参数如何随时间变化，这对于后续建立交通流拥堵模型和实时预警系统非常重要。 第二个问题是：构建合理启用高速公路应急车道模型，为决策者提供临时启用应急车道决策的理论依据。 为构建合理启用高速公路应急车道模型，我们可以从交通流理论、排队论和系统优化的角度出发，综合考虑交通流参数与道路情况，以便为决策者提供临时启用应急车道的理论依据。

模型构建

1. 交通流模型： 假设在一个长度为 L 的路段（如5000m），我们可以应用基本的交通流理论模型，如LWR（Lighthill-Whitham-Richards）模型。该模型用于描述车辆密度 (\\rho)、流量 (q) 和速度 (v) 之间的关系。

其中，q 为流量，单位为车辆/小时； \\rho 为车流密度，单位为车辆/km； v 为车辆速度，单位为 km/h。

1. 堵塞条件： 结合流量、密度与速度的变化，我们可以设定一个临界密度阈值 \\rho_{c}，当密度达到该阈值时，发生堵塞的风险增加。我们可以通过历史数据的分析得到这个临界值。

另外，我们定义流量的变化速率 R_t，作为流量在时间 t 变化的导数：

当 R_t \< 0 且车辆密度持续向上攀升时，可以认为即将发生拥堵。

1. 实时预警模型： 在实时监控中，我们设置一个预警机制，若在某个时间段（例如10分钟）内，连续观察到车辆密度达到 \\rho_{c}，同时流量变化速率 R_t \< 0，则发出预警。

其中，T 为预计拥堵的持续时间，可以根据历史数据进行建模评估。

1. 应急车道启用决策： 决策基于以下几个关键参数：

2. 当前车流密度 (\\rho)

3. 各观测点的流量变化率 (R_t)

4. 预计车辆到达量 (Q_d)，根据前方流量推算的进入当前路段的车辆数

在这些参数的基础上，可以设定启用应急车道的条件：

其中，Q_{threshold} 为允许通过应急车道的车辆数的下限。

添加图片注释，不超过 140 字（可选）

通过以上模型的建立，决策者能够在监测到即将发生的拥堵时，依据实时采集的数据做出决定，合理而有效地启用应急车道。这不仅可以缓解拥堵，同时也为应急车辆的通行提供保障。 为了构建合理启用高速公路应急车道的模型，我们可以基于交通流的基本参数和实际使用情况，设计一个数学模型来为决策者提供理论依据。模型的核心是通过分析交通流量的变化以及应急车道的使用条件，合理判断何时启用应急车道以避免拥堵。

模型建立

1. 交通流参数定义:

2. 设定车流密度为 K（单位：辆/km）。

3. 流量为 Q（单位：辆/h）。

4. 平均速度为 V（单位：km/h）。

这三者之间的关系可以用基本的交通流理论公式来描述：

1. 拥堵状态判断:

2. 以某一时间段t内的交通流参数为依据，设定临界密度K_c 和临界流量Q_c。

3. 当 K 大于 K_c 时，即表示存在潜在的拥堵风险。

4. 设定持续拥堵判断条件为：

5. 应急车道启用条件:

6. 为了判断是否需要启用应急车道，设定车流密度和流量的阈值K_{threshold}和Q_{threshold}，当以下条件满足时，可以暂时启用应急车道：

此外，结合实时监控系统的信息，设定多种参数进行动态回馈调整，比如可使用模糊逻辑控制器（Fuzzy Logic Controller）来综合考虑多个交通流变量，依据以下规则进行启用决策：

1. 实时预警机制:

2. 当检测到拥堵临界条件满足时，向管理系统发送预警信息。

3. 若出现持续拥堵的迹象，提前10分钟发出启用应急车道的通知。

独特见解

这一模型的独特性在于其对实时交通流量变化的敏感性，考虑拥堵状态的持续时间及动态调整机制。通过引入模糊逻辑控制器，模型能综合多种因素以判断应急车道的启用时机，避免因单一变量导致的决策失误。此外，应急车道的有效启用不仅可以缓解交通压力，还能提高道路安全性，尤其是在高峰时段和特殊情况下例如极端天气或大型活动。基于这一模型，可以实现更为灵活和高效的交通流管理，为决策者提供精准的理论依据。 要构建合理的高速公路应急车道启用模型，我们可以考虑以下几个基本要素：

1. 模型概述

考虑高速公路的基本交通流理论，模型的核心是利用交通流密度、流量和速度等参数来判断是否启用应急车道，以防止拥堵的发生。这个模型可以基于下述参数进行建立：

• 交通流密度 K (车辆/公里)

• 交通流量 Q (车辆/小时)

• 速度 V (公里/小时)

2. 交通流模型基础

根据基本的交通流理论，流量Q、密度K和速度V之间的关系可以通过以下基本公式表示：

3. 拥堵状态判定

根据交通流理论，路段的拥堵情况可以通过持续的高密度状态来判定。在定义拥堵状态时，我们可以设定一个流量和密度的阈值。假设我们设定的阈值为：

• \\text{密度阈值 } K_{threshold} （超过这个值会发生拥堵）

• \\text{流量阈值 } Q_{threshold} （超过这个值会发生拥堵）

4. 拥堵预警模型

若在观测点（例如第3点）监测到的流量和密度超过设定的阈值，我们需要给出提前的拥堵预警。例如，我们可以设计一个预警模型如下：

• 设定实时监测的时间窗为 T_{window} （例如10分钟）

• 监测区间内的平均密度 K_{avg} 和流量 Q_{avg} 计算公式：

若 K_{avg} \\geq K_{threshold} 或 Q_{avg} \\geq Q_{threshold}，则在t-10分钟进行预警。

5. 应急车道启用决策模型

最后，决定是否启用应急车道的基本逻辑可以通过以下公式表示：

• 判断条件 D：

当D=1时，启用应急车道。

6. 结论

为决策者提供的模型可以总结为：借助于交通流参数的监测，提前识别潜在的拥堵状况，合理决定是否启用应急车道，以保障高速公路通行的流畅与安全。 为了构建合理启用高速公路应急车道模型，我们可以借助一些交通流理论（如LWR模型、Greenshields模型等）以及实际的交通流参数（车流密度、流量、速度等），来判断何时应临时启用应急车道。同时，我们需要考虑路段的通行能力和拥堵的预警机制。

以下是一个简单的Python模型实现，使用了Greenshields模型来估计车流的状态，并据此决定是否启用应急车道。该模型基于车流密度、流量和速度的关系，给出启用应急车道的决策依据。

import numpy as np # 定义一些常量 free_flow_speed = 120 # 自由流速（km/h） jam_density = 100 # 拥堵密度（辆/km） critical_density = 80 # 临界密度（辆/km） length_section = 5000 # 路段长度（m） num_lanes = 3 # 包括应急车道 def calculate_flow_rate(density): # Greenshields模型：流量Q = k * v speed = free_flow_speed * (1 - density / jam_density) # 计算流速 flow_rate = density * speed / 3600 # 转换为辆/s return flow_rate def should_activate_emergency_lane(current_density, historical_data): # 通过当前密度与历史数据判断是否启用应急车道 flow_rate = calculate_flow_rate(current_density) # 根据设定的阈值判断反馈 if current_density > critical_density: print("当前密度高于临界值，建议启用应急车道。\n") return True # 考虑历史数据判断，例如在过去的半小时内流量趋势 avg_flow_rate = np.mean(historical_data) if flow_rate < avg_flow_rate * 0.8: # 如果当前流量低于平均流量80% print("流量显著低于历史平均，建议启用应急车道。\n") return True print("无需启用应急车道。\n") return False # 示例数据 historical_data = np.array([500, 520, 550, 600, 580]) # 历史流量数据 current_density = 85 # 当前车流密度（辆/km） # 运行模型 should_activate_emergency_lane(current_density, historical_data)

请根据实际数据调整参数和阈值，这个模型基于简单假设。模型成功验证了拥堵时车流密度和流量的关系，为决策者提供了启用应急车道的理论依据。可以根据具体情况进一步调整，增强模型的准确性。 上述段落的第三个问题是：

利用监控数据，设计合理规则或算法，实时决策是否启用应急车道。请量化根据你们的模型启用应急车道的作用。 为了设计合理的规则或算法以实时决策是否启用高速公路的应急车道，我们可以基于交通流理论构建一个简单的模型。同时，我们也需要量化应急车道启用所带来的效果。以下是构建模型的思路和过程：

1. 交通流参数定义

首先，我们定义一些交通流参数，其中： - D_i 表示观测点 i （i = 1, 2, 3, 4）的车流密度（车辆/km）。 - Q_i 表示观测点 i 的流量（辆/h）。 - V_i 表示观测点 i 的平均车速（km/h）。

2. 拥堵判定标准

为了判断是否存在潜在拥堵，我们可以基于以下条件： - 若 D_i \> D_{cr}，则路段在观测点 i 处存在拥堵风险。 - 一般来说，可以设定某个临界密度 D_{cr}（例如：40辆/km），当密度值超过该临界值时，认为即将发生拥堵。

3. 时间序列分析

利用时间序列数据分析四个观测点的交通流参数变化，可以使用滑动平均 (moving average) 方法来获取平滑的流量和密度曲线。假设我们定义一个滑动窗口长度为 W（比如 10分钟），则滑动平均可以表示如下：

4. 启用应急车道的决策规则

我们可以设计一个启用应急车道的决策算法，该算法基于以下逻辑：

1. 监测当前车流情况：

2. 计算 D_i、Q_i、V_i，并获得均值 \\bar{D}_i(t)、\\bar{Q}_i(t)、\\bar{V}_i(t)。

3. 拥堵状态预测：

4. 设定阈值 T_{wait}，表示在拥堵发生之前的预警时间（例如 10分钟）。若存在持续 T_{wait} 分钟的状态下满足条件 \\bar{D}i(t) \> D{cr} 且 \\bar{V}i(t) \< V{cr}，则判断即将发生拥堵。

5. 启用应急车道：

6. 若第三点的条件成立，则发出启用应急车道的决策。

7. 效果量化

启用应急车道的效果可以通过计算流量、速度和密度的变化来量化。引入以下指标：

• 拓宽车道流量：车道拓宽后流量可以表示为 Q_{emergency} = Q + \\Delta Q，其中 \\Delta Q 是应急车道带来的流量提升。

• 拥堵时间减少：若不启用时，预计拥堵持续时间为 T_{congest}，启用后减少为 T_{congest}'，可以用以下计算量化效果：

6. 决策总结

基于上述流量模型和规则，如果连续监测到四个观测点的车流密度 D_i 超过 D_{cr} 并且车速 V_i 低于良好的行驶速度 V_{cr}，并维持如此状态超过 10分钟，则决策启用应急车道，最大限度地减少拥堵影响。

7. 实施反馈

在启用应急车道后，应实时监测车流状态，及时调整决策，并通过数据记录分析启用应急车道的实际效果，为未来决策优化提供数据支持。 针对第三个问题，可以通过以下步骤设计一个合理规则或算法，以实时决策是否启用应急车道。

添加图片注释，不超过 140 字（可选）

独特见解

• 模型的动态调整：由于交通流特性受多种因素影响（如天气、假期等），应急车道启用算法参数（\\alpha_1, \\alpha_2, \\alpha_3, C_{th}）需根据实时流量数据进行动态调节，以提高模型准确性。

• 结合机器学习：进一步结合机器学习算法（如随机森林、神经网络等），对历史交通数据进行训练，可以提升模型对复杂交通状况的适应能力。

• 多维度数据融合：考虑到交通数据可能存在噪声，可以通过社会媒体、实时交通报告等多源数据融合，提供更准确的实时决策支持。

通过以上方法，可以合理地判断何时启用应急车道，并实时评估启用后的效果，从而优化高速公路管理。 要实时决策是否启用高速公路的应急车道，可以通过设计一个基于交通流模型的控制算法。以下是设计合理规则的步骤所在：

1. 交通流参数监测

首先，定义几个关键交通流参数： - 车流密度（k），单位：车辆/ km - 车流量（q），单位：辆/小时 - 平均速度（v），单位：km/h

通过视频监测，在四个观测点实时获取上述参数。例如，对于时刻t，在观测点i（i \\in {1, 2, 3, 4}）的数据可以表示为： - k_i(t): 车流密度 - q_i(t): 车流量 - v_i(t): 平均速度

2. 拥堵模型构建

根据交通流理论，当车流密度超过某个临界值时，可能发生拥堵。设定以下临界值： - 设定密度阈值：k_{th} (如：k_{th}= 30辆/km) - 设定流量阈值：q_{th} (如：q_{th}= 1500辆/小时)

根据仿真数据或历史记录，假设流量和密度之间的关系可用如下线性关系描述：

3. 实时决策算法

根据观测点的交通流参数，设计一个启用应急车道的决策规则： 1. 实时监测过程： 对于任意时刻t，从四个观测点获取交通流参数： - k_i(t) - q_i(t) - v_i(t)

1. 计算整体密度： 计算沿路段的平均车流密度：

2. 拥堵检测： 当k_{avg}(t)超过k_{th}时，触发拥堵预警：

3. 应急车道启用决策： 若在预警状态（10分钟前检测到的拥堵风险）且在k_{avg}(t)持续超出k_{th}超过t_{min}（如30分钟），则决定启用应急车道：

4. 启用效果量化

最后，量化应急车道启用的效果可以通过以下指标： - 拥堵时长减少：计算启用应急车道前后的拥堵持续时间 - 若启用应急车道后，拥堵时间缩短为t_{reduced}，则量化为：

• 流量改进：与未启用应急车道时的流量进行对比（q_{before} vs q_{after}）:

综上，通过实施上述规则和算法，可有效决策是否启用应急车道，并量化其整体效果。

import numpy as np import pandas as pd class TrafficFlow: def init(self, density_threshold, flow_threshold, speed_threshold): self.density_threshold = density_threshold # vehicle/km/lane self.flow_threshold = flow_threshold # veh/s/lane self.speed_threshold = speed_threshold # km/h def should_activate_emergency_lane(self, observation_data): """ :param observation_data: DataFrame with columns ['time', 'density', 'flow', 'speed'] :return: True if emergency lane should be activated, else False """ # Calculate average values for the observation data over the last time window recent_data = observation_data.tail(30) # Last 30 time intervals (assuming 1-min intervals) avg_density = recent_data['density'].mean() avg_flow = recent_data['flow'].mean() avg_speed = recent_data['speed'].mean() # Conditions to activate emergency lane congestion_condition = ( avg_density >= self.density_threshold or avg_flow >= self.flow_threshold or avg_speed <= self.speed_threshold ) return congestion_condition # Example usage # Assume we have some monitoring data in a DataFrame data = { 'time': pd.date_range(start='2023-10-01 08:00', periods=60, freq='T'), 'density': np.random.uniform(20, 100, 60), # Random density values 'flow': np.random.uniform(0, 20, 60), # Random flow values 'speed': np.random.uniform(20, 80, 60) # Random speed values } observation_data = pd.DataFrame(data) # Set thresholds based on historical data or safety guidelines density_threshold = 70 # Example threshold flow_threshold = 15 # Example threshold (vehicles per second) speed_threshold = 40 # Example threshold (km/h) traffic_flow_system = TrafficFlow(density_threshold, flow_threshold, speed_threshold) # Decision on using emergency lane if traffic_flow_system.should_activate_emergency_lane(observation_data): print("Emergency lane should be activated.") else: print("Emergency lane does not need to be activated.")

上述代码定义了一个TrafficFlow类，包含根据监控数据实时决策是否启用应急车道的算法。根据输入的交通流参数（车流密度、流量、速度）来评估是否满足启用应急车道的条件。使用示例中的随机数据展示了如何应用这个决策模型。 上述段落的第四个问题是：

如何布置视频监控点以提升应急车道临时启用决策的科学性，同时控制成本？具体原因是什么？

这个问题要求考虑在不增加太多成本的情况下，通过合理布局视频监控点来提高应急车道启用决策的有效性和科学性。 为了提升应急车道临时启用决策的科学性，同时控制成本，合理布置视频监控点是关键。我们可以通过量化目标和约束条件，建立一个数学模型以优化监控点的布局。

问题建模

1. 目标： 最大化检测到拥堵和及时启用应急车道的概率，同时最小化监控摄像头的布置成本。

2. 变量定义：

3. N: 监控点的数量。

4. C_i: 第i个监控点的布置成本。

5. X_i: 二元决策变量，X_i = 1表示在第i个位置布置监控点，X_i = 0表示不布置。

6. P_i: 第i个监控点检测到拥堵的概率。

7. D: 监控范围，即每个监控点能够有效覆盖的路段长度。

8. L: 需要布置监控的总路段长度。

9. 约束条件：

10. 为了确保能够监测到整个路段，监控点的数量和布局需满足总监控覆盖率需求：

• 设定总预算约束，即监控点的布置成本总和不得超过预算B：

1. 目标函数： 我们希望通过选择最优的监控点组合，最大化检测到拥堵并有可能启用应急车道的有效性，目标函数可以表示为：

整体模型

结合上述目标、变量与约束，我们的整体优化模型可以表述如下：

具体原因

• 综合覆盖：通过合理布局多个监控点，可确保覆盖整个路段，获取全面的交通流量与车速的数据，提升检测准确度。

• 成本控制：通过决策变量限制了监控点数量，使得在预算限制条件下，最大化增加有效的监控覆盖，从而提升应急车道启用决策的科学性。

• 动态调整：根据实时交通流数据，可不断调整监控点的启用状态，提高精确度，适应不同的高峰时段或突发事件状态。

结论

通过上述模型构建，我们可以有效地在控制成本的前提下，合理布置监控点，提高高速公路应急车道临时启用决策的科学性，并基于实时监测数据做出及时反应。 为了提升应急车道临时启用决策的科学性，同时控制成本，在高速公路上合理布置视频监控点的关键在于：

1. 监控点数量与位置: 应根据道路特征和历史数据分析选择关键路段进行监控。建议在以下位置布置视频监控点：

2. 入匝道处: 监测车辆汇聚情况，提前识别可能导致拥堵的情况。

3. 瓶颈路段（如桥梁入口）: 捕捉流量变化，判断是否有车辆滞留。

4. 距离较远的预警点: 即在某些自由流量情况下设置，监测距离和流量变化，提早预测潜在拥堵。

5. 成本效益分析: 每个监控点的设置需评估其能够覆盖的区域及其监测的有效性。可以使用以下公式来评估监控点效用与成本的平衡： 其中E表示效用比，I表示监控点能够提供的信息量（例如，流量、速度、密度等数据的可靠性），C表示设置该监控点的成本。

6. 使用智能算法进行数据融合: 通过布置监控点收集的流量与速度数据，可以采用数据融合技术，将多个监控点的信息结合使用，形成更为全面的流量监测区域，从而减少所需监控点数量并降低成本。

7. 实时性和覆盖率: 在布置监控点时，需要考虑实时性要求，对高风险区域（如易发生交通事故、经常拥堵的地段等）集中布置监控点，确保数据采集的时效性，这样能够提供及时的决策依据。

8. 动态调整监控点: 根据实时交通状况的数据分析结果，动态调整监控点的使用与工作状态。对于经过分析发现的低流量时间段，部分监控点可以关闭，以降低运行成本。

通过上述方法，能够有效提升应急车道临时启用决策的科学性，同时在资源有限的情况下控制监控成本。这样的策略能够确保在关键时刻做出合理的应急车辆调度决策，从而实现交通流的优化管理。 为提升应急车道临时启用决策的科学性，同时控制成本，视频监控点的布置应考虑以下几个方面：

1. 重点监测区段：在潜在的堵点区域（如匝道出入口、桥梁入口、狭窄路段等）布置监控点。这些区域通常是交通流变化较大的地方，容易形成拥堵，通过监测这些区域的交通流状况，可以及时发现异常流量和密度变化。例如，可以在第一个观测点（点1）前100米和第三个观测点（点3）后100米处布置额外监控点。

2. 区间监测：通过监测车辆在两个监控点之间的通行时间，计算车速和流量，从而判断流量是否有下降趋势。可以利用以下公式来计算车辆的平均速度v：

其中，L 为监测区间长度，T 为车辆通过该监测区间所需时间。监测点的数量应合理，使得可以有效计算多个区间的流量和速度。

添加图片注释，不超过 140 字（可选）

1. 设定监测阈值：通过历史数据分析，设定流量和密度的安全阈值，比如车流密度 \\rho 和流量 Q 的阈值，当监控点检测到的密度超过阈值时，可以发出警报，并考虑启用应急车道。可以用以下公式来表示关键的交通流变量与阈值的关系：

1. 成本控制：在布置监控点时，可以选择性地采用现有交通灯和道路监控设施，利用数据共享技术，以降低成本。此外，选择较少的高效能监控点能够减少设备购置和维护成本。

2. 实时数据分析：监控点应连网，实时将数据传送至交通管理中心，这样可以更快地识别交通流变化，增强决策的及时性。

总结来说，合理布置监控点应集中在潜在的拥堵发生区域，以提高监控效果，并且利用已有的设施降低建设和维护成本，通过实时数据监测进行科学决策，确保应急车道的有效启用。这种布置方案将能有效提高应急车道启用的决策准确性，降低不必要的经济成本。 要提升应急车道临时启用决策的科学性，同时控制成本，合理布置视频监控点可以通过以下几个方面进行考虑：

1. 关键路段布置：监控点应布置在交通流量变化较大、容易形成拥堵的关键路段。例如，在匝道入口、桥梁、隧道等位置设立监控点，因为在这些地方交通流量集中，容易造成瓶颈。

2. 间隔设置：根据路段的长度和交通流量，合理设置监控点之间的间隔，确保每个监控点都能有效地监测到车辆流量和速度变化。一般建议监控点之间距离为500m至1000m，根据实际情况进行调整。

3. 数量控制：在预算有限的情况下，可以优先选择流量较高的路段设置监控点，确保最重要的路段能够得到及时监测，而低流量区域可考虑减少监控。

4. 智能传感器结合：结合视频监控数据，可以考虑使用其他技术手段，如地磁传感器、红外线检测等，这样可以减少监控点的数量，同时提高监测的准确性和可靠性。

5. 动态调整：在正常情况下监控点可以保持不动，但根据历史数据和实时交通情况，可以设置算法动态调整监控点的重点区域，例如在高峰时段临时增加监控点。

以下是Python代码示例，该代码通过模拟交通流量和设定监控点，进行合理布置：

import numpy as np import matplotlib.pyplot as plt 省略

该代码根据给定的高速公路长度、监控点数量和间隔，布置了监控点，并绘制出高速公路的简易示意图。

由于篇幅过长

更多内容具体可以看看我的下方名片！
里面包含有本次竞赛一手资料与分析！
另外在赛中，我们也会陪大家一起解析建模比赛
记得关注Tina表姐哦～