【树结构与栈】中等力扣练习题

二叉树中和为目标值的路径

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。叶子节点 是指没有子节点的节点。

示例 1：

复制代码

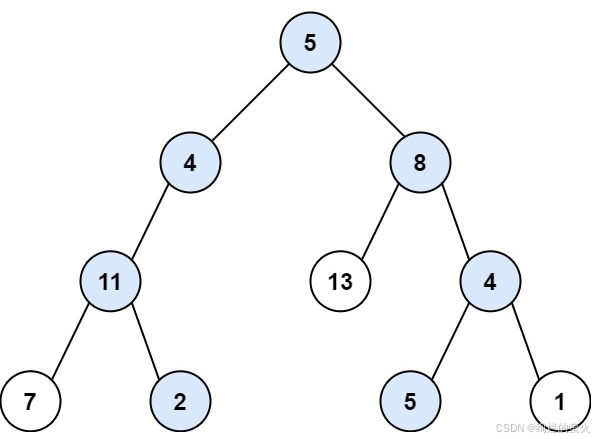
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

提示：

树中节点总数在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000

/**
- Definition for a binary tree node.
- public class TreeNode {
- ```
int val;
```
- ```
TreeNode left;
```
- ```
TreeNode right;
```
- ```
TreeNode() {}
```
- ```
TreeNode(int val) { this.val = val; }
```
- ```
TreeNode(int val, TreeNode left, TreeNode right) {
```
- ```
    this.val = val;
```
- ```
    this.left = left;
```
- ```
    this.right = right;
```
- ```
}
```
- }
  */
  class Solution {
  List<List<Integer>> ret = new LinkedList<List<Integer>>();
  //存储路径的队列
  Deque<Integer> path = new LinkedList<Integer>();
  
  public List<List<Integer>> pathSum(TreeNode root, int target) {
  //二叉树
  dfs(root, target);
  return ret;
  }
  
  public void dfs(TreeNode root, int target) {
  //根节点为空
  if (root == null) {
  return;
  }
  path.offerLast(root.val);
  target -= root.val;
  //子节点为空
  if (root.left == null && root.right == null && target == 0) {
  ret.add(new LinkedList<Integer>(path));
  }
  //遍历左子树
  dfs(root.left, target);
  //遍历右子树
  dfs(root.right, target);
  path.pollLast();
  }
  }

彩灯装饰记录I

一棵圣诞树记作根节点为 root 的二叉树，节点值为该位置装饰彩灯的颜色编号。请按照从左到右的顺序返回每一层彩灯编号。

复制代码

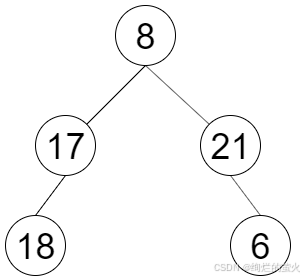
输入：root = [8,17,21,18,null,null,6]
输出：[8,17,21,18,6]

提示：

节点总数 <= 1000

/**
- Definition for a binary tree node.
- public class TreeNode {
- ```
int val;
```
- ```
TreeNode left;
```
- ```
TreeNode right;
```
- ```
TreeNode(int x) { val = x; }
```
- }
  */
  class Solution {
  ArrayList<Integer> a=new ArrayList<Integer>();
  public int[] levelOrder(TreeNode root) {
  Queue<TreeNode> q=new LinkedList<TreeNode>();
  //根节点为空
  if(root==null) return new int[0];
  //添加根节点
  q.add(root);
  //当队列中存储的节点不为空时，进行遍历
  while(!q.isEmpty()){
  TreeNode t=q.poll();
  //添加节点的数值
  a.add(t.val);
  //左边子节点不为空
  if(t.left!=null) q.add(t.left);
  //右边子节点不为空
  if(t.right!=null) q.add(t.right);
  }
  int[] re= new int[a.size()];
  //遍历查询列表中的值
  for(int i=0;i<a.size();i++){
  re[i]=a.get(i);
  }
  return re;
  }
}

验证图书取出顺序

现在图书馆有一堆图书需要放入书架，并且图书馆的书架是一种特殊的数据结构，只能按照一定的顺序放入和拿取书籍。

给定一个表示图书放入顺序的整数序列 putIn，请判断序列 takeOut 是否为按照正确的顺序拿取书籍的操作序列。你可以假设放入书架的所有书籍编号都不相同。

示例 1：

**输入：**putIn = [6,7,8,9,10,11], takeOut = [9,11,10,8,7,6]

**输出：**true

**解释：**我们可以按以下操作放入并拿取书籍： push(6), push(7), push(8), push(9), pop() -> 9, push(10), push(11),pop() -> 11,pop() -> 10, pop() -> 8, pop() -> 7, pop() -> 6

示例 2：

复制代码

输入：putIn = [6,7,8,9,10,11], takeOut = [11,9,8,10,6,7]
输出：false
解释：6 不能在 7 之前取出。

提示：

0 <= putIn.length == takeOut.length <= 1000
0 <= putIn[i], takeOut < 1000
putIn 是 takeOut 的排列。

class Solution {
public boolean validateStackSequences(int[] pushed, int[] popped) {
//创建栈
Stack<Integer> p1=new Stack<Integer>();
Stack<Integer> p2=new Stack<Integer>();
int pop=0;
for(int i=0;i<pushed.length;i++){
//插入数值
p1.push(pushed[i]);
//只要查询的栈内数值不为空，或栈顶数值与取出的数值不相符时，进行循环
while(!p1.isEmpty()&&popped[pop]==p1.peek()){
//弹出数值
p1.pop();
pop++;
}
}
//根据p1是否为空，判断取出顺序是否一致
return p1.isEmpty();
}
}