论文链接: https://arxiv.org/abs/1707.06347
补充资料: Simplified PPO-Clip Objective 推导

文章目录
- 摘要
- [1 引言](#1 引言)
- [2 背景:策略优化](#2 背景:策略优化)
-
- [2.1 策略梯度方法](#2.1 策略梯度方法)
- [2.2 信任区域方法](#2.2 信任区域方法)
- [3 裁剪的代理目标函数](#3 裁剪的代理目标函数)
- [4 自适应 KL 惩罚系数](#4 自适应 KL 惩罚系数)
- [5 算法](#5 算法)
- [6 实验](#6 实验)
-
- [6.1 代理目标 比较](#6.1 代理目标 比较)
- [6.2 连续域 与其它算法比较](#6.2 连续域 与其它算法比较)
- [6.3 连续域示例: 人形跑步和转向](#6.3 连续域示例: 人形跑步和转向)
- [6.4 在 Atari 域 与其它算法的比较](#6.4 在 Atari 域 与其它算法的比较)
- [7 结论](#7 结论)
- [8 致谢](#8 致谢)
- 参考文献
- 附录
-
- [B 雅达利Atari 游戏上的更多表现](#B 雅达利Atari 游戏上的更多表现)
摘要
We propose a new family of policy gradient methods for reinforcement learning, which alternate between sampling data through interaction with the environment, and optimizing a "surrogate" objective function using stochastic gradient ascent. 【我们提出了...用于...的方法,可以干什么?】
我们提出了一系列用于强化学习的新策略梯度方法,这些方法通过 与环境交互来交替采样数据,并使用随机梯度上升来优化"代理"目标函数。
Whereas standard policy gradient methods perform one gradient update per data sample, we propose a novel objective function that enables multiple epochs of minibatch updates. 【关键 idea】
标准的策略梯度方法 对每个数据样本执行一次梯度更新,我们提出了一个新的目标函数,可以实现小批量的多个 epochs 更新。〔!!注意这里 不是 回合episodes,是深度学习中常见的 epochs,完整的数据集送入到神经网络训练并且返回称为一次 epoch〕
The new methods, which we call
proximal policy optimization (PPO), have some of the benefits of trust region policy optimization (TRPO), but they are much simpler to implement, more general, and have better sample complexity (empirically). 【方法的优势】我们称之为 近端策略优化(PPO) 的新方法具有信任域策略优化(TRPO)的一些优点,但它们更容易实现,更通用,并且具有更好的样本复杂度 (经验)。
Our experiments test PPO on a collection of benchmark tasks, including simulated robotic locomotion and Atari game playing, and we show that PPO outperforms other online policy gradient methods, and overall strikes a favorable balance between sample complexity, simplicity, and wall-time. 【实验 及 评估结果】
我们的实验在一系列基准任务(包括模拟机器人运动 和 Atari雅达利 游戏)上对 PPO 进行了测试,结果表明 PPO 优于其他在线策略梯度方法 ,总体上在样本复杂性、简单性和操作时间之间取得了良好的平衡。【这里的 wall time 是指什么的时间?】 ------> 更快收敛
1 引言
In recent years, several different approaches have been proposed for reinforcement learning with neural network function approximators. 【现在利用...解决...问题有哪些方法】
近年来,人们提出了几种使用 神经网络函数近似器 的强化学习方法。
The leading contenders are deep Q-learning [Mni+15], "vanilla" policy gradient methods [Mni+16], and trust region / natural policy gradient methods [Sch+15b].
主要的竞争者是 深度 Q 学习deep Q-learning [Mni+15],"朴素" 策略梯度方法[Mni+16]和信任域/自然策略梯度方法[Sch+15b]。
However, there is room for improvement in developing a method that is scalable (to large models and parallel implementations), data efficient, and robust (i.e., successful on a variety of problems without hyperparameter tuning). 【哪些方面还有改进空间】
然而,在开发 可扩展的(针对 大型模型和并行实现)、数据效率和 鲁棒性 (即,在没有超参数调优的情况下成功处理各种问题) 的方法方面仍有改进的空间。
Q-learning (with function approximation) fails on many simple problems1 and is poorly understood, vanilla policy gradient methods have poor data effiency and robustness; and trust region policy optimization (TRPO) is relatively complicated, and is not compatible with architectures that include noise (such as dropout) or parameter sharing (between the policy and value function, or with auxiliary tasks). 【这些方法的不足】
Q-learning (带函数近似)在许多简单问题上失败了,并且很难理解,朴素策略梯度方法的数据效率和鲁棒性较差;信任域策略优化 (TRPO) 相对复杂,不兼容 包含噪声(如 dropout )或 参数共享(策略和价值函数之间,或与辅助任务之间) 的架构。
- 脚注:
1 While DQN works well on game environments like the Arcade Learning Environment [Bel+15] with discrete action spaces, it has not been demonstrated to perform well on continuous control benchmarks such as those in OpenAI Gym [Bro+16] and described by Duan et al. [Dua+16].
虽然 DQN 在具有离散动作空间的游戏环境如 Arcade Learning Environment街机学习环境) 等游戏环境中表现良好,但它在连续控制基准(如 OpenAI Gym [Bro+16] 和 Duan 等人描述的 [Dua+16]) 中表现不佳。
↓ 【提出的算法 的关键 idea】
This paper seeks to improve the current state of affairs by introducing an algorithm that attains the data efficiency and reliable performance of TRPO, while using only first-order optimization.
本文试图通过一种算法来改善现状,该算法在仅使用一阶优化的情况下,实现了 TRPO 的数据效率和可靠性能。
We propose a novel objective with clipped probability ratios, which forms a pessimistic estimate(i.e., lower bound) of the performance of the policy.
我们提出了一种带有裁剪概率比 的新目标,它形成了策略性能的一个悲观估计(即 下界)。
To optimize policies, we alternate between sampling data from the policy and performing several epochs of optimization on the sampled data.
为了优化策略,我们在 从策略中采样数据 和 基于采样好的数据执行多个回合的优化 之间交替进行。
↓ 【比较实验的结果】
Our experiments compare the performance of various different versions of the surrogate objective, and find that the version with the clipped probability ratios performs best.
我们的实验比较了各种不同版本的代理目标的性能,发现具有裁剪概率比的版本性能最好。
We also compare PPO to several previous algorithms from the literature.
我们还比较了 PPO 与先前文献中的几种算法。
On continuous control tasks, it performs better than the algorithms we compare against.
在连续控制任务 中,它比我们比较的算法表现 得更好 。
On Atari, it performs significantly better (in terms of sample complexity) than A2C and similarly to ACER though it is much simpler.
在雅达利上,它的表现明显好于 A2C(就 样本复杂度 而言),与 ACER 相似,然而它简单得多。
2 背景:策略优化
2.1 策略梯度方法
Policy gradient methods work by computing an estimator of the policy gradient and plugging it into a stochastic gradient ascent algorithm.
策略梯度方法通过计算 策略梯度的估计值 并将其插入随机梯度上升算法来工作。
The most commonly used gradient estimator has theform
最常用的梯度估计器 有如下形式
~
g ^ = E ^ t [ ∇ θ log π θ ( a t ∣ s t ) A ^ t ] ( 1 ) \hat g=\hat {\mathbb E}t\Big[\nabla\theta\log\pi_\theta(a_t|s_t)\hat A_t\Big]~~~~~~~~~~(1) g^=E^t[∇θlogπθ(at∣st)A^t] (1)
~式中 π θ π_\theta πθ 是随机策略, A ^ t \hat A_t A^t 是时间步 t t t 处的优势函数的估计量。
期望 E ^ t [ ⋯ ] \hat {\mathbb E}_t[\cdots] E^t[⋯] 表示在采样和优化之间交替的算法中,有限批样本的经验平均值。
使用自动微分软件的实现 通过构造一个目标函数来工作,该目标函数的梯度是策略梯度估计量;
通过求目标函数的微分得到估计量 g ^ \hat g g^
~
L P G ( θ ) = E ^ t [ log π θ ( a t ∣ s t ) A ^ t ] ( 2 ) L^{PG}(\theta)=\hat {\mathbb E}t\Big[\log\pi\theta(a_t|s_t)\hat A_t\Big]~~~~~~~~~~(2)~~~~ LPG(θ)=E^t[logπθ(at∣st)A^t] (2) 比式 (1) 少了 ∇ θ \nabla_\theta ∇θ
~虽然使用相同的轨迹对损失 L P G L^{PG} LPG 执行多个优化步骤很有吸引力,但这样做是不合理的,并且经验上它通常会导致破坏性的大规模策略更新(参见第 6.1 节;结果没有显示,但与"不裁剪或处罚"设置 相似或更差)。
2.2 信任区域方法
在 TRPO [Sch+15b] 中,目标函数("代理"目标)在策略更新大小的约束下最大化。具体地说,
~
m a x i m i z e θ E ^ t [ π θ ( a t ∣ s t ) π θ o l d ( a t ∣ s t ) A ^ t ] ( 3 ) \underset{\theta}{\rm maximize}~~\hat{\mathbb E}t\Big[\frac{\pi\theta(a_t|s_t)}{\pi_{\theta_{\rm old}}(a_t|s_t)}\hat A_t\Big]~~~~~~~~~~(3) θmaximize E^t[πθold(at∣st)πθ(at∣st)A^t] (3)
~
满足 E ^ t [ K L [ π θ o l d ( ⋅ ∣ s t ) , π θ ( ⋅ ∣ s t ) ] ] ≤ δ ( 4 ) 满足~~ \hat{\mathbb E}t\Big[{\rm KL}[\pi{\theta_{\rm old}}(·|s_t),\pi_\theta(·|s_t)]\Big]\leq\delta~~~~~~~~~~(4) 满足 E^t[KL[πθold(⋅∣st),πθ(⋅∣st)]]≤δ (4)
~这里, θ o l d \theta_{\rm old} θold 是更新前的策略参数向量。
在对目标函数进行 线性近似 和 对约束进行二次近似后,利用共轭梯度算法可以有效地 近似求解 该问题。
证明 TRPO 的理论实际上建议使用惩罚而不是约束,即对于某个系数 β \beta β, 求解无约束优化问题
~
m a x i m i z e θ E ^ t [ π θ ( a t ∣ s t ) π θ o l d ( a t ∣ s t ) A ^ t ⏟ 式 ( 3 ) − β K L [ π θ o l d ( ⋅ ∣ s t ) , π θ ( ⋅ ∣ s t ) ] ⏟ 式 ( 4 ) ] ( 5 ) \underset{\theta}{\rm maximize}~~\hat{\mathbb E}t\Big[\underbrace{\frac{\pi\theta(a_t|s_t)}{\pi_{\theta_{\rm old}}(a_t|s_t)}\hat A_t}{\textcolor{blue}{式 ~(3)}}-\textcolor{blue}{\beta}~\underbrace{{\rm KL}[\pi{\theta_{\rm old}}(·|s_t),\pi_\theta(·|s_t)]}_{\textcolor{blue}{式 ~(4)}}\Big]~~~~~~~~~~(5) θmaximize E^t[式 (3) πθold(at∣st)πθ(at∣st)A^t−β 式 (4) KL[πθold(⋅∣st),πθ(⋅∣st)]] (5)
~这源于这样一个事实,即某个代理人的目标(计算状态上的最大 KL 而不是平均值)形成了策略 π π π 性能的下界(即悲观界)。
TRPO 使用硬约束而不是惩罚,因为在不同问题中很难选择表现良好的单个 β \beta β 值------甚至在单个问题中,其中特征在学习过程中发生变化。
因此,为了实现 模拟 TRPO 单调改进的一阶算法 的目标,实验表明,简单地选择一个固定的惩罚系数 β β β 并用 SGD 优化惩罚目标方程 (5) 是不够的;需要进行额外的修改。
3 裁剪的代理目标函数
令 r t ( θ ) r_t(\theta) rt(θ) 表示概率比 r t ( θ ) = π θ ( a t ∣ s t ) π θ o l d ( a t ∣ s t ) r_t(\textcolor{blue}{\theta}) = \frac{\pi_{\textcolor{blue}{\theta}}(a_t|s_t)}{\pi_{\theta_{\rm old}}(a_t|s_t)} rt(θ)=πθold(at∣st)πθ(at∣st), 则 r ( θ o l d ) = 1 r(\theta_{\rm old}) = 1 r(θold)=1。
TRPO 最大化 "surrogate" 代理 目标:
~
L C P I ( θ ) = E ^ t [ π θ ( a t ∣ s t ) π θ o l d ( a t ∣ s t ) A ^ t ] = E ^ t [ r t ( θ ) A ^ t ] ( 6 ) L^{CPI}(\theta)=\hat{\mathbb E}t\Big[\frac{\pi\theta(a_t|s_t)}{\pi_{\theta_{\rm old}}(a_t|s_t)}\hat A_t\Big]=\hat{\mathbb E}_t\Big[r_t(\theta)\hat A_t\Big]~~~~~~~~~~(6)~~ LCPI(θ)=E^t[πθold(at∣st)πθ(at∣st)A^t]=E^t[rt(θ)A^t] (6) CPI:保守策略迭代
~上标 CPI 指的是 conservative policy iteration保守策略迭代[KLO2],该目标是在其中被提出的。
如果没有约束, L C P I L^{CPI} LCPI 的最大化将导致过大的策略更新;
因此,我们现在考虑如何修改目标,以惩罚使 r t ( θ ) r_t(θ) rt(θ) 偏离 1 的策略变化。〔 鼓励 π θ \pi_\theta πθ 接近 π θ o l d \pi_{\theta_{\rm old}} πθold 〕
我们拟议的主要目标如下:
~
L C L I P ( θ ) = E ^ t [ min ( r t ( θ ) A ^ t , c l i p ( r t ( θ ) , 1 − ϵ , 1 + ϵ ) A ^ t ) ] ( 7 ) L^{CLIP}(\theta)=\hat{\mathbb E}_t\Big[\min\Big(r_t(\theta)\hat A_t,{\rm clip}\big(r_t(\theta),1-\epsilon,1+\epsilon\big)\hat A_t\Big)\Big]~~~~~~~~~~(7) LCLIP(θ)=E^t[min(rt(θ)A^t,clip(rt(θ),1−ϵ,1+ϵ)A^t)] (7)
~其中 ϵ \epsilon ϵ 是一个超参数,认为 ϵ = 0.2 \epsilon= 0.2 ϵ=0.2。
这一目标的动机如下。
min 中的第一项是 L C P I L^{CPI} LCPI。第二项 c l i p ( r t ( θ ) , 1 − ϵ , 1 + ϵ ) A ^ t {\rm clip}\big(r_t(\theta),1-\epsilon,1+\epsilon\big)\hat A_t clip(rt(θ),1−ϵ,1+ϵ)A^t 通过裁剪概率比来修改代理目标,
这避免 r t r_t rt 移到区间 [ 1 − ϵ , 1 + ϵ ] [1-\epsilon,1+\epsilon] [1−ϵ,1+ϵ] 之外。
最后,我们取裁剪目标和未裁剪目标的最小值,因此最终目标是未裁剪目标的下界 (即悲观界)。
在这种方案中,只有当概率比的变化 对目标有利时,我们才忽略它;
当概率比的变化 对目标不利时,我们才考虑它。
请注意,当 θ θ θ 为 θ o l d θ_{\rm old} θold 附近的一阶(即 r = 1) 时, L C L I P ( θ ) = L C P I ( θ ) L^{CLIP}(\theta) = L^{CPI}(\theta) LCLIP(θ)=LCPI(θ) ,
然而,当 θ θ θ 远离 θ o l d θ_{\rm old} θold 时,它们变得不同。
图 1 绘制了 L C L I P L^{CLIP} LCLIP 中的单个项(即单个 t);
请注意,根据优势是正的还是负的,概率比 r r r 被裁剪为 1 − ϵ 1 - \epsilon 1−ϵ 或 1 + ϵ 1 + \epsilon 1+ϵ。

图 1: 图片显示 代理函数 L C L I P L^{CLIP} LCLIP 的一项(即单个时间步长)作为正优势(左)和负优势(右)的概率比 r 的函数的图。
每个图上的红色圆圈表示优化的起点,即 r = 1。
注意, L C L I P L^{CLIP} LCLIP 对这些项中的很多项进行了求和。
图 2 提供了关于代理目标 L C L I P L^{CLIP} LCLIP 的另一个直觉来源。它显示了当我们沿着策略更新方向插值时,几个目标是如何变化的,这是通过对连续控制问题的近端策略优化 PPO (我们将很快介绍的算法)获得的。
我们可以看到, L C L I P L^{CLIP} LCLIP 是 L C P I L^{CPI} LCPI 的下界,因为策略更新太大而受到惩罚。

图 2: 当我们在初始策略参数 θ o l d \theta_{\rm old} θold 和更新后的策略参数之间插入 代理目标,更新的策略参数是我们在一次 PPO 迭代后计算的。
更新后的策略 与 初始策略的 KL 差异约为 0.02,这是 L C L I P L^{CLIP} LCLIP 最大的点。
该图对应于 Hopper-vl 问题的第一个策略更新,使用第 6.1 节提供的超参数。
4 自适应 KL 惩罚系数
另一种方法,可以作为裁剪代理目标函数的替代方法,或者作为它的补充,是对 KL 散度使用惩罚,并调整惩罚系数,以便我们在每次策略更新时达到 KL 散度 d t a r g d_{\rm targ} dtarg 的某个目标值。
在我们的实验中,我们发现 KL 惩罚比 裁剪代理目标函数 表现得更差,但是,我们在这里包括它,因为它是一个重要的基线。
在这个算法的最简单实例中,我们在每个策略更新中执行以下步骤:
- 通过 小批量 SGD 的 几个 回合epochs,对 KL-惩罚目标进行优化:
~
L K L P E N ( θ ) = E ^ t [ π θ ( a t ∣ s t ) π θ o l d ( a t ∣ s t ) A ^ t − β K L [ π θ o l d ( ⋅ ∣ s t ) , π θ ( ⋅ ∣ s t ) ] ] ⏟ 式 ( 5 ) ( 8 ) L^{KLPEN}(\theta)=\underbrace{\hat{\mathbb E}t\Big[\frac{\pi\theta(a_t|s_t)}{\pi_{\theta_{\rm old}}(a_t|s_t)}\hat A_t-\beta~{\rm KL}[\pi_{\theta_{\rm old}}(·|s_t),\pi_\theta(·|s_t)]\Big]}_{\textcolor{blue}{式 ~(5)}}~~~~~~~~~~(8) LKLPEN(θ)=式 (5) E^t[πθold(at∣st)πθ(at∣st)A^t−β KL[πθold(⋅∣st),πθ(⋅∣st)]] (8)
~- 计算 d = E ^ t [ K L [ π θ o l d ( ⋅ ∣ s t ) , π θ ( ⋅ ∣ s t ) ] ] d=\hat{\mathbb E}t\Big[{\rm KL}[\pi{\theta_{\rm old}}(·|s_t),\pi_\theta(·|s_t)]\Big] d=E^t[KL[πθold(⋅∣st),πθ(⋅∣st)]]
~
~~~~~~~~~~ 如果 d < d t a r g 1.5 d<\frac{d_{\rm targ}}{1.5} d<1.5dtarg, β ← β 2 \beta\leftarrow\frac{\beta}{2} β←2β
~~~~~~~~~~ 如果 d > d t a r g × 1.5 d>d_{\rm targ}\times 1.5 d>dtarg×1.5, β ← β × 2 \beta\leftarrow \beta \times 2 β←β×2
~
更新后的 β \beta β 用于下一次策略更新。
在这个方案中,当 KL 散度与 d t a r g d_{\rm targ} dtarg 显著不同时,我们偶尔会看到策略更新,然而,这些是罕见的,且 β \beta β 会迅速调整。
上述参数 1.5 和 2 是启发式选择的,但算法对它们不是很敏感。
β \beta β 的初始值是另一个超参数,但在实践中并不重要,因为算法会快速调整它。
5 算法
通过对典型的 策略梯度实现 进行微小的更改,可以计算和区分前几节中的代理损失。
对于使用自动微分的实现,只需构造损失 L C L I P L^{CLIP} LCLIP 或 L K L P E N L^{KLPEN} LKLPEN 代替 L P G L^{PG} LPG,并 在此目标上 执行 随机梯度上升的多个步骤。
大多数计算 方差减少的优势函数估计 的技术都使用 习得的状态-价值函数 V ( s ) V(s) V(s);例如,广义优势估计[Sch+15a],或者 [Mni+16]中的有限视界估计。
如果使用 在策略和价值函数之间共享参数的神经网络架构,我们必须使用结合策略代理和价值函数误差项的损失函数。
这一目标可以通过添加 熵奖励 来进一步增强,以确保充分的探索,正如过去的工作所建议的那样[Wil92;Mni + 16]。
结合这些项,我们得到以下的目标函数,每次迭代(近似)最大化:
~
L t C L I P + V F + S ( θ ) = E ^ t [ L t C L I P ( θ ) − c 1 L t V F ( θ ) + c 2 S [ π θ ] ( s t ) ] ( 9 ) L_t^{CLIP+VF+S}(\theta)=\hat{\mathbb E}t\Big[L_t^{CLIP}(\theta)-c_1L_t^{VF}(\theta)+c_2S[\pi\theta](s_t)\Big]~~~~~~~~~~(9)~~~ LtCLIP+VF+S(θ)=E^t[LtCLIP(θ)−c1LtVF(θ)+c2S[πθ](st)] (9) VF: 价值函数
~其中 c 1 , c 2 c_1,c_2 c1,c2 是系数, S S S 表示熵补贴 entropy bonus, L t V F L^{VF}t LtVF 是平方误差损失 ( V θ ( s t ) − V t t a r g ) 2 (V\theta(s_t) - V_t^{\rm targ})^2 (Vθ(st)−Vttarg)2。
策略梯度实现的一种风格,在 [Mni+16] 中普及开来,非常适合与循环神经网络一起使用,它在 T T T 个时间步 (其中 T T T 远小于回合长度) 上运行策略,并使用收集的样本进行更新。这种风格需要一个不超过 时间步 T T T 的优势估计器。[Mni+16] 使用的估计器是
~
A ^ t = − V ( s t ) + r t + γ r t + 1 + ⋯ + γ T − t + 1 r T − 1 + γ T − t V ( s T ) ( 10 ) \hat A_t=-V(s_t)+r_{\textcolor{blue}{t}}+\gamma r_{t+1}+\cdots+\gamma^{T-t+1}r_{\textcolor{blue}{T-1}}+\gamma^{T-t}V(s_T)~~~~~~~~~~(10) A^t=−V(st)+rt+γrt+1+⋯+γT−t+1rT−1+γT−tV(sT) (10)
~其中 t t t 为给定长度为 T T T 的轨迹段 [ 0 , T ] [0,T] [0,T] 中的时间索引。
将这一选择一般化,我们可以使用裁剪版的广义优势估计,当 λ = 1 λ=1 λ=1 时,可简化为式 (10):
~
A ^ t = Δ t + ( γ λ ) Δ t + 1 + ⋯ + ( γ λ ) T − t + 1 Δ T − 1 ( 11 ) \hat A_t=\Delta_t+(\gamma\lambda)\Delta_{t+1}+\cdots+(\gamma\lambda)^{T-t+1}\Delta_{T-1}~~~~~~~~~~(11) A^t=Δt+(γλ)Δt+1+⋯+(γλ)T−t+1ΔT−1 (11)
~其中 Δ t = r t + γ V ( s t + 1 ) − V ( s t ) ( 12 ) ~~\Delta_t=r_t+\gamma V(s_{t+1})-V(s_t)~~~~~~~~~~(12) Δt=rt+γV(st+1)−V(st) (12)
~
一个使用 固定长度轨迹段 的 近端策略优化(PPO)算法如下所示。每次迭代, N N N 个 (并行) actors ,每个都收集 长度为 T T T 个 时间步 的数据。
然后,我们在这些数据的 N T NT NT 时间步上构建代理损失,并使用 minibatch SGD(或者通常为了更好的性能,Adam [KB14]) 对 K K K 个 回合epoches 进行优化。

算法: PPO, Actor-Critic Style
f o r {\bf for} for 迭代 = 1 , 2 , ⋯ d o 1,2,\cdots~{\bf do} 1,2,⋯ do
~~~~~~ f o r a c t o r = 1 , 2 , ⋯ , N d o {\bf for} ~{\rm actor}=1,2,\cdots, N~{\bf do} for actor=1,2,⋯,N do
~~~~~~~~~~~ 在环境中运行策略 π θ o l d \pi_{\theta_{\rm old}}~ πθold T T T 个时间步。
~~~~~~~~~~~ 计算优势估计 A ^ 1 , ⋯ , A ^ T \hat A_1,\cdots,\hat A_T A^1,⋯,A^T
~~~~~~ e n d f o r {\bf end~ for} end for
~~~~~~ 用 K K K 个epochs和 批大小 M ≤ N T M\leq NT M≤NT,优化 关于 θ \theta θ 的 代理目标函数 L L L
θ o l d ← θ ~~~~~~\theta_{\rm old}\leftarrow\theta θold←θ
e n d f o r {\bf end~ for} end for
6 实验
6.1 代理目标 比较
首先,我们比较了不同超参数下的几种不同代理目标。
在这里,我们将代理目标 L C L I P L^{CLIP} LCLIP 与几种自然变体和消融版本进行比较。
| 类型 | 目标函数 |
|---|---|
| 没有裁剪或惩罚 | L t ( θ ) = r t ( θ ) A ^ t L_t(\theta)=r_t(\theta)\hat A_t Lt(θ)=rt(θ)A^t |
| 裁剪 | L t ( θ ) = min ( r t ( θ ) A ^ t , c l i p ( r t ( θ ) , 1 − ϵ , 1 + ϵ ) A ^ t ) L_t(\theta)=\min\Big(\textcolor{blue}{r_t(\theta)\hat A_t},{\rm clip}\big(r_t(\theta),1-\epsilon,1+\epsilon\big)\hat A_t\Big) Lt(θ)=min(rt(θ)A^t,clip(rt(θ),1−ϵ,1+ϵ)A^t) |
| KL 惩罚 (固定 或 自适应) | L t ( θ ) = r t ( θ ) A ^ t − β K L [ π θ o l d , π θ ] L_t(\theta)=\textcolor{blue}{r_t(\theta)\hat A_t}-\beta ~{\rm KL}[\pi_{\theta_{\rm old}},\pi_\theta] Lt(θ)=rt(θ)A^t−β KL[πθold,πθ] |
对于 KL 惩罚,可以使用 固定的惩罚系数 β \beta β 或 自适应系数,如第 4 节所述,使用目标 KL 值 d t a r g d_{\rm targ} dtarg。
请注意,我们也尝试了在 log 中进行裁剪,但发现性能并没有提高。
因为我们正在为每个算法变体搜索超参数,所以我们选择了一个计算成本较低的基准来测试算法。也就是说,我们使用在 OpenAI Gym [Bro+16] 中实现的 7 个模拟机器人任务,它使用 MuJoCo [TET12] 物理引擎。
- 脚注:
2HalfCheetah,Hopper, InvertedDoublePendulum, InvertedPendulum, Reacher, Swimmer 和 Walker2d,都是"-v1"我们对每一个都进行了一百万步的训练。
除了我们搜索的用于裁剪 ( ϵ \epsilon ϵ) 和 KL 惩罚 ( β , d t a r g ) (\beta, d_{\rm targ}) (β,dtarg) 的超参数外,其他超参数在 表 3 中提供。

为了表示策略,我们使用了一个具有 两个 64 单元隐藏层 的全连接 MLP,以及 tanh 非线性,输出高斯分布的平均值,具有可变的标准差,参考 [Sch+15b;Dua + 16]。
我们不共享 策略和价值函数之间 的参数(所以 系数 c 1 c_1 c1 是无关的),我们不使用熵补贴entropy bonus。
每个算法在所有 7 个环境中运行,每个环境中有 3 个随机种子。我们通过计算最后 100 个回合的平均总奖励来对算法的每次运行进行评分。我们变换和缩放每个环境的分数,以便随机策略 给出 0 分 ,将最佳结果 设置为 1 ,并在 21 次运行中取平均值,为每个算法设置生成单个标量。
结果如表 1 所示。请注意,在没有裁剪或惩罚的情况下,分数是负的,因为对于一个环境( half cheetah),它会导致一个非常负的分数,这比最初的随机策略更糟糕。
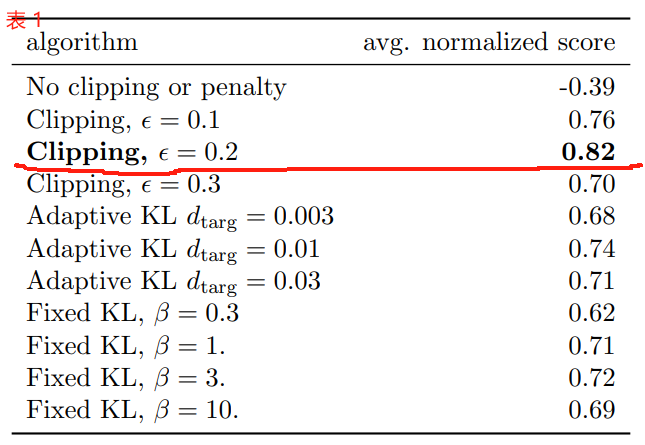
表 1: 连续控制基准的结果。
每个算法/超参数设置的平均归一化分数(算法运行超过 21 次,在 7 个环境中)。 β \beta β 初始化为 1。
6.2 连续域 与其它算法比较
接下来,我们将 PPO (用第 3 节中的"裁剪的"代理目标 )与文献中的其他几种方法进行比较,这些方法被认为对连续问题有效。
我们比较了以下算法的调过的实现: 信任域策略优化[Sch+15b],交叉熵方法(CEM) [SL06],自适应步长的朴素策略梯度3,A2C [Mni+16],具有信任域的 A2C [Wan+16]。
- 脚注:
3 在每批数据之后,根据原始和更新策略的 KL 散度调整 Adam 步长,使用类似于第 4 节所示的规则。实现可参考: https://github.com/berkeleydeeprlcourse/homework/tree/master/hw4A2C 表示优势演员评论家advantage actor critic,是 A3C 的同步版本,我们发现它的性能与异步版本相同或更好。
对于 PPO,我们使用了前一节中的超参数,其中 ϵ \epsilon ϵ = 0.2。
我们看到,PPO 几乎 在所有的 连续控制环境中都优于以前的方法。 〔 在 任务 Swimmer-v1 不如 TRPO 〕

6.3 连续域示例: 人形跑步和转向
To showcase the performance of PPO on high-dimensional continuous control problems, we train on a set of problems involving a 3D humanoid, where the robot must run, steer, and get up off the ground, possibly while being pelted by cubes.
为了展示 PPO 在高维连续控制问题上的表现,我们在一组涉及 3D 人形机器人的问题上进行训练,其中机器人在可能被立方体投掷时必须跑动,转向并离开地面。
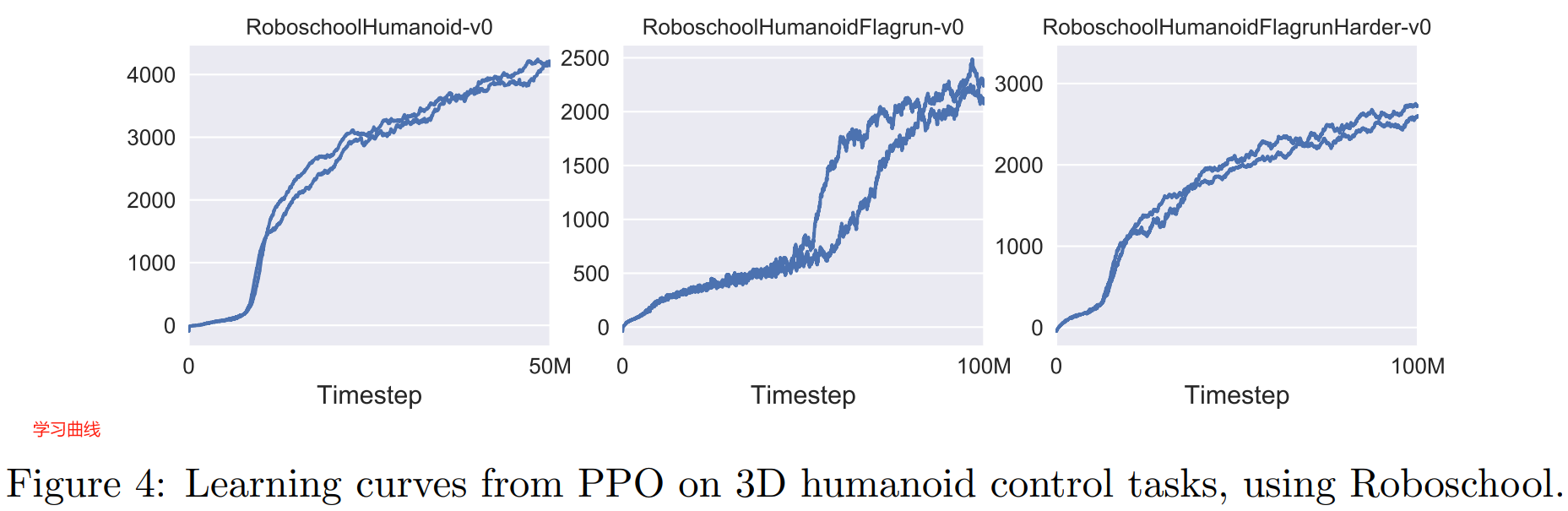
The three tasks we test on are (1) RoboschoolHumanoid: forward locomotion only, (2) RoboschoolHumanoidFlagrun: position of target is randomly varied every 200 timesteps or whenever the goal is reached, (3) RoboschoolHumanoidFlagrunHarder, where the robot is pelted by cubes and needs to get up off the ground.
我们测试的三个任务是:
(1) RoboschoolHumanoid: 只向前移动;(2) RoboschoolHumanoidFlagrun: 目标位置每 200 个时间步 或者每当达到目标时 随机变化;(3) RoboschoolHumanoidFlagrunHarder: 机器人被立方体猛砸,需要离开地面。
See Figure 5 for still frames of a learned policy, and Figure 4 for learning curves on the three tasks.
Hyperparameters are provided in Table 4.
图 5 显示了习得的策略的静态框架,图 4 显示了三个任务的学习曲线。
表 4 提供了超参数。
In concurrent work, Heess et al. [Hee+17] used the adaptive KL variant of PPO (Section 4) to learn locomotion policies for 3D robots.
在并行工作中,Heess 等人[Hee+17]使用 PPO 的自适应 KL 变体(章节 4)来学习 3D 机器人的运动策略。


6.4 在 Atari 域 与其它算法的比较
We also ran PPO on the Arcade Learning Environment [Bel+15] benchmark and compared against well-tuned implementations of A2C [Mni+16] and ACER [Wan+16].
我们还在 街机学习环境the Arcade Learning Environment [Bel+15] 基准上运行 PPO,并与 A2C [Mni+16] 和 ACER [Wan+16] 的调整好的实现进行比较。
For all three algorithms, we used the same policy network architechture as used in [Mni+16].
The hyperparameters for PPO are provided in Table 5.
对于这三种算法,我们使用了与 [Mni+16] 中使用的 相同的策略网络架构。
表 5 提供了 PPO 的超参数。
For the other two algorithms, we used hyperparameters that were tuned to maximize performance on this benchmark.
对于另外两种算法,我们使用了经过调优的超参数,以获得此基准测试的最大化性能。

A table of results and learning curves for all 49 games is provided in Appendix B. We considerthe following two scoring metrics: (1) average reward per episode over entire training period (which favors fast learning), and (2) average reward per episode over last 100 episodes of training (which favors final performance).
附录 B 提供了所有 49 款游戏的结果表和学习曲线。
我们考虑以下两个评分指标:
(1) 整个训练期间每个回合的平均奖励(有利于快速学习);
(2) 整个训练期间最后 100 个回合每个回合的平均奖励(有利于最终性能)。Table 2 shows the number of games "won" by each algorithm, where wecompute the victor by averaging the scoring metric across three trials.
表 2 显示了每种算法"获胜"的游戏数量,其中我们通过在三次试验中平均得分指标来计算胜利者。

7 结论
We have introduced proximal policy optimization, a family of policy optimization methods that use multiple epochs of stochastic gradient ascent to perform each policy update.
我们介绍了近端策略优化,这是一系列 使用随机梯度上升的多个回合 来执行每次策略更新 的策略优化方法。
These methods have the stability and reliability of trust-region methods but are much simpler to implement, requiring only few lines of code change to a vanilla policy gradient implementation, applicable in more general settings (for example, when using a joint architecture for the policy and value function), and have better overall performance.
这些方法具有 信任区域方法 的稳定性 和可靠性 ,但实现起来要简单 得多,只需要将几行代码更改为朴素策略梯度实现,适用于更一般的设置(例如,在为 策略和价值函数 使用联合架构时),并且具有更好的整体性能。
8 致谢
感谢 Rocky Duan, Peter Chen 和 OpenAI 其他人富有见地的评论。
参考文献
附录
A 超参数
已插入正文相应位置
B 雅达利Atari 游戏上的更多表现
这里我们将 PPO 与 A2C 在 49 款雅达利游戏中进行比较。图 6 显示了三种随机种子各自的学习曲线,表 6 显示了平均性能。



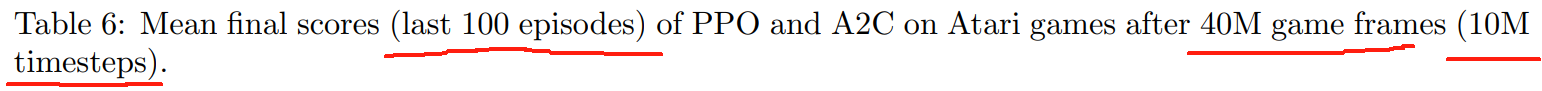
1、 在 任务 Krull 中 A2C 表现更好。


2、PPO 并不是在所有任务中都是表现得最好的,部分任务 ACER 表现更好。


