【智能算法应用】人工水母搜索算法求解二维路径规划问题

摘要

本文应用人工水母搜索算法（Jellyfish Search, JFS）求解二维空间中的路径规划问题。水母搜索算法是一种新型的智能优化算法，灵感来源于水母的群体运动行为，通过模仿水母的觅食、漂浮等行为，实现全局最优路径的搜索。本文在MATLAB平台上实现了该算法，并通过一系列复杂环境下的仿真实验验证了其在路径规划中的有效性和收敛性。

理论

1. 路径规划问题

在二维路径规划中，给定起始点和目标点，要求在复杂环境中找到一条避开障碍物的最短路径。该问题可以被视为全局优化问题，通过智能优化算法在空间中搜索最优解。

2. 人工水母搜索算法（JFS）

人工水母搜索算法是一种基于自然界水母行为的群体智能优化算法。该算法模拟了水母在海洋中的运动行为，包括两种基本的搜索模式：

被动漂流：水母顺着海流随机移动，增加探索空间的范围。
主动觅食：水母向食物源（目标）靠近，实现局部开发。

JFS通过这两种行为的随机组合，不断优化水母个体的位置，以达到全局最优解。算法通过以下步骤实现：

初始化水母个体的初始位置；
计算每个个体的适应度；
根据适应度更新个体的位置，模拟漂流或觅食行为；
在迭代中逐渐收敛至全局最优解。

3. 算法流程

初始种群生成：随机初始化若干个水母个体的位置。
适应度评估：根据路径的距离与碰撞情况计算每条路径的适应度。
更新规则：

被动漂流：通过随机移动更新水母的位置。
主动觅食：通过最优个体的位置引导水母移动。

收敛判定：当达到预设的迭代次数或适应度满足收敛条件时，输出最优路径。

实验结果

实验环境实验环境为二维平面空间，其中随机设置若干圆形障碍物。起点和终点分别设置在平面的一端和另一端，实验任务是找到一条从起点到终点的最短路径，并确保路径不与障碍物相交。
实验参数

水母个体数：30
最大迭代次数：300
障碍物数量：5

实验结果分析

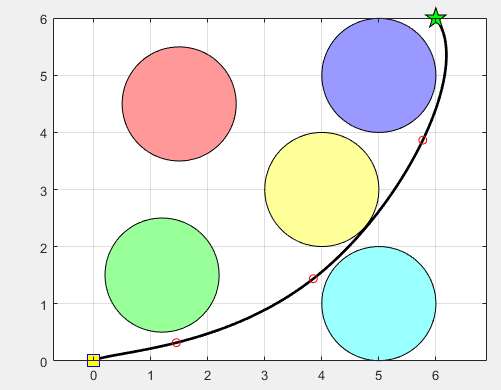
图1展示了在二维障碍物环境下的路径规划结果。黑色曲线为JFS算法找到的最优路径，避开了红色的圆形障碍物。起点用黄色方块表示，终点用绿色星形表示。
图2展示了随着迭代次数的增加，适应度值的变化趋势。可以看到，经过多次迭代后，适应度值逐渐收敛，最终稳定在最优解附近，证明该算法具有较好的收敛性和稳定性。

仿真图示

图1：二维路径规划结果
图2：适应度随迭代次数的变化曲线

部分代码

以下是实现人工水母搜索算法的部分MATLAB代码：

% Jellyfish Search (JFS) Algorithm for Path Planning in 2D
% 初始化参数
num_jellyfish = 30; % 水母个体数量
max_iterations = 300; % 最大迭代次数
bounds = [0, 6; 0, 6]; % 搜索空间边界
obstacles = [2, 4, 1; 4, 3, 1; 1, 2, 1]; % 障碍物 (x, y, radius)

% 初始化水母位置
jellyfish_positions = rand(num_jellyfish, 2) .* (bounds(:,2)' - bounds(:,1)') + bounds(:,1)';

% 适应度函数 (避障加路径长度)
fitness = @(pos) pathFitness(pos, obstacles, bounds);

% 主循环
for iter = 1:max_iterations
    for i = 1:num_jellyfish
        % 计算适应度
        current_fitness = fitness(jellyfish_positions(i, :));
        
        % 更新水母位置 (随机漂流或向目标点靠近)
        new_position = updateJellyfishPosition(jellyfish_positions(i, :), bounds, iter, max_iterations);
        new_fitness = fitness(new_position);
        
        % 如果新位置更优，则更新位置
        if new_fitness < current_fitness
            jellyfish_positions(i, :) = new_position;
        end
    end
    
    % 记录最优解
    best_fitness(iter) = min(arrayfun(fitness, jellyfish_positions));
end

% 绘制路径和障碍物
figure;
plotPath(jellyfish_positions, obstacles, bounds);

% 绘制适应度曲线
figure;
plot(1:max_iterations, best_fitness);
xlabel('迭代次数');
ylabel('适应度');
title('适应度随迭代次数变化');

参考文献

❝

Mirjalili, S., & Lewis, A. (2016). The whale optimization algorithm. Advances in Engineering Software, 95, 51-67.

Kennedy, J., & Eberhart, R. C. (1995). Particle swarm optimization. Proceedings of ICNN'95 - International Conference on Neural Networks, 4, 1942-1948.

Holland, J. H. (1992). Adaptation in Natural and Artificial Systems. MIT Press.

（文章内容仅供参考，具体效果以图片为准）