前言
数据结构在学什么?
- 如何用程序代码把现实世界的问题信息化
- 如何用计算机高效地处理这些信息从而创造价值
第一章:数据结构在学什么?
总览

什么是数据?
简介:数据是信息的载体 ,是描述客观事物属性的数、字符及所有能输入到计算机中并被计算机程序识别和处理的符号的集合,数据是计算机加工的原料。
数据元素、数据项
数据元素:
是数据的基本单位,通常作为一个整体进行考虑和处理。
数据项:
一个数据元素可有若干个数据项组成,数据项是构成数据元素的不可分割的最小单位。
什么是数据对象
数据对象:
是具有相同性质的数据元素的集合,是数据的一个子集
数据结构
数据结构:
是相互之间存在一种或多种特定关系的数据元素的集合。
分类:
线性数据结构(xx排行榜)、网状数据结构(xx好友关系图)
同一个数据对象中的数据元素,可以组成不同的数据结构
数据结构三要素
三要素:
逻辑结构
分类:集合结构、线性结构(一对一)、树形结构(一对多)、图状结构(多对多)
数据的运算
物理结构(存储结构)
逻辑结构
集合结构
集合:
各个元素同属于一个集合,别无其他关系

线性结构
线性结构:
数据元素之间是一对一的关系
除了第一个元素,所有元素都有唯一的前驱
除了最后一个元素,所有元素都有唯一的后继

树形结构
树形结构:
数据元素之间是一对多的关系

图状结构
图状结构:
数据元素之间是多对多的关系
数据的运算
简介:针对与某种逻辑结构,结合实际需求,定义基本运算
- 针对线性结构存在的基本运算
- 查找第I个数据元素
- 在第I个位置插入新的元素
- 删除第I个元素
物理结构(存储结构)
数据的存储结构:
顺序存储
链式存储
索引存储
散列存储
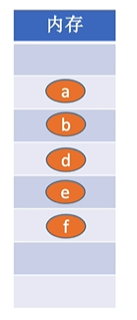
顺序存储
说明:使用线性结构举例
把逻辑上相邻的元素存储在物理位置上也相邻的存储单元中,元素之间的关系有存储单元的邻接关系来体现。
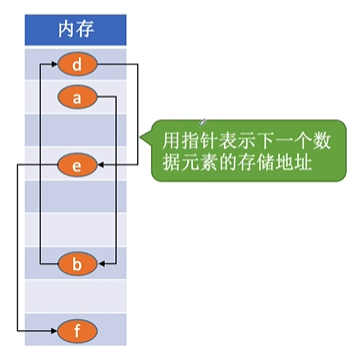
链式存储
说明:使用线性结构举例
链式存储:
逻辑上相邻的元素在物理位置上可以不相邻,借助指示元素存储地址的指针来表示元素之间的逻辑关系。
索引存储
说明:使用线性结构举例
索引存储:
在存储元素信息的同时,还建立附加的索引表,在索引表中的每一项称为索引项,索引项形式为:(关键字,地址)

散列存储
散列存储:
根据元素的关键字直接计算出该元素的存储地址,又称为哈希存储。
数据类型、抽象数据类型
数据类型:
是一个值的集合和定义在此集合上的一组操作的总称。
数据类型分类:
原子类型(值不可再分的数据类型):bool、int类型
结构类型(值可以再分为若干成分):结构体类型
抽象数据类型:
是抽象数据组织与之先关的操作
算法基本概念
知识总览:

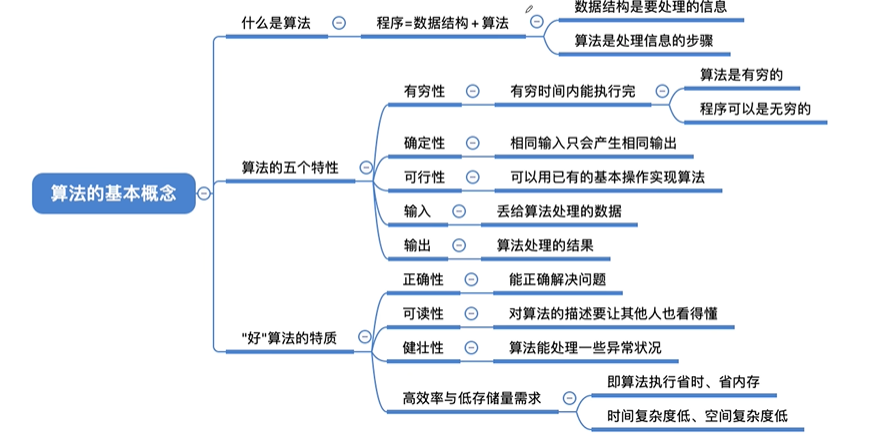
什么是算法?
程序= 数据结构 + 算法
举例说明:番茄炒蛋
数据结构等于:食材
算法等于:完成番茄炒蛋的具体步骤(求解问题的步骤)
算法的五个特性
有穷性:必须在固定的时间或步骤中完成所走的步骤
确定性:算法处理的程序结果永远是一致的,不存在多种结果的情况。
可行性;算法中描述的操作都可以通过已实现的基本运算执行有限次来实现。
输入:一个算法有0个或多个输入,
输出:一个算法有-个或多个输出。
好算法的特质
正确性:可以正确的解决问题
可读性:具有良好的可读性,帮助人们好理解
健壮性:遇到非法数据时,能够适当的作出反应应对,而不会产生奇怪的结果。
高效率:算法执行时间快,时间复杂度低
低存储量需求:空间复杂度低,不费内存
算法效率的度量
时间复杂度
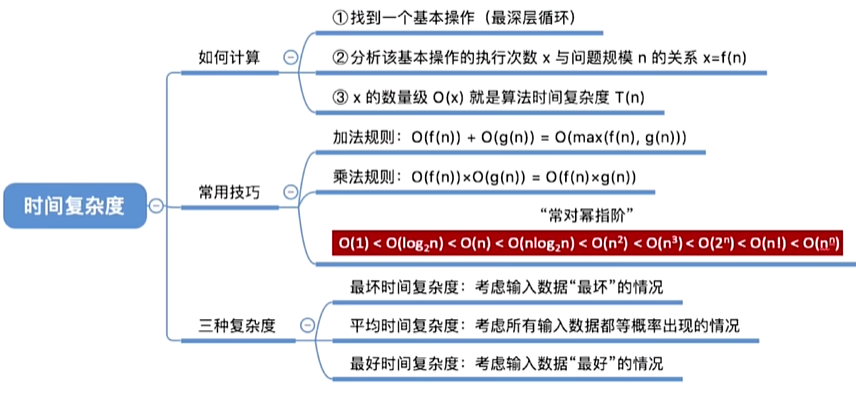 时间复杂度:
事前预估算法时间开销**T(n)**与问题规模n的关系(T 表示 Time)
- 案例分析1
c
/**
T(3000) = 1 +3001+2*3000+1
时间开销与问题规模n的关系:
T(n) = 3n+3= O(n) // 常数阶直接用n
结论一:顺序执行的代码只会影响常数项,可以忽略
结论二:只需挑循环中一个基本操作,分析它的执行次数与n的关系即可。
结论三:如果有多层嵌套循环,只需关注最深层循环了几次
*/
#include <stdio.h>
void loveYou(int num ) {
int i = 1;
while(i<=num) {
printf("%d\n", i);
i++;
}
printf("exit");
}
int main() {
loveYou(3000);
return 0;
}- 案例分析2

- 时间复杂度简化过程
如果时间复杂度项过于长的话,可以保留最高项
结论:当问题规模n足够大时,可以只考虑阶数高的部分

简化为:

- 比较阶数更高的项:

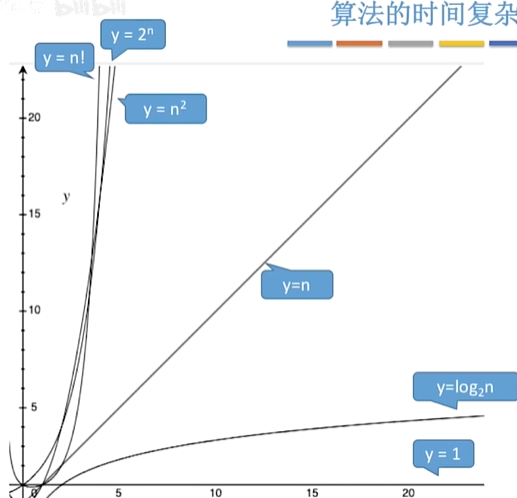
- 练习题1

- 练习题2

- 总结
时间复杂度度量标准:
最坏时间复杂度:最坏情况下算法的时间复杂度
平均时间复杂度:所有输入示例等概率出现的情况下,算法的期望运行时间
最好时间复杂度(参考意义不大):最好情况下算法的时间复杂度
空间复杂度

空间复杂度:衡量内存空间开销与问题规模n之间的关系
程序空间复杂度分析:只需要关注存储空间大小与问题规模相关的变量
- 案例分析1:
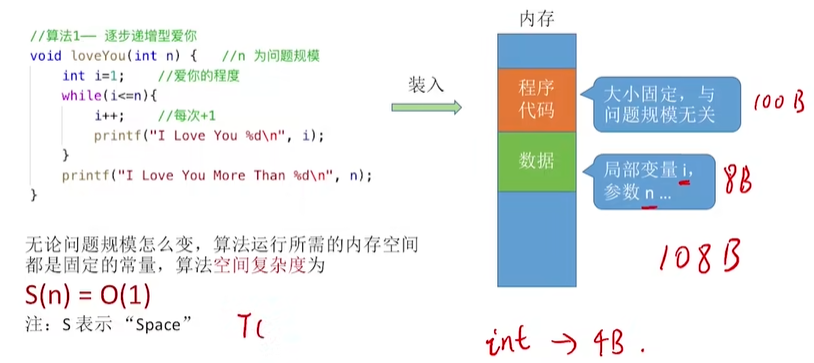
- 案例分析2:
程序空间复杂度分析:只需要关注存储空间大小与问题规模相关的变量

- 案例分析3
分析:4nn+4+4
S(O)=o(n的二次方)
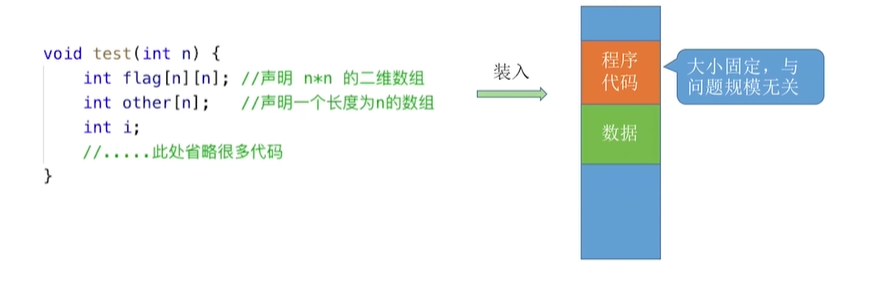
- 案例分析4
分析:4nn+4*n+4+4
S(O)=o(N的二次方)

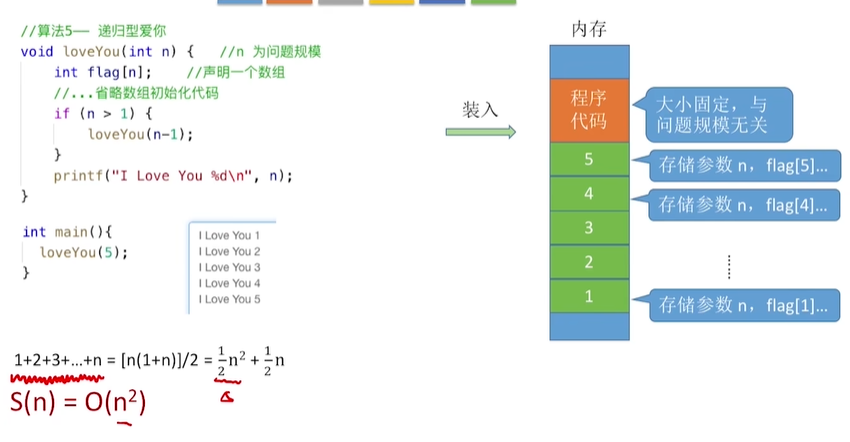
- 案例分析5:
分析:
递归第一次:5,a,b,c
递归第二次:4,a,b,c
递归第三次:4,a,b,c
...
S(O)=O(n)
总结:空阿复杂度=递归调用的深度
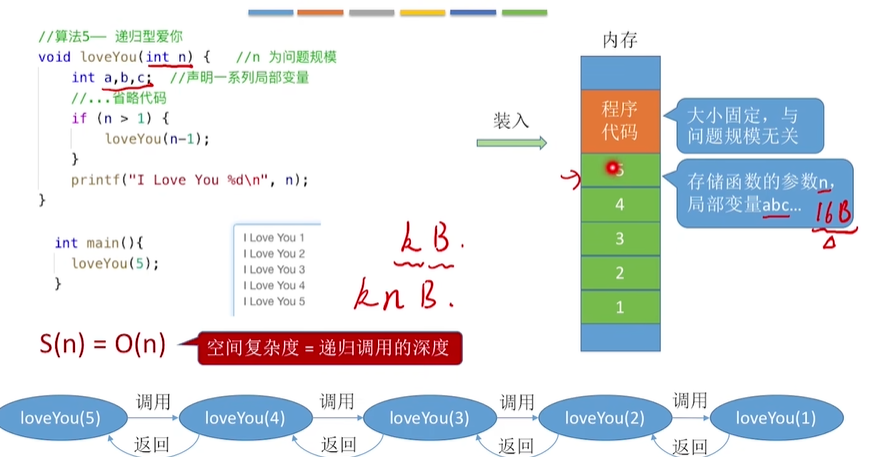
- 案例分析5修改: