654. Maximum Binary Tree

You are given an integer array nums with no duplicates. A maximum binary tree can be built recursively from nums using the following algorithm:

Create a root node whose value is the maximum value in nums.
Recursively build the left subtree on the subarray prefix to the left of the maximum value.
Recursively build the right subtree on the subarray suffix to the right of the maximum value.

Return the maximum binary tree built from nums.

Example 1:

复制代码

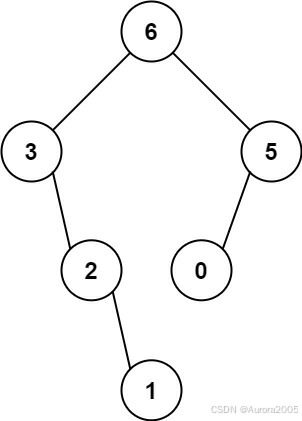
Input: nums = [3,2,1,6,0,5]
Output: [6,3,5,null,2,0,null,null,1]
Explanation: The recursive calls are as follow:
- The largest value in [3,2,1,6,0,5] is 6. Left prefix is [3,2,1] and right suffix is [0,5].
    - The largest value in [3,2,1] is 3. Left prefix is [] and right suffix is [2,1].
        - Empty array, so no child.
        - The largest value in [2,1] is 2. Left prefix is [] and right suffix is [1].
            - Empty array, so no child.
            - Only one element, so child is a node with value 1.
    - The largest value in [0,5] is 5. Left prefix is [0] and right suffix is [].
        - Only one element, so child is a node with value 0.
        - Empty array, so no child.

Example 2:

复制代码

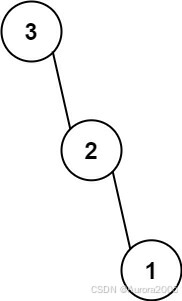
Input: nums = [3,2,1]
Output: [3,null,2,null,1]

Constraints:

1 <= nums.length <= 1000
0 <= nums[i] <= 1000
All integers in nums are unique.

class Solution {
public:
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
TreeNode*node=new TreeNode(0);
//是否叶节点
if(nums.size()==1){
node->val=nums[0];
return node;
}
//找到数组最大值及其下标
int maxValue=0;//因为数组元素大于等于1
int maxValueIndex=0;
for(int i=0;i<nums.size();i++){
if(maxValue<nums[i]){
maxValue=nums[i];
maxValueIndex=i;
}
}
node->val=maxValue;
//最大值所在的下标左区间，构造左子树
if(maxValueIndex>0){
vector<int>newVec(nums.begin(),nums.begin()+maxValueIndex);
node->left=constructMaximumBinaryTree(newVec);
}
//最大值所在的下标右区间，构造右子树
if(maxValueIndex<nums.size()-1){
vector<int>newVec(nums.begin()+maxValueIndex+1,nums.end());
node->right=constructMaximumBinaryTree(newVec);
}
```
      return node;
  }
```
};

注意：

1，前提条件

1）二叉树

2，解题流程

PS ：这里的代码及其流程存在缺陷，与 106/105 题一样，重复定义过多 vector ，浪费空间，后续熟练之后再进行优化，这个版本代码比较利于理解

1）先做，后做

第一步，梳理题意，这道题本身不是很难，主要的难点就是如何判断哪一部分构造左子树，哪一部分构造右子树。
- 第二步，new一个node存储数组最大值为根节点
- 第三步，判断叶节点
  - 也就是nums的size==1
  - 不要忘记给node赋值和return
- 第四步，找到数组的最大值及其下标
  - 把maxValue的初始值设为0（原因：数组元素大于等于1），maxValueIndex也为0
  - for循环找到maxValue和MaxValueIndex
  - 给node赋值
- 第五步，根据最大值左区间，构造左子树
  - 条件：MaxValue>0
  - 新数组，newVec（begin，begin+MaxValueIndex）
  - 递归
- 第六步，根据最大值右区间，构造右子树
  - 条件：MaxValue<nums.size()-1
  - 新数组，newVec（begin+MaxValueIndex+1，end）
  - 递归
- 第七步，return node

2）知识点套路

递归
判断叶节点
判断左右子树及其范围

3）前提

4）注意点

判断完叶节点后不要忘记给node赋值
for循环找到MaxValue和MaxValueIndex之后也要赋值