450. Delete Node in a BST

Given a root node reference of a BST and a key, delete the node with the given key in the BST. Return the root node reference (possibly updated) of the BST.

Basically, the deletion can be divided into two stages:

Search for a node to remove.
If the node is found, delete the node.

Example 1:

复制代码

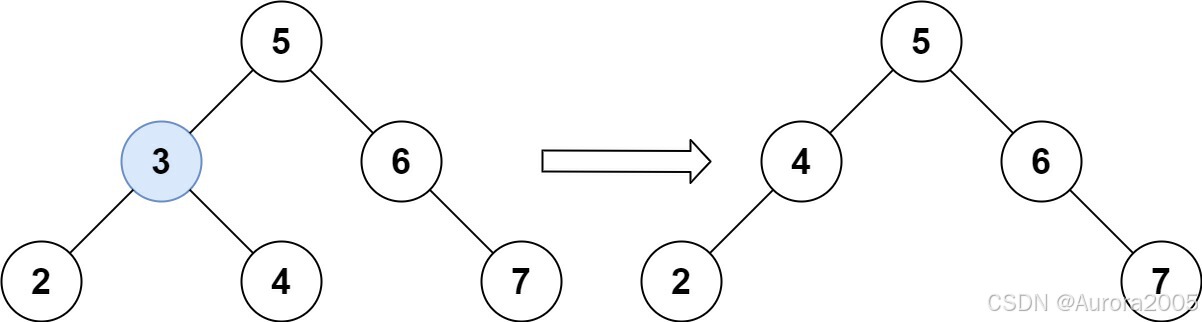
Input: root = [5,3,6,2,4,null,7], key = 3
Output: [5,4,6,2,null,null,7]
Explanation: Given key to delete is 3. So we find the node with value 3 and delete it.
One valid answer is [5,4,6,2,null,null,7], shown in the above BST.
Please notice that another valid answer is [5,2,6,null,4,null,7] and it's also accepted.

Example 2:

复制代码

Input: root = [5,3,6,2,4,null,7], key = 0
Output: [5,3,6,2,4,null,7]
Explanation: The tree does not contain a node with value = 0.

Example 3:

复制代码

Input: root = [], key = 0
Output: []

Constraints:

The number of nodes in the tree is in the range [0, 104].
-105 <= Node.val <= 105
Each node has a unique value.
root is a valid binary search tree.
-105 <= key <= 105

Follow up: Could you solve it with time complexity O(height of tree)?

class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        //第一种情况，没有找到要删除的节点
        if(root==NULL)return root;
        if(root->val==key){
            //第二种情况：找到要删除的节点，其左右孩子都为空
            if(root->left==NULL && root->right==NULL){
                delete root;
                return NULL;
            }
            //第三种情况：左空，右不空
            else if(root->left==NULL && root->right!=NULL){
                auto node=root->right;
                delete root;
                return node;
            }
            //第四种情况：左不空，右空
            else if(root->left!=NULL && root->right==NULL){
                auto node=root->left;
                delete root;
                return node;
            }
            //第五种情况：左右都不空
            else{
                TreeNode*node=root->right;
                while(node->left!=NULL){
                    node=node->left;
                }
                node->left=root->left;
                TreeNode*temp=root;
                root=root->right;
                delete temp;
                return root;
            }
        }
        if(root->val>key)root->left=deleteNode(root->left,key);
        if(root->val<key)root->right=deleteNode(root->right,key);
        return root;
    }
};

注意点：这里用的是递归，迭代不太适合初学者，故略过

1，先做，后做

在说明解题步骤之前，我们需要先明确，删除的节点一共会有5种情况：

1）没找到要删除的节点

找到了：

2）要删除的节点是叶节点，没有左右孩子

3）要删除的节点的左孩子为空，右孩子不空

4）要删除的节点的左孩子不为空，右孩子为空

5）要删除的节点的左右孩子都不空，那么这时候就需要把左孩子赋值到右孩子的最左边节点的左子树

第一步（情况1），root如果为空，返回root

第二步，root->val==key

1）（情况2）直接删除root，返回NULL

2）（情况3）先新建一个node=root->right，再删除root，返回node

3）（情况4）同理

4）（情况5）

先新建一个node=root->right

while循环找到node最左边的节点（坑点见注意点1））

把root->left赋值到node->left

用temp保存root

Root=root->right，就是把右孩子作为新的root

Delete root

返回node

第三步，递归

1）如果root的val小了，就递归右子树，并将递归的结果赋给root->right

2）大了同理

第四步，return root

2，知识点套路

1）其实最主要的就是分清这5种情况

2）二叉搜索树的特性（左子树<root->val<右子树）

3，前提条件：二叉搜索树（其实也可以当成普通二叉树来找，但是思路就比较绕，不太适合我这种初学者，故略过）

4，注意点

1）第五种情况中的while(node->left!=NULL)，不是while（node!=NULL）这样的话，循环出来Node=NULL

2）注意别把root->val==key写成root==key