【LeetCode】109. 有序链表转换二叉搜索树

文章目录

• [109. 有序链表转换二叉搜索树](#109. 有序链表转换二叉搜索树)
• • 题目描述
  • [示例 1:](#示例 1:)
  • [示例 2:](#示例 2:)
  • 提示:
  • 解题思路
  • • 问题分析
    • [方法一：快慢指针 + 递归（最优解）](#方法一：快慢指针 + 递归（最优解）)
    • 方法二：转换为数组
    • 方法三：中序遍历模拟（最巧妙）
    • [方法四：递归 + 计算长度](#方法四：递归 + 计算长度)
    • 复杂度对比
    • 关键技巧总结
    • 与108题对比
    • 扩展问题
    • 相关题目
  • 完整题解代码

109. 有序链表转换二叉搜索树

题目描述

给定一个单链表的头节点 head ，其中的元素 按升序排序 ，将其转换为 平衡 二叉搜索树。

示例 1:

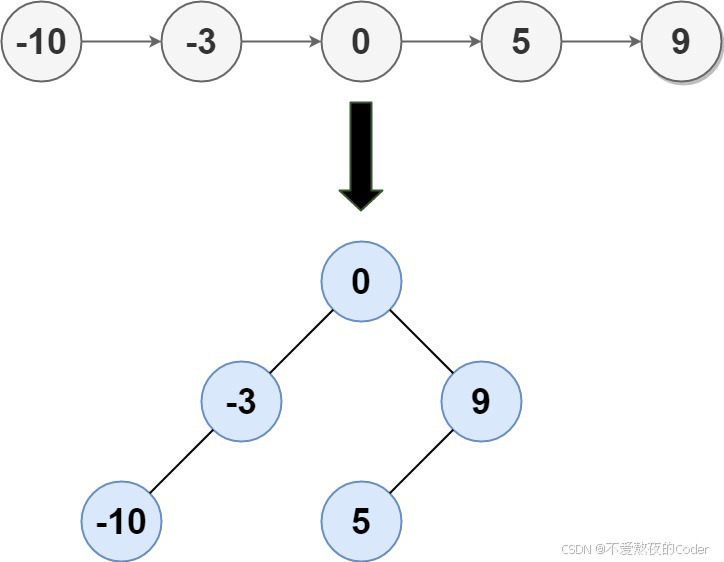
输入: head = [-10,-3,0,5,9]

输出: [0,-3,9,-10,null,5]

解释: 一个可能的答案是[0，-3,9，-10,null,5]，它表示所示的高度平衡的二叉搜索树。

示例 2:

输入: head = []

输出: []

提示:

• head 中的节点数在[0, 2 * 104] 范围内
• -10^5 <= Node.val <= 10^5

解题思路

问题分析

这道题是 LeetCode 108 的升级版，核心差异：

维度	108题	109题
数据结构	有序数组	有序链表
访问方式	O(1)随机访问	O(n)顺序访问
找中点	直接计算索引	需要遍历/快慢指针
难度提升	⭐⭐	⭐⭐⭐

关键挑战：链表无法像数组那样 O(1) 访问中间元素！

方法一：快慢指针 + 递归（最优解）

核心思想 ：使用快慢指针找链表中点，然后递归构建

graph TD A[输入: -10→-3→0→5→9] --> B[快慢指针找中点] B --> C[slow指向0, 断开链表] C --> D[左半: -10→-3] C --> E[中点: 0] C --> F[右半: 5→9] E --> G[创建根节点 val=0] D --> H[递归处理左半链表] F --> I[递归处理右半链表] H --> J[左子树: -3为根] I --> K[右子树: 5为根] style A fill:#e1f5ff style E fill:#bbdefb style G fill:#90caf9 style J fill:#c8e6c9 style K fill:#c8e6c9

快慢指针找中点技巧：
否 是 输入: head链表 slow = head
fast = head
prev = nil fast != nil &&
fast.Next != nil? 找到中点: slow prev = slow
slow = slow.Next
fast = fast.Next.Next 断开链表
prev.Next = nil 返回: 左半链表, 中点, 右半链表

算法步骤：

1. 边界处理：链表为空或只有一个节点
2. 找中点：快指针走2步，慢指针走1步
3. 断开链表：将链表分为左半和右半
4. 递归构建 ：
   • 创建根节点（中点值）
   • 递归处理左半链表 → 左子树
   • 递归处理右半链表 → 右子树

代码实现：

func sortedListToBST(head *ListNode) *TreeNode {
    if head == nil {
        return nil
    }
    if head.Next == nil {
        return &TreeNode{Val: head.Val}
    }
    
    // 快慢指针找中点
    slow, fast, prev := head, head, (*ListNode)(nil)
    for fast != nil && fast.Next != nil {
        prev = slow
        slow = slow.Next
        fast = fast.Next.Next
    }
    
    // 断开链表
    prev.Next = nil
    
    // 构建树
    root := &TreeNode{Val: slow.Val}
    root.Left = sortedListToBST(head)      // 左半链表
    root.Right = sortedListToBST(slow.Next) // 右半链表
    
    return root
}

时间复杂度：O(n log n)

• 每层递归需要 O(n) 时间找中点
• 递归深度 O(log n)

空间复杂度：O(log n) - 递归栈

方法二：转换为数组

核心思想：先将链表转为数组，然后用108题的方法

flowchart LR A[链表: -10→-3→0→5→9] --> B[遍历转数组] B --> C[数组: -10,-3,0,5,9] C --> D[108题方法构建BST] D --> E[返回根节点] style A fill:#e1f5ff style C fill:#bbdefb style E fill:#c5cae9

优缺点分析：

维度	评价
实现难度	⭐ 简单，复用108题代码
时间复杂度	O(n) 遍历 + O(n) 构建 = O(n) ✅
空间复杂度	O(n) 数组存储 ❌
适用场景	空间充足、追求简洁

方法三：中序遍历模拟（最巧妙）

核心洞察 ：BST的中序遍历恰好是有序序列！

算法思路：

1. 先统计链表长度 n
2. 按中序遍历顺序构建树（左-根-右）
3. 用全局指针记录当前链表节点

统计链表长度 n=5 中序构建 0, n-1 递归左子树 0, 1 创建节点 val=链表当前值 指针后移 递归右子树 3, 4

为什么有效？

链表: -10 → -3 → 0 → 5 → 9
      ↑
中序遍历顺序构建树时，依次消费链表节点

时间复杂度 ：O(n) - 每个节点访问一次 ✅
空间复杂度：O(log n) - 递归栈

方法四：递归 + 计算长度

优化思路：避免每次都找中点

1. 先遍历一次计算链表总长度
2. 递归时传递子链表的起始位置和长度
3. 根据长度计算中点位置

复杂度对比

方法	时间复杂度	空间复杂度	优点	缺点
快慢指针	O(n log n)	O(log n)	直观易懂	重复遍历
转数组	O(n)	O(n)	简单快速	额外空间
中序遍历	O(n)	O(log n)	最优解	较难理解
计算长度	O(n)	O(log n)	避免重复	需要预处理

关键技巧总结

1. 快慢指针找中点：

   slow, fast := head, head
   for fast != nil && fast.Next != nil {
       slow = slow.Next
       fast = fast.Next.Next
   }
   // slow 指向中点

2. 断开链表：需要记录 prev 指针

3. 中序遍历技巧：全局指针顺序消费链表节点

4. 长度计算优化：避免重复遍历

与108题对比

维度	108题（数组）	109题（链表）
找中点	O(1)计算索引	O(n)快慢指针
分割	O(1)传递索引	O(1)断开链表
总复杂度	O(n)	O(n log n) 或 O(n)
实现难度	⭐⭐	⭐⭐⭐

扩展问题

1. 如果链表是循环链表怎么办？
2. 如何在O(n)时间、O(1)空间完成？（不计递归栈）
3. 如果要求构建完全二叉搜索树？
4. 如何处理链表中有重复元素的情况？

相关题目

• LeetCode 108：有序数组转BST（前置题）
• LeetCode 110：平衡二叉树
• LeetCode 876：链表的中间结点
• LeetCode 1382：将BST变平衡

完整题解代码

package main

import (
	"fmt"
	"math"
)

// ListNode 链表节点定义
type ListNode struct {
	Val  int
	Next *ListNode
}

// TreeNode 二叉树节点定义
type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

// ==================== 方法一：快慢指针 + 递归 ====================
// 时间复杂度：O(n log n)，每层递归O(n)找中点，深度O(log n)
// 空间复杂度：O(log n)，递归栈深度
func sortedListToBST(head *ListNode) *TreeNode {
	// 边界条件
	if head == nil {
		return nil
	}
	if head.Next == nil {
		return &TreeNode{Val: head.Val}
	}

	// 使用快慢指针找中点
	slow, fast := head, head
	var prev *ListNode

	for fast != nil && fast.Next != nil {
		prev = slow
		slow = slow.Next
		fast = fast.Next.Next
	}

	// 断开链表：prev.Next = nil
	if prev != nil {
		prev.Next = nil
	}

	// 创建根节点（中点）
	root := &TreeNode{Val: slow.Val}

	// 递归构建左右子树
	root.Left = sortedListToBST(head)       // 左半链表
	root.Right = sortedListToBST(slow.Next) // 右半链表

	return root
}

// ==================== 方法二：转换为数组 ====================
// 时间复杂度：O(n)，遍历一次链表 + 构建树
// 空间复杂度：O(n)，数组存储
func sortedListToBST2(head *ListNode) *TreeNode {
	// 链表转数组
	nums := []int{}
	curr := head
	for curr != nil {
		nums = append(nums, curr.Val)
		curr = curr.Next
	}

	// 使用108题的方法构建BST
	return arrayToBST(nums, 0, len(nums)-1)
}

func arrayToBST(nums []int, left, right int) *TreeNode {
	if left > right {
		return nil
	}

	mid := left + (right-left)/2
	root := &TreeNode{Val: nums[mid]}

	root.Left = arrayToBST(nums, left, mid-1)
	root.Right = arrayToBST(nums, mid+1, right)

	return root
}

// ==================== 方法三：中序遍历模拟（最优解）====================
// 时间复杂度：O(n)，每个节点访问一次
// 空间复杂度：O(log n)，递归栈
func sortedListToBST3(head *ListNode) *TreeNode {
	// 计算链表长度
	length := 0
	curr := head
	for curr != nil {
		length++
		curr = curr.Next
	}

	// 使用全局指针，按中序遍历顺序消费链表节点
	return inorderBuild(&head, 0, length-1)
}

func inorderBuild(head **ListNode, left, right int) *TreeNode {
	if left > right {
		return nil
	}

	mid := left + (right-left)/2

	// 先构建左子树（中序遍历：左-根-右）
	leftTree := inorderBuild(head, left, mid-1)

	// 创建根节点，消费当前链表节点
	root := &TreeNode{Val: (*head).Val}
	*head = (*head).Next // 指针后移

	// 再构建右子树
	root.Left = leftTree
	root.Right = inorderBuild(head, mid+1, right)

	return root
}

// ==================== 方法四：递归 + 计算长度优化 ====================
// 时间复杂度：O(n)
// 空间复杂度：O(log n)
func sortedListToBST4(head *ListNode) *TreeNode {
	// 计算链表长度
	length := getLength(head)
	return buildWithLength(head, length)
}

func getLength(head *ListNode) int {
	length := 0
	for head != nil {
		length++
		head = head.Next
	}
	return length
}

func buildWithLength(head *ListNode, length int) *TreeNode {
	if length == 0 {
		return nil
	}
	if length == 1 {
		return &TreeNode{Val: head.Val}
	}

	// 找到中点位置
	mid := length / 2

	// 移动到中点
	curr := head
	for i := 0; i < mid; i++ {
		curr = curr.Next
	}

	// 创建根节点
	root := &TreeNode{Val: curr.Val}

	// 递归构建左右子树
	root.Left = buildWithLength(head, mid)
	root.Right = buildWithLength(curr.Next, length-mid-1)

	return root
}

// ==================== 辅助函数 ====================

// 创建链表
func createList(nums []int) *ListNode {
	if len(nums) == 0 {
		return nil
	}

	head := &ListNode{Val: nums[0]}
	curr := head

	for i := 1; i < len(nums); i++ {
		curr.Next = &ListNode{Val: nums[i]}
		curr = curr.Next
	}

	return head
}

// 打印链表
func printList(head *ListNode) {
	fmt.Print("[")
	for head != nil {
		fmt.Print(head.Val)
		if head.Next != nil {
			fmt.Print(" -> ")
		}
		head = head.Next
	}
	fmt.Print("]")
}

// 中序遍历验证BST
func inorderTraversal(root *TreeNode) []int {
	if root == nil {
		return []int{}
	}
	result := []int{}
	result = append(result, inorderTraversal(root.Left)...)
	result = append(result, root.Val)
	result = append(result, inorderTraversal(root.Right)...)
	return result
}

// 层序遍历
func levelOrder(root *TreeNode) []interface{} {
	if root == nil {
		return []interface{}{}
	}

	result := []interface{}{}
	queue := []*TreeNode{root}

	for len(queue) > 0 {
		node := queue[0]
		queue = queue[1:]

		if node == nil {
			result = append(result, nil)
		} else {
			result = append(result, node.Val)
			queue = append(queue, node.Left)
			queue = append(queue, node.Right)
		}
	}

	// 移除末尾的 nil
	for len(result) > 0 && result[len(result)-1] == nil {
		result = result[:len(result)-1]
	}

	return result
}

// 检查是否为平衡二叉树
func isBalanced(root *TreeNode) bool {
	return checkHeight(root) != -1
}

func checkHeight(root *TreeNode) int {
	if root == nil {
		return 0
	}

	leftHeight := checkHeight(root.Left)
	if leftHeight == -1 {
		return -1
	}

	rightHeight := checkHeight(root.Right)
	if rightHeight == -1 {
		return -1
	}

	if abs(leftHeight-rightHeight) > 1 {
		return -1
	}

	return max(leftHeight, rightHeight) + 1
}

// 检查是否为BST
func isValidBST(root *TreeNode) bool {
	return validateBST(root, math.MinInt64, math.MaxInt64)
}

func validateBST(root *TreeNode, min, max int) bool {
	if root == nil {
		return true
	}

	if root.Val <= min || root.Val >= max {
		return false
	}

	return validateBST(root.Left, min, root.Val) && validateBST(root.Right, root.Val, max)
}

// 获取树的高度
func getHeight(root *TreeNode) int {
	if root == nil {
		return 0
	}
	return max(getHeight(root.Left), getHeight(root.Right)) + 1
}

// 树形打印
func printTree(root *TreeNode, prefix string, isLeft bool) {
	if root == nil {
		return
	}

	fmt.Print(prefix)
	if isLeft {
		fmt.Print("├── ")
	} else {
		fmt.Print("└── ")
	}
	fmt.Println(root.Val)

	if root.Left != nil || root.Right != nil {
		if root.Left != nil {
			printTree(root.Left, prefix+getTreePrefix(isLeft, true), true)
		} else {
			fmt.Println(prefix + getTreePrefix(isLeft, true) + "├── nil")
		}

		if root.Right != nil {
			printTree(root.Right, prefix+getTreePrefix(isLeft, false), false)
		} else {
			fmt.Println(prefix + getTreePrefix(isLeft, false) + "└── nil")
		}
	}
}

func getTreePrefix(isLeft, hasNext bool) string {
	if isLeft {
		return "│   "
	}
	return "    "
}

func abs(x int) int {
	if x < 0 {
		return -x
	}
	return x
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

// ==================== 测试函数 ====================

func testCase(name string, nums []int) {
	fmt.Printf("\n========== %s ==========\n", name)
	fmt.Print("输入链表: ")
	head := createList(nums)
	printList(head)
	fmt.Println()

	// 方法一：快慢指针
	head1 := createList(nums)
	root1 := sortedListToBST(head1)
	fmt.Println("\n方法一（快慢指针）:")
	fmt.Printf("层序遍历: %v\n", levelOrder(root1))
	fmt.Printf("中序遍历: %v\n", inorderTraversal(root1))
	fmt.Printf("是否平衡: %v\n", isBalanced(root1))
	fmt.Printf("是否BST: %v\n", isValidBST(root1))
	fmt.Printf("树高度: %d\n", getHeight(root1))
	fmt.Println("树结构:")
	printTree(root1, "", false)

	// 方法二：转数组
	head2 := createList(nums)
	root2 := sortedListToBST2(head2)
	fmt.Println("\n方法二（转数组）:")
	fmt.Printf("层序遍历: %v\n", levelOrder(root2))
	fmt.Printf("中序遍历: %v\n", inorderTraversal(root2))
	fmt.Printf("是否平衡: %v\n", isBalanced(root2))

	// 方法三：中序遍历（最优解）
	head3 := createList(nums)
	root3 := sortedListToBST3(head3)
	fmt.Println("\n方法三（中序遍历-最优解）:")
	fmt.Printf("层序遍历: %v\n", levelOrder(root3))
	fmt.Printf("中序遍历: %v\n", inorderTraversal(root3))
	fmt.Printf("是否平衡: %v\n", isBalanced(root3))

	// 方法四：计算长度优化
	head4 := createList(nums)
	root4 := sortedListToBST4(head4)
	fmt.Println("\n方法四（计算长度优化）:")
	fmt.Printf("层序遍历: %v\n", levelOrder(root4))
	fmt.Printf("中序遍历: %v\n", inorderTraversal(root4))
	fmt.Printf("是否平衡: %v\n", isBalanced(root4))
}

// ==================== 扩展功能 ====================

// 比较108题和109题的性能差异
func compareWithArray() {
	fmt.Println("\n========== 108题 vs 109题性能对比 ==========")

	sizes := []int{100, 1000, 5000}

	for _, size := range sizes {
		// 生成数据
		nums := make([]int, size)
		for i := 0; i < size; i++ {
			nums[i] = i
		}

		fmt.Printf("\n数据规模: %d\n", size)

		// 108题：数组方式（理论最优）
		root1 := arrayToBST(nums, 0, len(nums)-1)
		fmt.Printf("108题(数组): 树高度=%d, 理论高度=%d\n",
			getHeight(root1), int(math.Ceil(math.Log2(float64(size+1)))))

		// 109题方法一：快慢指针
		head := createList(nums)
		root2 := sortedListToBST(head)
		fmt.Printf("109题(快慢指针): 树高度=%d\n", getHeight(root2))

		// 109题方法三：中序遍历
		head = createList(nums)
		root3 := sortedListToBST3(head)
		fmt.Printf("109题(中序遍历): 树高度=%d\n", getHeight(root3))
	}
}

// 链表中点查找演示
func demonstrateFindMiddle() {
	fmt.Println("\n========== 快慢指针找中点演示 ==========")

	testCases := [][]int{
		{1, 2, 3, 4, 5},    // 奇数个
		{1, 2, 3, 4, 5, 6}, // 偶数个
		{1},                // 单个
		{1, 2},             // 两个
	}

	for _, nums := range testCases {
		head := createList(nums)
		fmt.Print("\n链表: ")
		printList(head)
		fmt.Println()

		// 找中点
		slow, fast := head, head
		var prev *ListNode

		for fast != nil && fast.Next != nil {
			prev = slow
			slow = slow.Next
			fast = fast.Next.Next
		}

		fmt.Printf("中点: %d\n", slow.Val)
		if prev != nil {
			fmt.Printf("中点前一个: %d\n", prev.Val)
		}
	}
}

// 验证所有方法生成的树是否等价
func verifyAllMethods() {
	fmt.Println("\n========== 验证所有方法的等价性 ==========")

	nums := []int{-10, -3, 0, 5, 9}
	head := createList(nums)

	methods := []struct {
		name string
		fn   func(*ListNode) *TreeNode
	}{
		{"快慢指针", sortedListToBST},
		{"转数组", sortedListToBST2},
		{"中序遍历", sortedListToBST3},
		{"计算长度", sortedListToBST4},
	}

	fmt.Print("输入: ")
	printList(head)
	fmt.Println()

	for _, method := range methods {
		h := createList(nums)
		root := method.fn(h)
		inorder := inorderTraversal(root)

		fmt.Printf("\n%s:\n", method.name)
		fmt.Printf("  中序遍历: %v\n", inorder)
		fmt.Printf("  是否平衡: %v\n", isBalanced(root))
		fmt.Printf("  是否BST: %v\n", isValidBST(root))
		fmt.Printf("  树高度: %d\n", getHeight(root))
	}
}

func main() {
	// 测试用例1：示例1
	testCase("测试用例1：基本情况", []int{-10, -3, 0, 5, 9})

	// 测试用例2：空链表
	testCase("测试用例2：空链表", []int{})

	// 测试用例3：单个元素
	testCase("测试用例3：单个元素", []int{1})

	// 测试用例4：两个元素
	testCase("测试用例4：两个元素", []int{1, 3})

	// 测试用例5：奇数个元素
	testCase("测试用例5：奇数个元素", []int{1, 2, 3, 4, 5, 6, 7})

	// 测试用例6：偶数个元素
	testCase("测试用例6：偶数个元素", []int{1, 2, 3, 4, 5, 6})

	// 测试用例7：连续数字
	testCase("测试用例7：连续数字", []int{0, 1, 2, 3, 4, 5, 6, 7, 8, 9})

	// 扩展功能测试
	compareWithArray()
	demonstrateFindMiddle()
	verifyAllMethods()
}