文章目录
前言
分块查找算法是一种结合顺序查找和索引查找的搜索方法。其核心思想是将无序元素分成若干有序块,建立索引表存储各块最大值和区间范围。查找时先通过顺序或折半方式定位索引块,再在该块内进行顺序查找。算法特点包括块内无序、块间有序。查找效率分析表明,当块数为√n时,顺序查找索引表可获得最优ASL(√n+1),而折半查找索引表则使ASL为⌈log₂(b+1)⌉+(s+1)/2。对于动态查找表,采用链式存储能有效提升插入/删除效率。该算法在特定数据分布下能显著提高查找性能。
一.分块查找的算法思想
1.算法思想
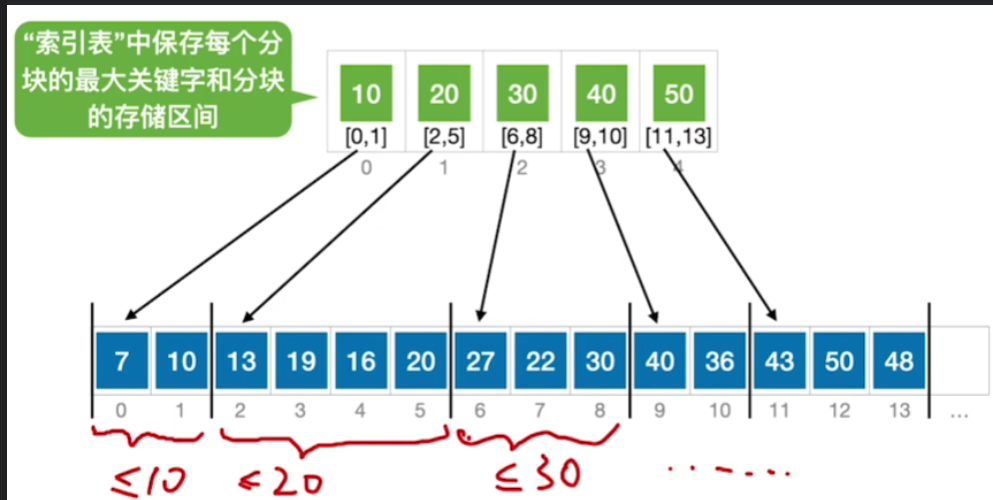
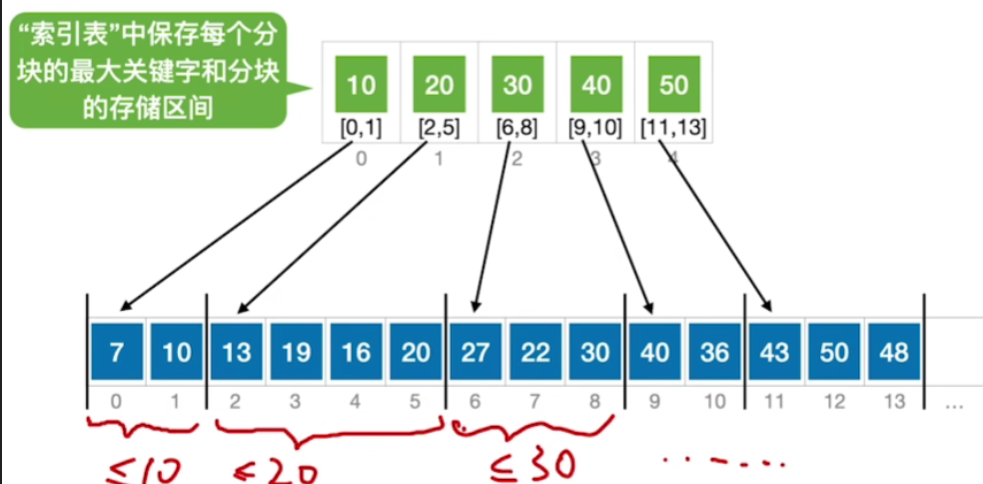
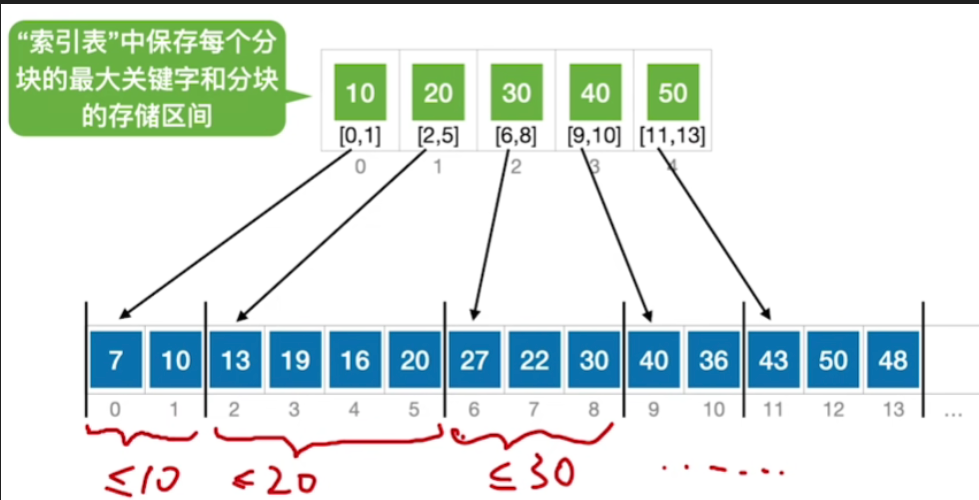
- 看似没有规律的元素,可以将他们分至一个个小区间,第一个区间内都是≤10的元素,第二个区间是≤20的元素,第三个区间是≤30的,以此类推
- 所以我们看虽然这个数组当中的某一小个部分看起来是乱序的,但是当我们把它分成一块一块的小区间之后,会发现各个区间之间其实是有序的
- 那我们可以给这个查找表,建立上一级的索引,"索引表"中保存每个分块的最大关键字和分块的存储区间
2.特点
- 块内无序、块间有序
3.代码定义
c
//索引表
typedef struct {
ElementType maxValue;// 最大的关键字
int low, high;// 分块的区间范围
}Index;
//顺序表存储实际元素
ElementType List[100];二.顺序查找查索引
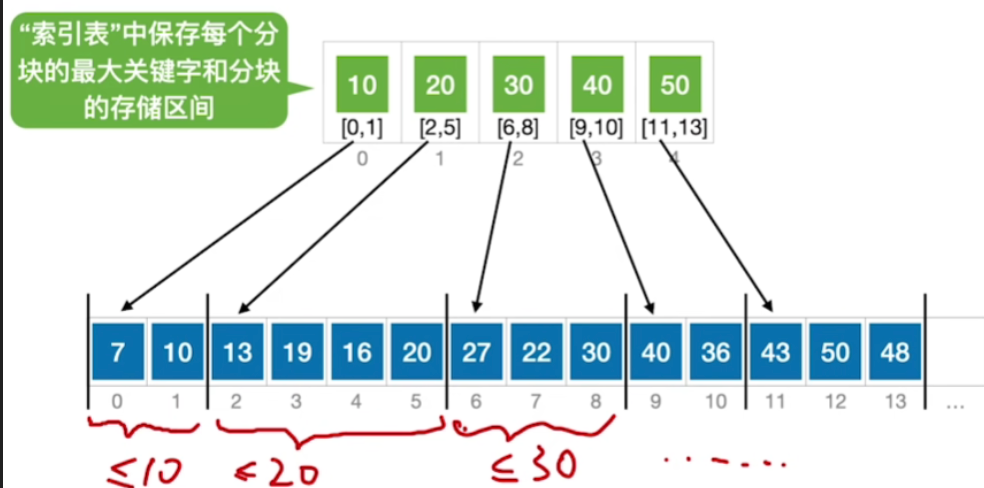
- 假设要查找的关键字是22
- 首先我们可以先查找这个索引表,从索引表的第一个元素开始依次往后找
- 那第一个元素10<22,所以肯定是在下一个分块内
- 20<22,所以还得往后找,第三个分块30是≥22的,所以如果22存在的话那么肯定是在30所指向的这个分块内
- 因此接下来就从这个方块的起始位置6开始查找
- 那6号元素不满足,所以往后找一位,接下来7号元素刚好22和我们要找的关键词是相等的,那到此为止就查找成功
- 如果这分块内的所有元素都和查找目标不同,那么说明查找失败
三.用折半查找查索引
1.查找成功
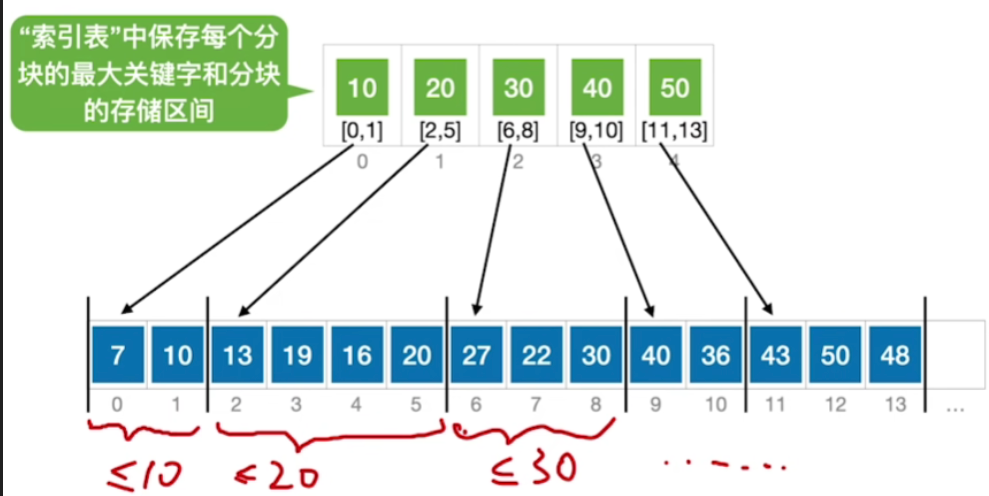
- 假设查找目标为30
- 那根据这个折半查找的规则,我们要在索引表的开头和末尾这两个元素之间尝试找到30这个关键字,那么mid等于low加high除以二,所以刚开始mid所指向的这个元素刚好就是30
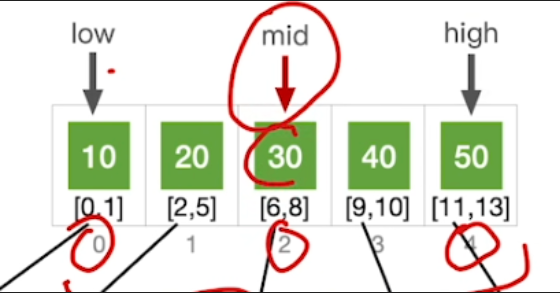
- 30指向的分块是从6开始,所以接下来会从6号元素开始往后依次的对比,那一直找到8号元素的时候查找成功
2.索引查找失败
1.给出关键字在索引表范围内
1.过程
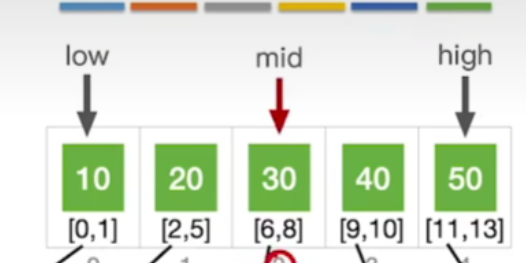
- 假设查找目标为19
- 和之前一样,mid指向low和high的中间位置
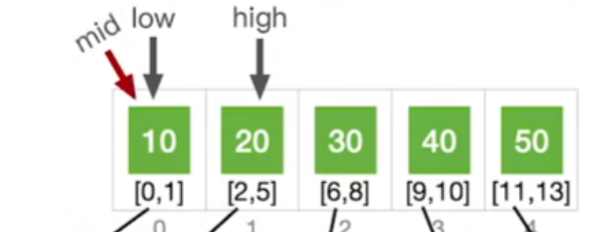
- 19<30,所以我们应该让high等于mid-1,接下来low加high除以2,那mid就应该是指向0这个位置
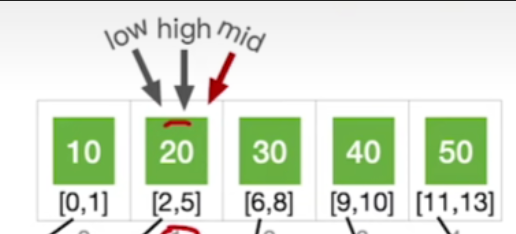
- 19>10,所以接下来我们应该让low等于mid+1同时mid等于low加high除以2
- 19<20,high = mid - 1,现在low已经大于high了,所以按照折半查找的规则,查找应该失败了,但是其实我们的19应该在在low所指向的分块中
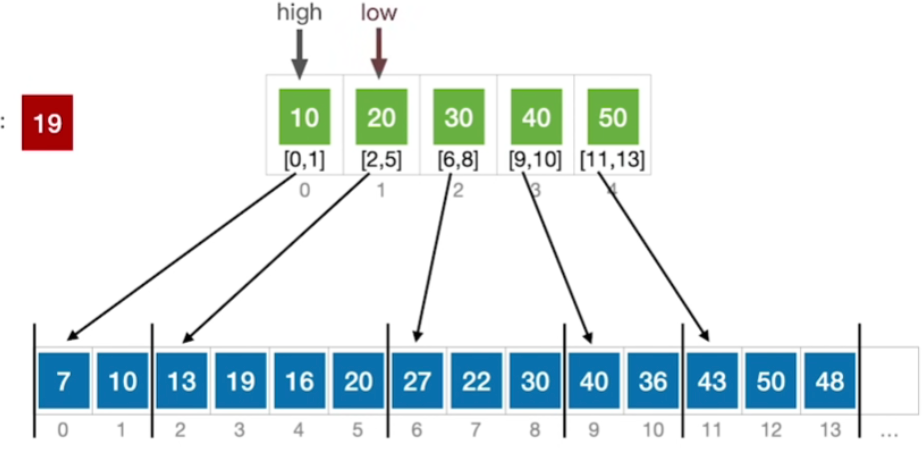
- 所以接下来应该在low所指的分块当中来查找
- 接下来的操作和之前查找成功的操作一致
2.结论
- 若索引表中不包含目标关键字,则折半查找索引表最终停在 low>high ,要在low所指分块中查找
原理:折半查找失败,最后low大于high,但是在low大于high之前的那一步,肯定是low等于high,所以如果往回退一步的话.mid和low,high肯定是指向同一个位置
此时有可能发生两种情况 k e y 是查找的目标关键字 ; m i d = { < k e y , l o w + + ① > k e y , h i g h − − ② ; \begin{aligned}key是查找的目标关键字;\\mid = \begin{cases}<key,&low++①\\>key,&high--②;\end{cases}\end{aligned} key是查找的目标关键字;mid={<key,>key,low++①high−−②;
在情况1中,low在进行自增1的操作后一定比key大
在情况2中,high自减1而low不变
所以最终low大于high的时候,low这个指针所指向的位置的这个关键字肯定是要大于key
由于在分块查找的时候,我们总是找当前分块索引比目标关键字大的元素,因此可以在low指向分块进行查找
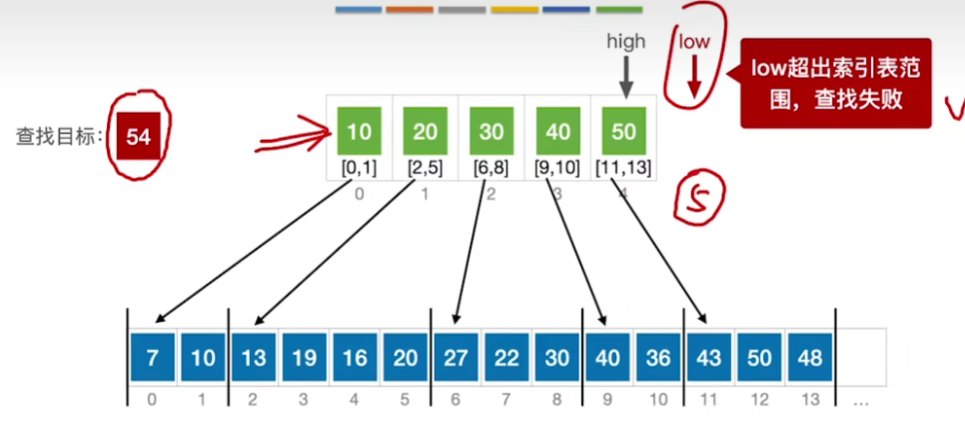
2.目标关键字超出索引范围
- 折半查找的过程和之前一样,最终结果是low超出了索引表范围,因此查找失败
四.查找效率分析(ASL)
1.一般情况
一般不考
1.分析过程
- 共有14个元素,各自被查概率为1/14
- 若索引表采用顺序查找,则7:2次、10:3次、13:3次...
- 若索引表采用折半查找,则30:4次
A S L = ∑ i = 1 n P i C i ASL=∑_{i = 1}^{n}P_iC_i ASL=i=1∑nPiCi
查找失败的情况更复杂...一般不考
2.特殊情况
1.分析过程
- 假设,长度为n的查找表被均匀地分为b块,每块s个元素
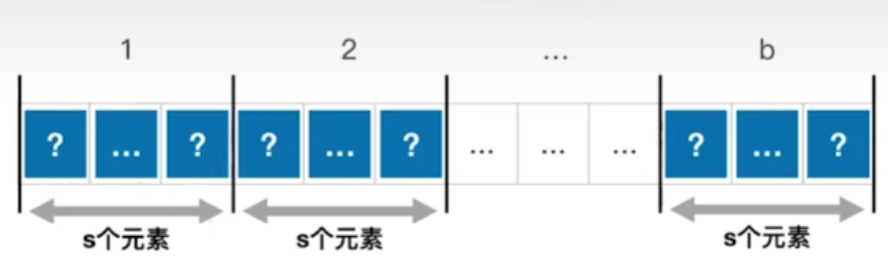
2.结论
1.总体结论
- 设索引查找和块内查找的平均查找长度分别为 L 1 、 L 2 L_{1}、L_{2} L1、L2,则分块查找的平均查找长度为
A S L = L 1 + L 2 ASL=L_{1}+L_{2} ASL=L1+L2
2.用顺序查找索引表
L I = ( 1 + 2 + ... + b ) b = b + 1 2 , L S = ( 1 + 2 + ... + s ) s = s + 1 2 ; 则 A S L = b + 1 2 + s + 1 2 = s 2 + 2 s + n 2 s 所以当 s = n 时, A S L 最小 = n + 1 ① \begin{aligned}&L_{I}=\frac{(1+2+\dotsc +b)}{b}=\frac{b+1}{2},\\&L_{S}=\frac{(1+2+\dotsc +s)}{s}=\frac{s+1}{2}; \\&则ASL=\frac{b+1}{2}+\frac{s+1}{2}=\frac{s^{2}+2s+n}{2s}\\&所以当s=\sqrt{n}时,ASL_{\text{最小}}=\sqrt{n}+1①\end{aligned} LI=b(1+2+...+b)=2b+1,LS=s(1+2+...+s)=2s+1;则ASL=2b+1+2s+1=2ss2+2s+n所以当s=n 时,ASL最小=n +1①
- 最优ASL方案 :式子①的意义在于把n个元素分为 n \sqrt{n} n 块,那么而每一个分块内有 n \sqrt{n} n 个元素,在这种情况下,可以保证ASL取得最小的值
3.用折半查找查索引表
则 L I = ⌈ log 2 ( b + 1 ) ⌉ , L S = ( 1 + 2 + ⋯ + s ) s = s + 1 2 则ASL = ⌈ log 2 ( b + 1 ) ⌉ + s + 1 2 \begin{aligned}&则L_{I}=\left\lceil\log_{2}(b+1)\right\rceil,\\&L_S=\frac{(1+2+\cdots+s)}{s}=\frac{s+1}{2}\\ &则\text{ASL}=\left\lceil\log_{2}(b+1)\right\rceil +\frac{s+1}{2}\end{aligned} 则LI=⌈log2(b+1)⌉,LS=s(1+2+⋯+s)=2s+1则ASL=⌈log2(b+1)⌉+2s+1
五.知识回顾与重要考点
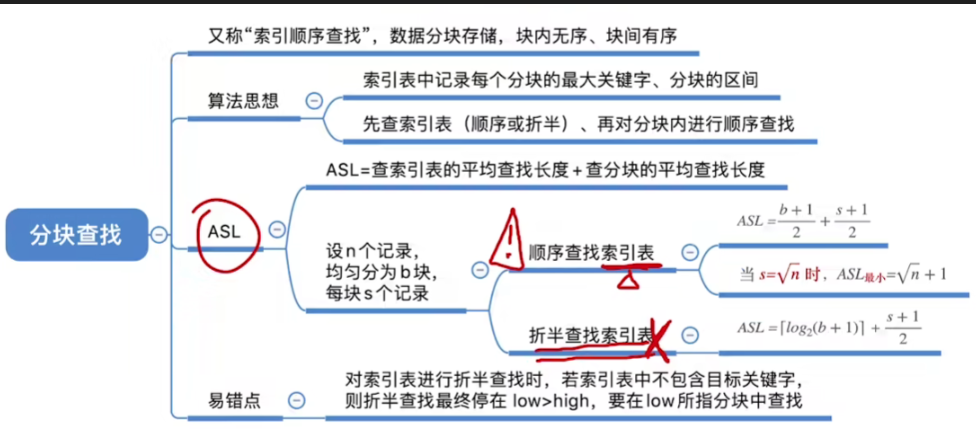
六.拓展思考
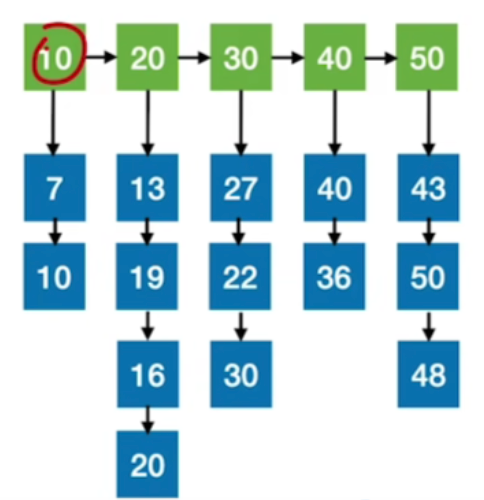
- 若查找表是"动态查找表",有没有更好的实现方式?
答:现在如果这个查找表当中,经常需要进行元素的啊增加或者删除,比如现在我想要增加一个元素,这个元素的值是8,因为我们必须保证块间是有序的,所以如果我们要插入8这个数据,那我们只能在第一个分块内找一个位置插入.
那就会导致我们需要把后面的所有元素全部后移一位,就会浪费大量的时间
那么,解决方式就是链式存储,时间复杂度会显著降低
结语
一更😉
如果想查看更多章节,请点击:一、数据结构专栏导航页