235. Lowest Common Ancestor of a Binary Search Tree

Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.

According to the definition of LCA on Wikipedia: "The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself)."

Example 1:

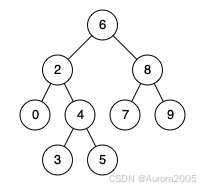
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.

Example 2:

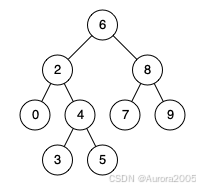
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.

Example 3:

Input: root = [2,1], p = 2, q = 1
Output: 2

Constraints:

• The number of nodes in the tree is in the range [2, 105].
• -109 <= Node.val <= 109
• All Node.val are unique.
• p != q
• p and q will exist in the BST.

递归法：

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root->val>p->val && root->val>q->val){
            return lowestCommonAncestor(root->left,p,q);
        }
        else if(root->val<p->val && root->val<q->val){
            return lowestCommonAncestor(root->right,p,q);
        }
        else return root;
    }
};

注意：

第一步，如果root->val比pq都要大就递归左子树，反之递归右子树

第二步，如果不是上面两种（root就是最近公共祖先）就返回root

迭代：

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        while(root){
            if(root->val>p->val && root->val>q->val)root=root->left;
            else if(root->val<p->val && root->val<q->val)root=root->right;
            else return root;
        }
        return NULL;
    }
};

注意：

不要忘记最后一行的return NULL，又是被这么简短的迭代感动哭的一天