模型汇总
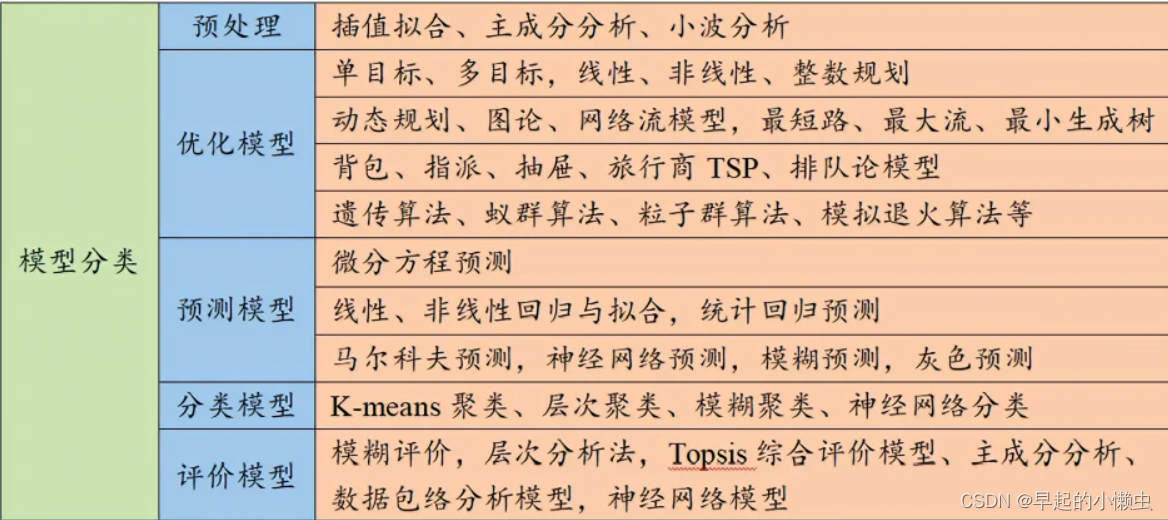
数据分析
数据处理
用Python进行数据挖掘(数据预处理)
Python机器学习库SKLearn:数据预处理
在Python中进行数据清洗和预处理缺失值处理缺失值补全
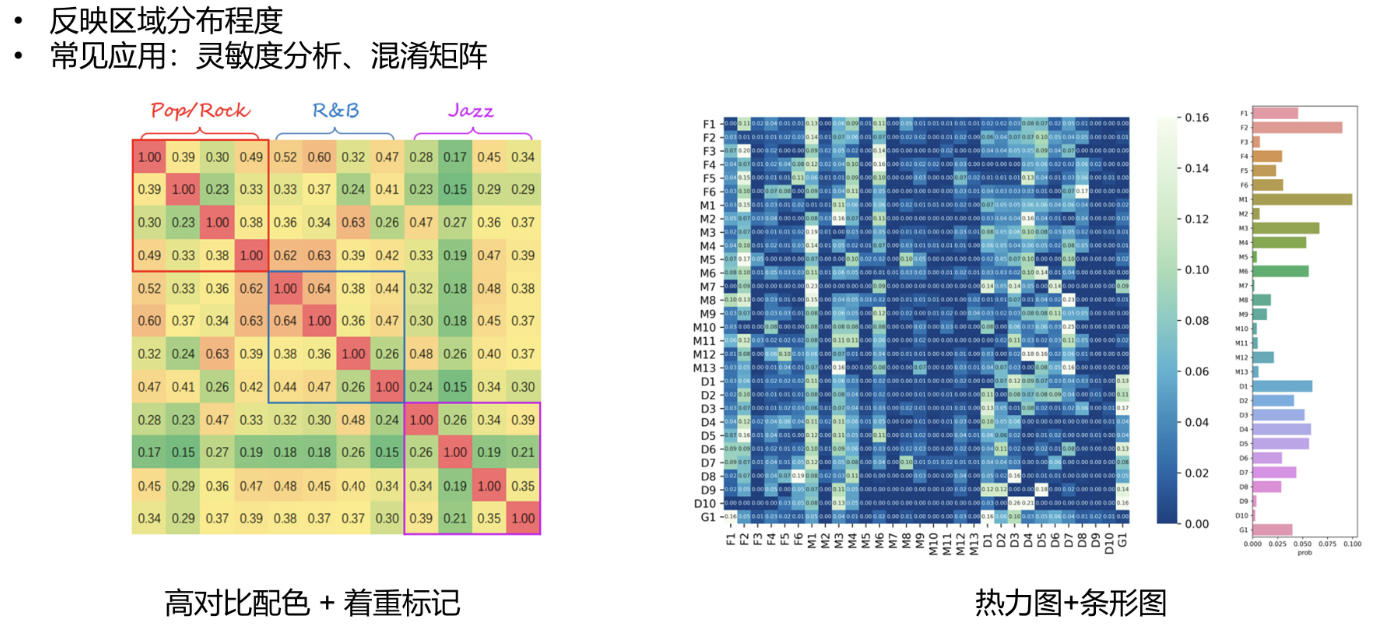
灵敏度分析
研究与分析一个系统(或模型)的状态或输出变化对系统参数或周围条件变化的敏感程度的方法。它通过改变模型中的一个或多个输入参数,观察输出结果的变化情况,来评估模型对于输入参数的敏感性。
一般用在线性规划模型 。
深入理解灵敏度分析与鲁棒性分析:技术实践与应用
绘图
【数学建模绘图系列教程】:一、图表类型和工具选择
使用matplotlib绘制柱状图
热力图
用 seaborn 绘制
相关性矩阵
模型评价
python
from pulp import *
# 创建一个线性规划问题
prob = LpProblem("Maximize_Profit", LpMaximize)
# 定义决策变量
x = LpVariable.dicts("Area", [(i, j) for i in range(num_fields) for j in range(num_crops)], 0, None)
y = LpVariable.dicts("Area_Greenhouse", [(k, l) for k in range(num_greenhouses) for l in range(num_crops)], 0, None)
# 定义目标函数
profit = lpSum([prices[j] * yields[j] * x[i, j] for i in range(num_fields) for j in range(num_crops)])
profit += lpSum([prices[l] * yields[l] * y[k, l] for k in range(num_greenhouses) for l in range(num_crops)])
prob += profit
# 添加约束条件
for i in range(num_fields):
prob += lpSum([x[i, j] for j in range(num_crops)]) <= field_areas[i]
for k in range(num_greenhouses):
prob += lpSum([y[k, l] for l in range(num_crops)]) <= greenhouse_area
# 求解模型
prob.solve()
# 打印结果
for v in prob.variables():
print(f"{v.name} = {v.varValue}")
print(f"Total Profit = {value(prob.objective)}")
python
from pulp import *
import numpy as np
# 创建线性规划问题
prob = LpProblem("Maximize_Profit", LpMaximize)
# 定义参数(示例)
fields = range(34)
crops = range(10) # 假设有10种作物
greenhouses = range(16)
years = range(2024, 2031)
# 假设的数据
areas = {i: 1201/34 for i in fields} # 每个地块的面积
prices = {j: 10 + 0.5 * j for j in crops} # 作物价格(示例)
yields = {j: 2 + 0.1 * j for j in crops} # 作物亩产量(示例)
costs = {j: 5 + 0.3 * j for j in crops} # 作物种植成本(示例)
# 定义决策变量
x = LpVariable.dicts("Area_Field", [(i, j, t) for i in fields for j in crops for t in years], 0, None)
y = LpVariable.dicts("Area_Greenhouse", [(k, j, t) for k in greenhouses for j in crops for t in years], 0, None)
# 目标函数
profit = lpSum([prices[j] * yields[j] * x[i, j, t] - costs[j] * x[i, j, t] for i in fields for j in crops for t in years])
profit += lpSum([prices[j] * yields[j] * y[k, j, t] - costs[j] * y[k, j, t] for k in greenhouses for j in crops for t in years])
prob += profit
# 添加约束条件
for i in fields:
for t in years:
prob += lpSum([x[i, j, t] for j in crops]) <= areas[i]
for k in greenhouses:
for t in years:
prob += lpSum([y[k, j, t] for j in crops]) <= 0.6 # 每个大棚的面积为0.6亩
# 求解模型
prob.solve()
# 打印结果
for v in prob.variables():
print(f"{v.name} = {v.varValue}")
print(f"Total Profit = {value(prob.objective)}")