尝试一个简单的卡尔曼滤波

萌发了找个简单例子帮助自己理解的想法，卡尔曼的作用在于可以在任何含有不确定信息 的动态系统中使用滤波，对系统下一步的走向做出有根据的预测，即使伴随着各种干扰，卡尔曼滤波总是能指出真实发生的情况。

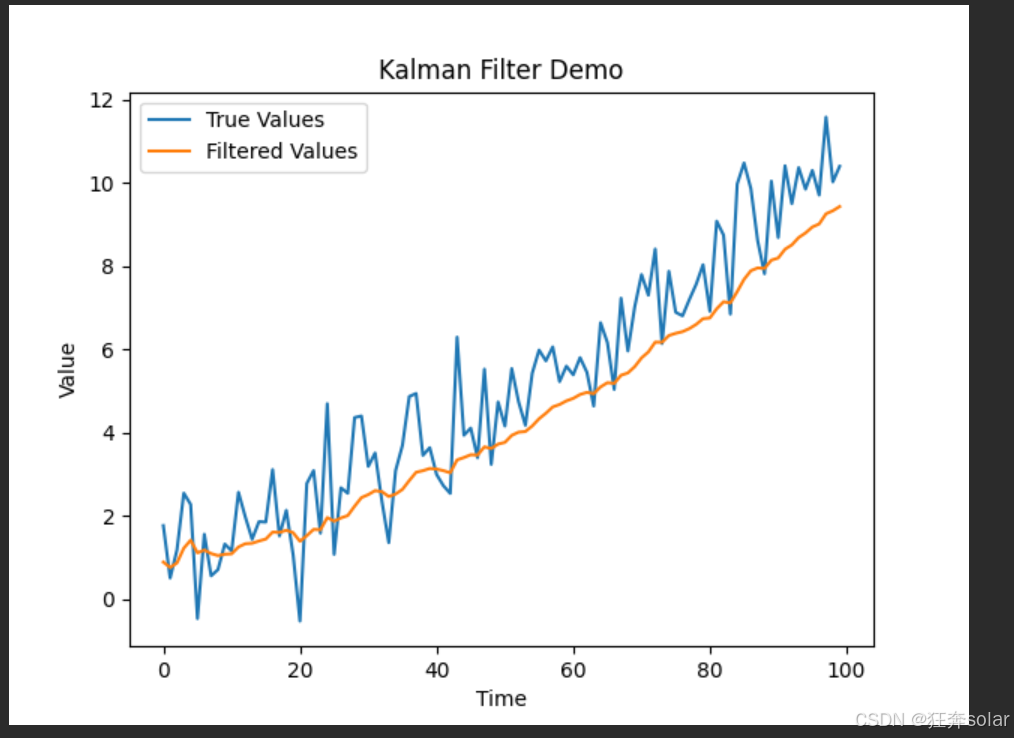
用一个线性随机波动的真实序列做卡尔曼滤波测试

import numpy as np
import matplotlib.pyplot as plt

# 定义卡尔曼滤波器
class KalmanFilter:
    def __init__(self, process_variance, measurement_variance, estimated_measurement_variance):
        self.process_variance = process_variance
        self.measurement_variance = measurement_variance
        self.estimated_measurement_variance = estimated_measurement_variance
        self.posteri_estimate = 0.0
        self.posteri_error_estimate = 1.0

    def update(self, measurement):
        # 预测步骤
        priori_estimate = self.posteri_estimate
        priori_error_estimate = self.posteri_error_estimate + self.process_variance

        # 更新步骤
        blending_factor = priori_error_estimate / (priori_error_estimate + self.measurement_variance)
        self.posteri_estimate = priori_estimate + blending_factor * (measurement - priori_estimate)
        self.posteri_error_estimate = (1 - blending_factor) * priori_error_estimate

        return self.posteri_estimate

# 模拟观测数据
np.random.seed(0)
true_values = np.linspace(0, 10, 100) + np.random.normal(0, 1, 100)

# 初始化滤波器
kf = KalmanFilter(process_variance=0.01, measurement_variance=1, estimated_measurement_variance=0.01)

# 对观测数据进行滤波
filtered_values = []
for measurement in true_values:
    filtered_values.append(kf.update(measurement))

# 绘制结果
plt.plot(range(100), true_values, label='True Values')
plt.plot(range(100), filtered_values, label='Filtered Values')
plt.xlabel('Time')
plt.ylabel('Value')
plt.title('Kalman Filter Demo')
plt.legend()
plt.show()

类的构造函数，用于初始化卡尔曼滤波器的参数。

process_variance：过程噪声的方差，表示系统自身的变化不确定性。
measurement_variance：测量噪声的方差，表示测量值的不确定性。
estimated_measurement_variance：预估的测量方差（在这个代码中未使用）。
posteri_estimate：后验估计值，初始化为 0.0，表示当前对系统状态的估计。
posteri_error_estimate：后验误差估计，初始化为 1.0，表示当前估计的误差。

update 方法：用于更新卡尔曼滤波器的状态。

measurement：当前测量值。
预测步骤 ：
- priori_estimate：当前的后验估计值，即上一次更新后的估计。
- priori_error_estimate：预测的误差估计，通过将后验误差加上过程噪声来获得。

更新步骤：

blending_factor：混合因子，决定了预测值和测量值在最终估计中的权重。它的值在 0 到 1 之间，越接近 1 表示测量值越可信，越接近 0 表示预测值越可信。
self.posteri_estimate：更新后的后验估计值，通过将预测值与当前测量值结合来计算。
self.posteri_error_estimate：更新后的后验误差估计，反映了新的误差情况。

最后，该方法返回更新后的后验估计值，表示当前对系统状态的最新估计。

整体来说，KalmanFilter 类实现了卡尔曼滤波的基本逻辑，能够根据不断更新的测量值来优化对系统状态的估计。通过预测和更新步骤，它有效地结合了测量噪声和过程噪声，从而提供一个更准确的状态估计。

测试结果