软间隔支持向量
这一节我们要回答的问题是?如何判断一个点是软间隔支持向量机中的支持向量,在硬间隔支持向量机中,支持向量只需要满足一个等式:
y i ( w T x i + b ) − 1 = 0 y_i(w^Tx_i + b) -1 =0 yi(wTxi+b)−1=0
在软间隔支持向量机中支持向量的定义并没有改变,依旧是距离超平面 1 ∥ ω ∥ \frac{1}{\Vert \omega \Vert} ∥ω∥1的点,但是因为引入的了松弛变量 ζ i \zeta_i ζi,所以我们需要对每一个点进行判断,这里我们判断的依据是KKT条件。
原始可行性: y i ( w T x i + b ) ≥ 1 − ζ i 对偶可行性: α i ≥ 0 μ i ≥ 0 互补松弛条件: α i ( y i ( w T x i + b ) − 1 + ξ i ) = 0 μ i ζ i = 0 C − α i − μ i = 0 原始可行性:y_i(w^Tx_i + b) \geq 1-\zeta_i\\ 对偶可行性:\alpha_i \geq 0 \quad \mu_i \geq 0\\ 互补松弛条件:\alpha_{i}(y_i(w^Tx_i + b) - 1 + \xi_i) = 0 \\\mu_i\zeta_i = 0 \\C -\alpha_i- \mu_i = 0 原始可行性:yi(wTxi+b)≥1−ζi对偶可行性:αi≥0μi≥0互补松弛条件:αi(yi(wTxi+b)−1+ξi)=0μiζi=0C−αi−μi=0
Case1: IF α = 0 \alpha =0 α=0 此时意味着 α i ( y i ( w T x i + b ) − 1 + ξ i ) = 0 \alpha_{i}(y_i(w^Tx_i + b) - 1 + \xi_i) = 0 αi(yi(wTxi+b)−1+ξi)=0恒成立,因为松弛变量 ζ ≥ 0 \zeta \geq 0 ζ≥0,且约束 y i ( w T x i + b ) ≥ 1 − ζ i y_i(w^Tx_i + b) \geq 1-\zeta_i yi(wTxi+b)≥1−ζi,则左边大于右边的最大值也就是: y i ( w T x i + b ) ≥ 1 y_i(w^Tx_i + b) \geq 1 yi(wTxi+b)≥1,此时就代表样本在间隔边界上或者已经被正确分类,对决策边界没有影响,如图中case1点。
Case2: IF 0 < α i < C 0 < \alpha_i < C 0<αi<C,当 0 < α i < C 0 < \alpha_i < C 0<αi<C时,由 C − α i − μ i = 0 C - \alpha_i - \mu_i = 0 C−αi−μi=0可得 μ i > 0 \mu_i > 0 μi>0,因为 μ i ( ξ i ) = 0 \mu_i(\xi_i) = 0 μi(ξi)=0(互补松弛条件),所以 ξ i = 0 \xi_i = 0 ξi=0。又因为 α i ( y i ( w ⋅ x i + b ) − 1 + ξ i ) = 0 \alpha_i(y_i(w \cdot x_i + b) - 1 + \xi_i) = 0 αi(yi(w⋅xi+b)−1+ξi)=0且 ξ i = 0 \xi_i = 0 ξi=0,所以 y i ( w ⋅ x i + b ) = 1 y_i(w \cdot x_i + b) = 1 yi(w⋅xi+b)=1。这表明样本点 x i x_i xi位于间隔边界上,是支持向量,对决策边界有影响。如图中点Case2点
Case3:IF α = C \alpha =C α=C,当 α i = C \alpha_i = C αi=C时,由 C − α i − μ i = 0 C - \alpha_i - \mu_i = 0 C−αi−μi=0可得 μ i = 0 \mu_i = 0 μi=0,因为 α i ( y i ( w ⋅ x i + b ) − 1 + ξ i ) = 0 \alpha_i(y_i(w \cdot x_i + b) - 1+\xi_i) = 0 αi(yi(w⋅xi+b)−1+ξi)=0且 α i = C > 0 \alpha_i = C > 0 αi=C>0,所以 y i ( w ⋅ x i + b ) − 1 + ξ i = 0 y_i(w \cdot x_i + b) - 1+\xi_i = 0 yi(w⋅xi+b)−1+ξi=0,即 ξ i = 1 − y i ( w ⋅ x i + b ) \xi_i = 1 - y_i(w \cdot x_i + b) ξi=1−yi(w⋅xi+b)。由于 ξ i ≥ 0 \xi_i \geq 0 ξi≥0,所以 y i ( w ⋅ x i + b ) ≤ 1 y_i(w \cdot x_i + b) \leq 1 yi(w⋅xi+b)≤1。这意味着样本点 x i x_i xi可能在间隔内部或者违反间隔边界,有可能是异常点或者对决策边界有较大影响的点。
当 ζ i = 0 时 \zeta_i=0时 ζi=0时, y i ( w ⋅ x i + b ) = 1 y_i(w \cdot x_i + b)=1 yi(w⋅xi+b)=1,样本点位于间隔边界上,是支持向量。
当 0 < ζ i < 1 0<\zeta_i<1 0<ζi<1时,由 ξ i = 1 − y i ( w T x i + b ) \xi_{i} = 1 - y_{i}(w^{T}x_{i}+b) ξi=1−yi(wTxi+b),可得 0 < 1 − y i ( w T x i + b ) < 1 0 < 1 - y_{i}(w^{T}x_{i}+b) < 1 0<1−yi(wTxi+b)<1,即 0 < y i ( w T x i + b ) < 1 0 < y_{i}(w^{T}x_{i}+b) < 1 0<yi(wTxi+b)<1。这意味着样本点 x i x_{i} xi 在间隔内部,但靠近间隔边界。如图中点Case3。
当 ζ i ≥ 1 \zeta_i\geq1 ζi≥1时,可得 1 − y i ( w T x i + b ) ≥ 1 1 - y_{i}(w^{T}x_{i}+b) \geq 1 1−yi(wTxi+b)≥1,即 y i ( w T x i + b ) < 0 y_{i}(w^{T}x_{i}+b) < 0 yi(wTxi+b)<0,此时点在错误的类别区域,可能在负支持向量超平面与超平面的间隔之间,或者直接越过了负支持向量超平面。如图中点Case4,5。
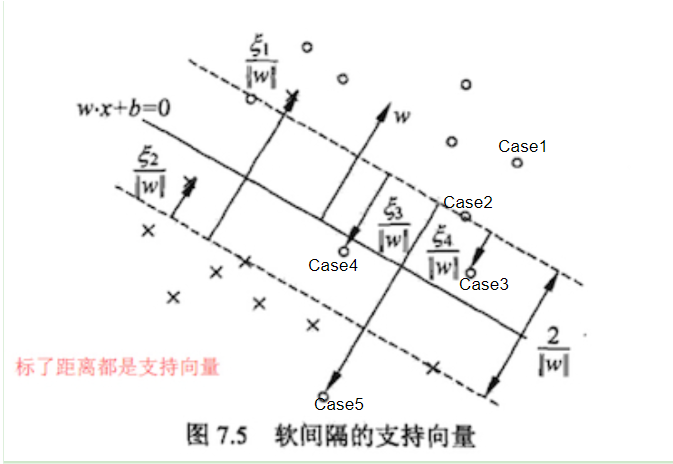
综上如果从松弛变量的值角度来看,当 ζ i = 0 \zeta_i =0 ζi=0时,点要么已经分类好,要么是支持向量,当 0 < ζ < 1 0<\zeta<1 0<ζ<1时,点分类的没问题,但是越过了支持向量平面,当 ζ ≥ 1 \zeta \geq 1 ζ≥1时点没有被分类好,可能在超平面上,可能越过了超平面或者反方向的支持向量平面