机器学习 PPT 内容总结
一、K 均值算法（k-means）PPT 总结
（一）聚类算法基础
- 核心概念：聚类是无监督学习问题，核心是将相似数据归为一组，关键难点在于聚类结果的评估与参数调优。
- 距离度量：是判断数据相似性的核心依据，主要有两种常用方式：
欧式距离：衡量多维空间中两点的绝对距离，适用于常规连续数据。
二维空间：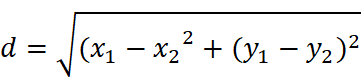
三维空间：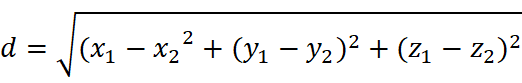
n 维空间：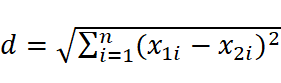
曼哈顿距离 ：也称出租车几何距离，计算两点在标准坐标系上的绝对轴距总和，适用于注重坐标轴方向差异的场景，平面空间公式为：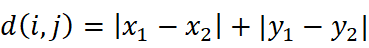
。
（二）K 均值算法核心内容
- 算法步骤（迭代优化过程）
- 初始化：设迭代次数(t=0)，随机选择(k)个样本作为初始聚类中心\m(t)。
- 样本聚类：固定聚类中心，计算每个样本到各中心的距离，将样本指派到最近中心所属的类，形成聚类结果C(t)。
- 更新中心：基于聚类结果C(t)，计算每个类内所有样本的均值，作为新的聚类中心m(t+1)。
- 迭代停止：若迭代收敛（中心变化极小）或满足停止条件，输出最终聚类结果C^*=C(t)；否则t=t+1，返回步骤 2。
- 算法评估（CH 指标）
评估逻辑：通过 "类内紧密度" 和 "类间分离度" 综合判断聚类效果。
计算依据：类内紧密度用 "类内各点与类中心的距离平方和" 衡量；类间分离度用 "各类中心点与数据集总中心的距离平方和" 衡量。
结果解读：CH 值越大，代表类内数据越紧密、类间差异越显著，聚类效果越优。
- 优缺点
优点：原理简单、运算速度快，适用于常规结构化数据集。
缺点：k值（聚类数量）需手动设定，难以确定最优值；算法复杂度与样本数量呈线性关系，处理超大规模数据时效率下降；仅能识别球形簇，无法发现任意形状的簇。
（三）代码实现相关
- 数据集生成（make_blobs 函数）：用于生成模拟聚类数据集，关键参数如下表：
|--------------|---------------------|---------------|
| 参数 | 说明 | 默认值 |
| n_samples | 数据样本点个数 | 100 |
| n_features | 每个样本的特征数（数据维度） | 2 |
| centers | 类别数（聚类目标数量） | 3 |
| cluster_std | 每个类别的数据方差（控制类内离散程度） | 无默认，需手动指定 |
| center_box | 聚类中心的取值范围 | (-10.0, 10.0) |
| shuffle | 是否打乱数据 | True |
| random_state | 随机种子（固定后可复现相同数据集） | 无 |
- K 均值聚类（KMeans 函数）：核心参数包括：
n_clusters：聚类簇的数量（即k值），需手动指定。
max_iter：最大迭代次数，防止迭代无限循环。
n_init：算法运行次数，取多次结果的最优值。
random_state：随机种子，确保结果可复现。
- 课堂练习：使用 make_blobs 函数生成自定义数据集，再通过 KMeans 函数实现聚类。
二、集成算法 PPT 总结
（一）集成学习基础
- 核心思想：借鉴 "多个专家共同决策优于单个专家" 的逻辑，通过构建并融合多个 "个体学习器"，提升模型的泛化能力（降低过拟合、提高准确性）。
- 定义：集成学习（ensemble learning）是通过组合多个个体学习器（如决策树、KNN 等）完成学习任务的框架，核心在于 "个体学习器生成" 与 "结果融合" 两个环节。
- 结合策略（个体学习器结果的融合方式）
简单平均法：对回归任务，直接计算所有个体学习器预测结果的平均值作为最终输出。
加权平均法：对回归 / 分类任务，根据个体学习器的性能（如准确率）分配不同权重，加权求和得到最终结果（性能越好，权重越高）。
投票法：对分类任务，采用 "少数服从多数" 原则，统计所有个体学习器的预测类别，得票最多的类别为最终结果。
投票法效果差异：当个体学习器误差独立时，集成可提升性能；若误差高度相关，集成可能无效甚至起负作用。
（二）集成算法分类及核心算法
根据个体学习器的生成方式，集成算法分为三类，具体如下：
|----------|----------------------------------------------|----------------------------|
| 类别 | 核心特点 | 代表算法 |
| Bagging | 个体学习器无强依赖，可并行生成；通过 "有放回采样"（bootstrap）构建不同训练集 | 随机森林 |
| Boosting | 个体学习器存在强依赖，需串行生成；通过 "加权调整" 优化样本与学习器权重 | AdaBoost |
| Stacking | 分阶段融合多种学习器；第一阶段用不同学习器预测，第二阶段用第一阶段结果训练 "元学习器" | 无特定代表，需自定义组合（如 KNN+SVM+RF） |
1. Bagging 与随机森林
Bagging 原理
全称：Bootstrap Aggregation（自助聚合）。
流程：通过有放回采样生成多个不同的训练集，并行训练多个个体学习器，最终用 "投票法"（分类）或 "简单平均法"（回归）融合结果。
公式（回归任务）：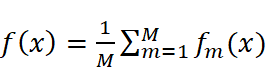
(M为个体学习器数量，(fm 
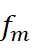(x)为第m个学习器的预测结果）。
随机森林（Bagging 的典型应用）
核心特点："随机"+"森林"。
随机：数据采样随机（有放回采样）、特征选择随机（每个决策树仅用部分特征训练）。
森林：由多个并行训练的决策树组成，无依赖关系。
构造逻辑：通过 "二重随机性" 确保每个决策树的差异性，避免单个决策树过拟合，最终通过投票法输出结果。
优势：
- 可处理高维度数据，无需手动进行特征选择。
- 训练后可输出特征重要性，便于特征分析。
- 个体学习器可并行训练，速度快。
- 决策树结构可可视化，便于模型解释。
- 关键函数及参数：
分类任务：RandomForestClassifier ()；回归任务：RandomForestRegressor ()。
核心参数如下表：
|--------------|----------------------------------|----------------|
| 参数 | 说明 | 默认值 |
| n_estimators | 决策树的数量（"森林" 的规模） | 100 |
| oob_score | 是否用 "袋外样本"（未被采样到的样本）评估模型，等同于交叉验证 | False |
| bootstrap | 是否采用有放回采样 | True |
| max_samples | 每个决策树训练用的最大样本量 | None（使用全部采样样本） |
课堂练习：使用 sklearn 的 load_wine（红酒数据集），通过随机森林算法实现葡萄酒分类（数据集含 13 个特征，3 个类别）。
2. Boosting 与 AdaBoost
Boosting 原理：从 "弱学习器"（性能略优于随机猜测的模型）开始，通过迭代调整样本权重与学习器权重，逐步提升模型性能，最终融合为 "强学习器"。
AdaBoost（Boosting 的典型应用）
核心逻辑："知错就改"，通过权重调整优化模型。
算法步骤：
- 初始化：给所有训练样本分配相同的初始权重。
- 训练弱学习器：基于当前样本权重训练模型，若样本分类错误，下一轮迭代中增加其权重；若分类正确，降低其权重。
- 迭代训练：用更新权重后的样本集训练下一个弱学习器，重复步骤 2。
- 融合强学习器：根据每个弱学习器的分类误差率分配权重（误差率越低，权重越高），将所有弱学习器加权组合为强学习器。
3. Stacking（堆叠）
核心特点："暴力融合 + 分阶段训练"，可组合任意类型的个体学习器（如 KNN、SVM、随机森林等）。
算法流程：
-
第一阶段（基础学习器训练）：用原始数据训练多个不同的基础学习器，得到各自的预测结果。
-
第二阶段（元学习器训练）：将第一阶段的预测结果作为 "新特征"，训练一个 "元学习器"（如逻辑回归、决策树），最终由元学习器输出最终预测结果。
导入make_blobs函数，用于生成样本数据
from sklearn.datasets import make_blobs
导入matplotlib库中的pyplot模块，用于绘图
import matplotlib.pyplot as plt
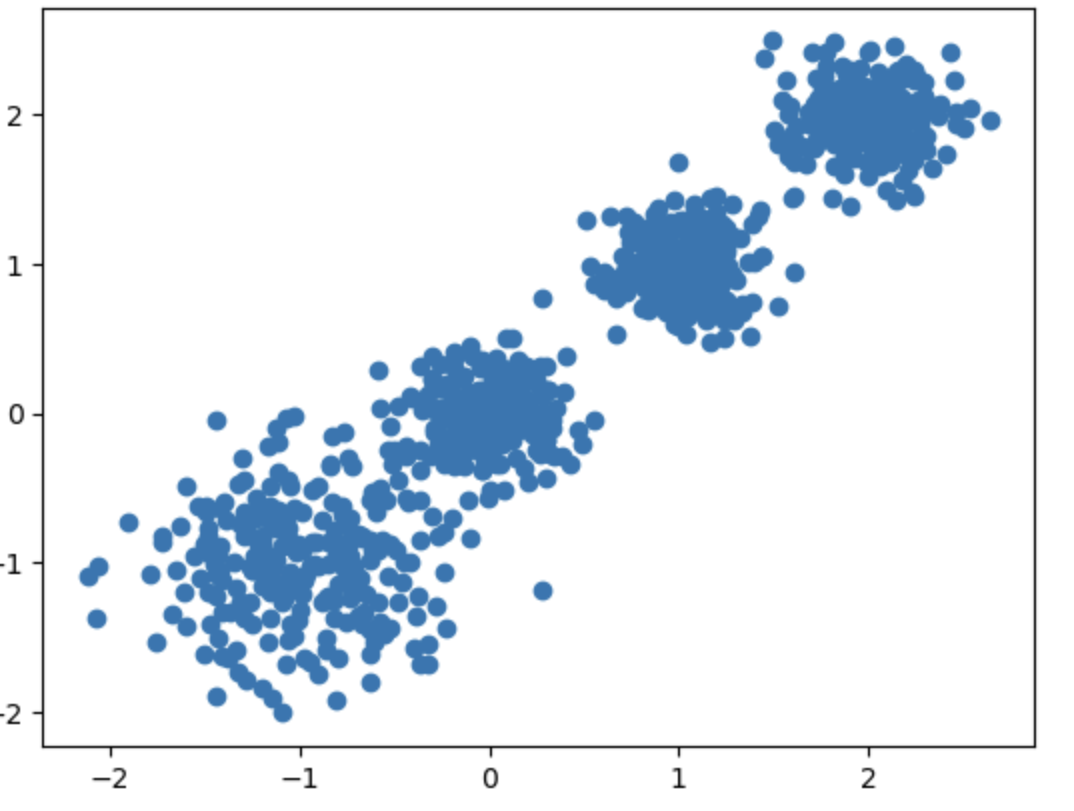
使用make_blobs生成样本数据
n_samples=1000表示生成1000个样本点
n_features=2表示每个样本点有2个特征
centers=[[-1,-1],[0,0],[1,1],[2,2]]定义了4个中心点，即4个聚类中心
cluster_std=[0.4, 0.2, 0.2, 0.2]定义了每个聚类中心的标准差，即数据点围绕中心点的分散程度
random_state=9用于设置随机种子，确保每次生成的数据相同
x, y = make_blobs(n_samples=1000, n_features=2,
centers=[[-1,-1], [0, 0], [1, 1], [2, 2]],
cluster_std=[0.4, 0.2, 0.2, 0.2],
random_state=9)使用matplotlib的scatter函数绘制散点图
x[:, 0]表示所有样本点的第一个特征，x[:, 1]表示所有样本点的第二个特征
marker="o"表示使用圆形标记来绘制点
plt.scatter(x[:, 0], x[:, 1], marker="o")
显示绘制的图形
plt.show()
导入KMeans类，用于执行K-Means聚类算法
from sklearn.cluster import KMeans
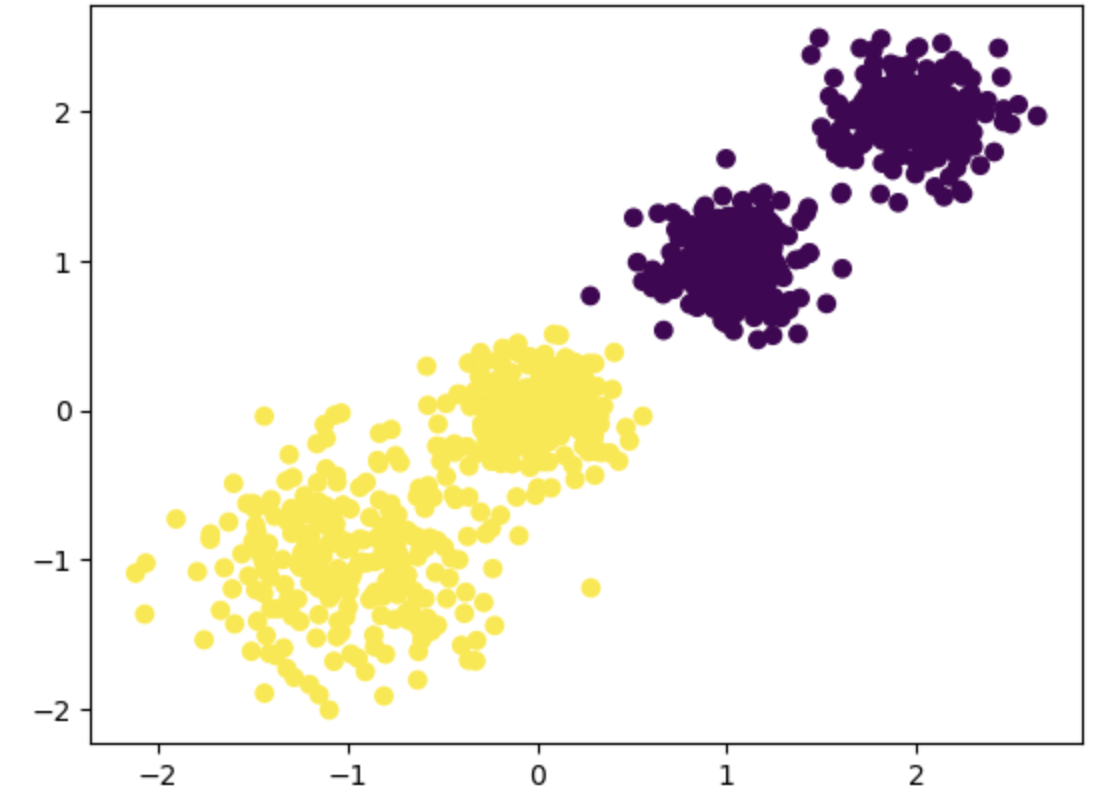
创建KMeans对象，设置聚类数为2，随机种子为9
fit_predict方法用于对数据进行聚类，并返回每个样本的聚类标签
y_pred = KMeans(n_clusters=2, random_state=9).fit_predict(x)
使用matplotlib的scatter函数绘制散点图
x[:, 0]表示所有样本点的第一个特征，x[:, 1]表示所有样本点的第二个特征
c=y_pred表示根据聚类标签对点进行着色，不同的颜色代表不同的聚类
plt.scatter(x[:, 0], x[:, 1], c=y_pred)
显示绘制的图形
plt.show()
