a 生成数据集,数据由 Y = X β + ϵ Y=X\beta+\epsilon Y=Xβ+ϵ产生,其中 p = 20 , n = 1000 p=20,n=1000 p=20,n=1000
{r}
#way1
set.seed(1)
p = 20
n = 1000
x = matrix(rnorm(n*p), n, p)
B = rnorm(p)
B[3] = 0
B[4] = 0
B[9] = 0
B[19] = 0
B[10] = 0
eps = rnorm(p)
y = x %*% B + eps#%*%为矩阵乘法
{r}
#way2
set.seed(1)
a=rnorm(20*1000)
x=matrix(a,1000,20)
eps=rnorm(1000)
beta=c(1,1,0,0,5.5,2,5,0,4,0,1.5,11,10.5,3.3,2.8,0,9,0,2,6.6)
y=x%*%beta+eps#%*%为矩阵乘法其中部分元素为0。
b 划分数据为训练集和测试集
{r}
#way1
train = sample(seq(1000), 100, replace = FALSE)
y.train = y[train,]
y.test = y[-train,]
x.train = x[train,]
x.test = x[-train,]
{r}
#way2
train=sample(1:1000,100,rep=F)
test=(-train)c 训练集MSE分析
{r}
#way1
library(leaps)
regfit.full = regsubsets(y~., data=data.frame(x=x.train, y=y.train), nvmax=p)
val.errors = rep(NA, p)
x_cols = colnames(x, do.NULL=FALSE, prefix="x.")
for (i in 1:p) {
coefi = coef(regfit.full, id=i)
pred = as.matrix(x.train[, x_cols %in% names(coefi)]) %*% coefi[names(coefi) %in% x_cols]
val.errors[i] = mean((y.train - pred)^2)
}
plot(val.errors, ylab="Training MSE", pch=19, type="b")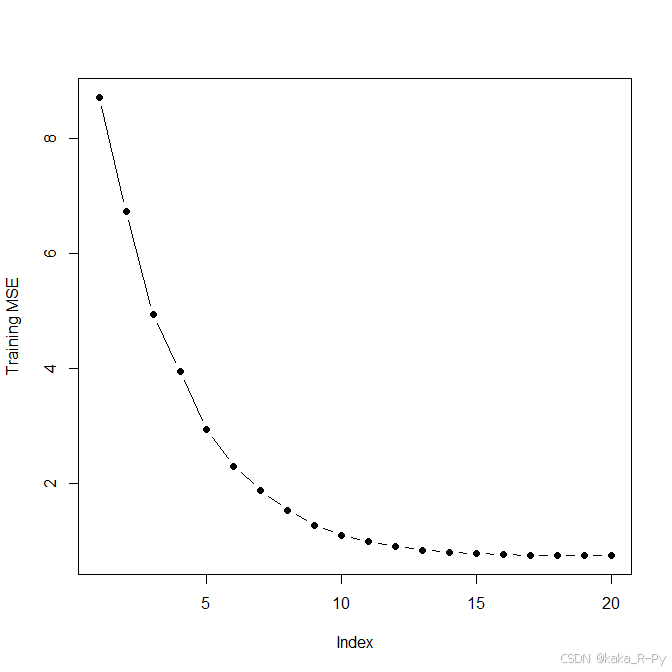
{r}
#way2
library(leaps)
d=data.frame(y,x)
fit1=regsubsets(y~.,data=d,subset=train,nvmax=20)
s1=summary(fit1)
mse=(s1$rss)/100
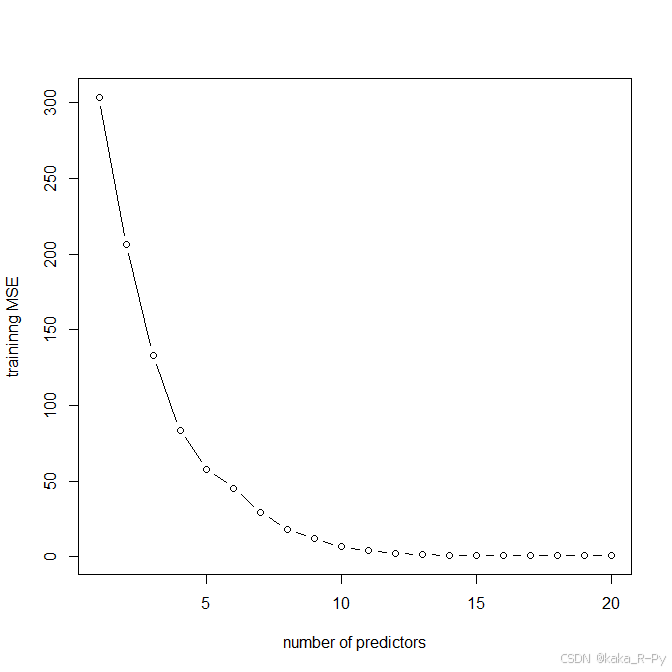
mse
which.min(mse)
plot(1:20,mse,type="b",xlab="number of predictors",ylab="traininng MSE")
{r}
> d=data.frame(y,x)
> fit1=regsubsets(y~.,data=d,subset=train,nvmax=20)
> s1=summary(fit1)
> s1
Subset selection object
Call: regsubsets.formula(y ~ ., data = d, subset = train, nvmax = 20)
20 Variables (and intercept)
Forced in Forced out
X1 FALSE FALSE
X2 FALSE FALSE
X3 FALSE FALSE
X4 FALSE FALSE
X5 FALSE FALSE
X6 FALSE FALSE
X7 FALSE FALSE
X8 FALSE FALSE
X9 FALSE FALSE
X10 FALSE FALSE
X11 FALSE FALSE
X12 FALSE FALSE
X13 FALSE FALSE
X14 FALSE FALSE
X15 FALSE FALSE
X16 FALSE FALSE
X17 FALSE FALSE
X18 FALSE FALSE
X19 FALSE FALSE
X20 FALSE FALSE
1 subsets of each size up to 20
Selection Algorithm: exhaustive
X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 X11 X12 X13 X14 X15 X16 X17 X18 X19 X20
1 ( 1 ) " " " " " " " " " " " " " " " " " " " " " " "*" " " " " " " " " " " " " " " " "
2 ( 1 ) " " " " " " " " " " " " " " " " " " " " " " "*" " " " " " " " " "*" " " " " " "
3 ( 1 ) " " " " " " " " " " " " " " " " " " " " " " "*" "*" " " " " " " "*" " " " " " "
4 ( 1 ) " " " " " " " " " " " " " " " " " " " " " " "*" "*" " " " " " " "*" " " " " "*"
5 ( 1 ) " " " " " " " " "*" " " " " " " " " " " " " "*" "*" " " " " " " "*" " " " " "*"
6 ( 1 ) " " " " " " " " "*" " " "*" " " " " " " " " "*" "*" " " " " " " "*" " " " " "*"
7 ( 1 ) " " " " " " " " "*" " " "*" " " "*" " " " " "*" "*" " " " " " " "*" " " " " "*"
8 ( 1 ) " " " " " " " " "*" " " "*" " " "*" " " " " "*" "*" "*" " " " " "*" " " " " "*"
9 ( 1 ) " " " " " " " " "*" " " "*" " " "*" " " " " "*" "*" "*" "*" " " "*" " " " " "*"
10 ( 1 ) " " " " " " " " "*" " " "*" " " "*" " " " " "*" "*" "*" "*" " " "*" " " "*" "*"
11 ( 1 ) " " " " " " " " "*" "*" "*" " " "*" " " " " "*" "*" "*" "*" " " "*" " " "*" "*"
12 ( 1 ) " " " " " " " " "*" "*" "*" " " "*" " " "*" "*" "*" "*" "*" " " "*" " " "*" "*"
13 ( 1 ) " " "*" " " " " "*" "*" "*" " " "*" " " "*" "*" "*" "*" "*" " " "*" " " "*" "*"
14 ( 1 ) "*" "*" " " " " "*" "*" "*" " " "*" " " "*" "*" "*" "*" "*" " " "*" " " "*" "*"
15 ( 1 ) "*" "*" " " " " "*" "*" "*" "*" "*" " " "*" "*" "*" "*" "*" " " "*" " " "*" "*"
16 ( 1 ) "*" "*" " " " " "*" "*" "*" "*" "*" " " "*" "*" "*" "*" "*" " " "*" "*" "*" "*"
17 ( 1 ) "*" "*" "*" " " "*" "*" "*" "*" "*" " " "*" "*" "*" "*" "*" " " "*" "*" "*" "*"
18 ( 1 ) "*" "*" "*" "*" "*" "*" "*" "*" "*" " " "*" "*" "*" "*" "*" " " "*" "*" "*" "*"
19 ( 1 ) "*" "*" " " "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*"
20 ( 1 ) "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*"
d 测试集MSE分析
{r}
#way1
val.errors = rep(NA, p)
for (i in 1:p) {
coefi = coef(regfit.full, id=i)
pred = as.matrix(x.test[, x_cols %in% names(coefi)]) %*% coefi[names(coefi) %in% x_cols]#测试集的Y
val.errors[i] = mean((y.test - pred)^2)#计算MSE
}
plot(val.errors, ylab="Test MSE", pch=19, type="b")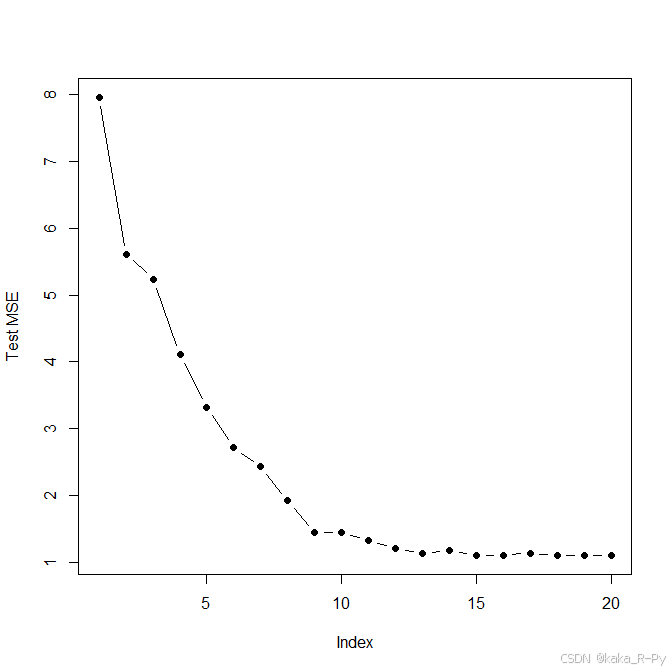
{r}
#way2
xmat=model.matrix(y~.,data=d)
mse1=rep(NA,20)
for(i in 1:20){
pred=xmat[test,][,names(coefficients(
fit1,id=i))]%*%coefficients(fit1,id=i)
mse1[i]=mean((pred-y[test])^2)
}
mse1
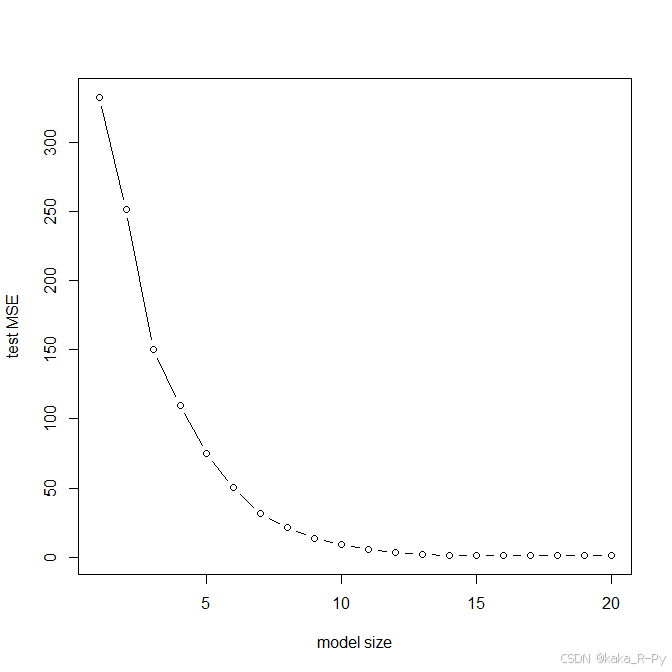
plot(1:20,mse1,type="b",xlab="model size",ylab="test MSE")

e 当模型含有多少个特征时,测试集MSE最小。
{r}
#way1
which.min(val.errors)16 parameter model has the smallest test MSE.
{r}
#way2
which.min(mse1)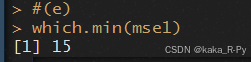
15 parameter model has the smallest test MSE.
f 测试集MSE最小的模型与真实模型比较起来有何不同,比较模型系数。
{r}
#way1
coef(regfit.full, id=16)
Caught all but one zeroed out coefficient at x.2,x.4,x.10,x.19.
{r}
#way2
coefficients(fit1,id=15)
Caught all but one zeroed out coefficient at x.3,x.4,x.8,x.10,x.16.
g 作出 r r r在一定范围内取值时 ∑ j = 1 p ( β j − β ^ j r ) 2 \sqrt{\sum_{j=1}^p\left(\beta_j-\hat{\beta}_j^r\right)^2} ∑j=1p(βj−β^jr)2 的图像,其中 β ^ j r \hat{\beta}_j^r β^jr为包含 r r r个预测变量的最优模型中第 j j j个系数的估计值。
{r}
#way1
val.errors = rep(NA, p)
a = rep(NA, p)
b = rep(NA, p)
for (i in 1:p) {
coefi = coef(regfit.full, id=i)
a[i] = length(coefi)-1
b[i] = sqrt(
sum((B[x_cols %in% names(coefi)] - coefi[names(coefi) %in% x_cols])^2) +
sum(B[!(x_cols %in% names(coefi))])^2)
}
plot(x=a, y=b, xlab="number of coefficients",
ylab="error between estimated and true coefficients")
which.min(b)

Model with 9 coefficients (10 with intercept) minimizes the error between the
estimated and true coefficients. Test error is minimized with 16 parameter model.
A better fit of true coefficients as measured here doesn't mean the model will have.
{r}
#way2
xcol=colnames(x,do.NULL =F,prefix = "X")
s=rep(NA,20)
for(i in 1:20){
s[i]=sqrt(sum(beta[xcol%in%names(coefficients(fit1,id=i)[-1])]-
coefficients(fit1,id=i)[-1])^2+
sum(beta[!xcol%in%names(coefficients(fit1,id=i)[-1])])^2)
}
plot(1:20,s,type="b",xlab="numbers of coeffieients",
ylab='error between estimated and true coefficients')
which.min(s)

Model with 15 coefficients (15 with intercept) minimizes the error between the
estimated and true coefficients. Test error is minimized with 15 parameter model.
A better fit of true coefficients as measured here doesn't mean the model will have.