2024 亚太地区数学建模竞赛
问题 C
宠物产业及相关产业的发展分析与策略
问题背景
随着人们消费理念的逐步发展,宠物行业作为新兴产业,凭借着经济的快速发展和人均收入的不断提高,逐渐在全球范围内积聚动能。1992年,中国小动物保护协会成立,1993年,皇家宠物食品(Royal Canin)和玛氏(Mars)等国际宠物品牌进入中国市场。与宠物相关的行业------如宠物食品、宠物诊所、宠物用品和宠物护理等,也因"宠物陪伴"在中国的流行而逐渐拥有了广阔且快速增长的市场。因此,分析宠物行业的发展趋势及市场需求,以及根据分析和当前的经济环境,为中国宠物行业的发展提出相应的战略建议至关重要。
**问题分析:**四个问题需要建立数学模型进行解决,包括预测中国的宠物行业发展情况、全球对宠物食品的需求以及全球宠物食品市场的需求趋势以及中国的发展情况,最后还需要为食品行业的可持续发展制定可行的策略。这些问题涉及数据爬虫收集、数据处理、统计分析、模型预测等多个数学建模技术。通过合理的数据处理和算法选择,可以为为宠物行业的可持续发展提出相应的战略建议。
问题1分析:分析过去五年中国宠物行业的发展趋势(按宠物种类:猫和狗),并构建数学模型预测未来三年发展。
问题1:基于附件1中的数据及您的团队收集的额外数据,请分析过去五年中国宠物行业按宠物类型(猫/狗)的发展情况。并分析中国宠物行业发展的影响因素,从而建立一个合适的数学模型,预测未来三年中国宠物行业的发展。
核心需求:
(1)数据分析(包括附件和自行收集的数据)。
【收集的数据】
1、社会经济数据
GDP增长率:作为宏观经济背景指标。
城市化率:城市化通常伴随宠物数量增长。
家庭结构:单身家庭或无子家庭比例对养宠意愿的影响。
2、政策和文化相关数据
政府关于宠物行业的支持政策或法规(如养宠物的税费、规定)。
宠物文化的推广事件或活动。
3、其他行业数据
宠物消费水平:宠物用品、宠物医疗开支等数据。
宠物行业就业人数:反映行业活跃程度。
4、外部因素数据
社交媒体或互联网搜索指数(反映宠物的流行程度)。
(2)提取关键因素(经济水平、宠物文化、政策等)。
(3)预测模型(例如时间序列分析、回归模型等)。
解题方法:
数据预处理:
(1)使用附件中中国猫狗数量数据,计算年增长率。
(2)根据自行收集的经济数据,探索增长驱动因素。
优势:时间序列方法无需额外自变量,能直接捕捉数据中的趋势和周期性。
模型选择:
(1)时间序列模型:如 ARIMA、指数平滑法预测未来三年宠物数量。
(2)回归模型:以经济数据(人均收入等)为自变量,宠物数量为因变量。
优势:可以量化社会经济因素对宠物数量的影响,结果更具有解释性。
(3)机器学习方法:
使用 决策树回归 或 随机森林,结合更多复杂因素(如城市化率、年龄结构)。
优势:适用于非线性关系,更灵活,但需要更多数据支持。
分析输出:
(1)图表展示猫狗数量的趋势。
(2)解释关键驱动因素的作用。
预测结果验证:
(1)模型拟合度:通过均方误差(MSE)、平均绝对误差(MAE)等指标评价模型性能。
1、数据分析与相关性研究
1.1 数据收集与准备
为了分析中国宠物行业的发展及其影响因素,我们收集了中国2019年至2023年的宠物行业相关数据。将附件1给出的数据进行可视化,了解数据的分布以及趋势,数据包括猫和狗的数量(单位为万只)。
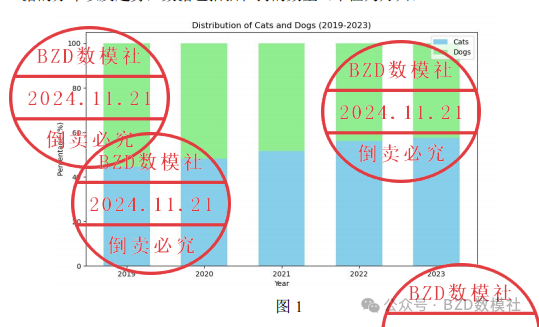
显然仅有上述数据是不够的,因此在一些网站上采集了其他可能影响宠物行业发展的社会经济因素,比如中国宠物食品总产值(人民币),中国宠物食品出口总值(美元),宠物市场规模(亿美元)等,数据收集完成后,我们对数据进行了清洗和整理,确保特征和目标变量无缺失或异常值。
1.2 相关性分析
为了找出与中国宠物行业发展最相关的影响因素,我们首先对各个特征与目标变量(即猫和狗的数量)进行了斯皮尔曼相关性分析。斯皮尔曼相关性是一种非参数检验方法,适用于分析数据之间的单调关系,特别适合存在非线性关系的数据。我们计算了所有特征与目标变量之间的斯皮尔曼相关系数,并以热力图的形式进行可视化,以更直观地展示各个因素的相关性。
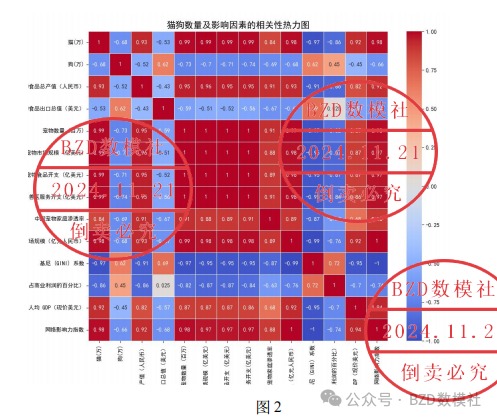
由于指标有很多,热力图不便于完全展示,这里仅仅选取了十几个指标进行观察,为了找到中国宠物行业发展的重要影响因素,这里建立随机森林模型分析特征重要性,以中国宠物猫狗数量为因变量分析,反映未来市场的变化趋势和潜在的增长空间,找到了影响最大的五个因素,如下表所示。
表1
|-----------------|-----------------|-----------------|
| Feature | Cats Importance | Dogs Importance |
| 总税率 (占商业利润的百分比) | 0.130597 | 0.181137 |
| 中国宠物食品总产值 (人民币) | 0.107714 | 0.124633 |
| 基尼 (GINI) 系数 | 0.101656 | 0.095881 |
| 宠物食品开支 (亿美元) | 0.094405 | 0.057406 |
| 农村人口 | 0.089761 | 0.072159 |
表2
|-----------------|-----------------|-----------------|
| Feature | Cats Importance | Dogs Importance |
| 总税率 (占商业利润的百分比) | 0.130597 | 0.181137 |
| 中国宠物食品总产值 (人民币) | 0.107714 | 0.124633 |
| 人均 GDP (现价美元) | 0.062375 | 0.102648 |
| 基尼 GINI) 系数 | 0.101656 | 0.095881 |
| 食品生产指数 | 0.084467 | 0.072211 |
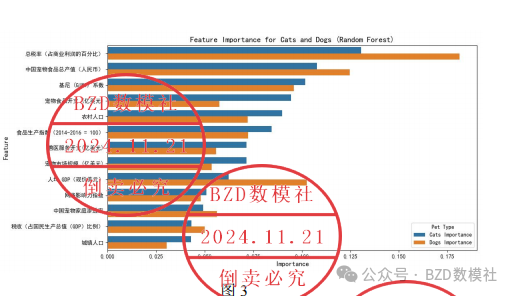
1、建立预测模型
为了预测未来三年(2024-2026年)中国宠物行业的发展情况,我们采用了三种不同的方法进行建模和预测:
(1)ARIMA 时间序列模型:用于捕捉数据的时间序列趋势和季节性特征。适合捕捉数据的时间序列特征,尤其是在数据具有明显趋势或季节性时。
(2)随机森林回归模型:一种基于集成学习的非线性模型,能够处理复杂的特征之间的交互。能够捕捉特征之间的复杂关系,预测结果对于非线性数据具有较高的精度。
(3)多元线性回归模型:用于分析各影响因素之间的线性关系,并进行未来趋势预测。能够提供各个特征对目标变量的线性解释,但对于非线性关系可能效果不佳。
2.1 ARIMA模型
ARIMA 模型需要输入平稳的时间序列数据,因此我们首先对猫和狗的数量进行了平稳性检测(ADF 检验),并对非平稳的数据进行差分处理直到其满足平稳性的要求。首先可以看到猫和狗的数据不是平稳的,因此不能直接采用ARIMA模型进行处理,所以要对数据进行差分操作,一阶差分之后,可以看到狗的数据是平稳的,但是猫的数据仍然是非平稳的,因此还要对猫的数据进行二阶差分处理。
Cats p-value (Diff): 0.42811060946796686
猫数据的一阶差分仍然非平稳
Dogs ADF Statistic (Diff): -6.142011812079186
Dogs p-value (Diff): 7.929541291227802e-08
狗数据的一阶差分是平稳的
在处理完毕之后,针对猫和狗的数据分别建立 ARIMA 模型,对未来三年进行预测。预测结果如下所示。
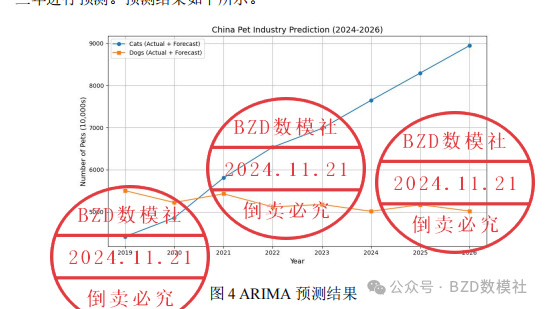
Cats Forecast (2024-2026): [7647.15363209 8295.50444178 8945.43956864]
Dogs Forecast (2024-2026): [5014.4923516 5169.36835894 5019.92639846]
Standard Deviation (Normalized) - Cats: 0.3778613945734487
Standard Deviation (Normalized) - Dogs: 0.38937160021701045
2.2 RandomForest模型
随机森林模型使用滞后特征来捕捉过去的数据对未来的影响,并使用随机森林模型进行特征选择,选择对目标变量最重要的特征。滞后特征工程 是通过使用滞后特征来增强特征矩阵。滞后特征用于捕捉时间序列数据中的时序依赖性,例如,未来的猫或狗数量很大程度上依赖于它们在过去几年的数量变化。特征选择 是用于优化模型性能的重要步骤。通过减少输入特征数量,可以降低模型的复杂度,从而提高模型的泛化能力。选择了前 10 个最重要的特征作为输入特征。这种特征选择方式帮助模型去除了对输出影响较小的特征,减少了噪声,提高了模型的训练和预测性能。这也可以看作是一种特征降维的方式,减少了模型的计算量,也使得模型更加健壮。
为了提高预测的准确率,还采用了留一法交叉验证。留一法交叉验证是一种交叉验证技术,其中数据集中的每一个样本依次作为验证集,其余的样本作为训练集。换句话说,如果数据集有 n 个样本,那么留一法交叉验证会执行 n 次训练,每次从 n-1 个样本中训练模型,然后使用剩余的一个样本进行测试。留一法的最大优势是充分利用了所有数据样本。在每次迭代中,模型都是用 n-1 个样本进行训练,只保留一个样本用于验证。这意味着模型基本上是在几乎所有数据上进行训练,因此能够较好地捕捉数据中的模式和规律,特别是在数据集很小的情况下,这种方法显得尤为重要。留一法交叉验证避免了在划分训练集和验证集时可能引入的偏差。在常规的 K 折交叉验证 中,训练集和测试集的划分可能会导致一些样本的代表性不足,从而引入额外的偏差。而留一法每次只使用一个样本作为验证集,确保每一个样本都被用来测试模型的性能,最终计算的平均误差更具有普遍性。