题目:
https://www.luogu.com.cn/problem/B3637
最长上升子序列
题目描述
这是一个简单的动规板子题。
给出一个由 n(n\\le 5000) 个不超过 10\^6 的正整数组成的序列。请输出这个序列的**最长上升子序列**的长度。
最长上升子序列是指,从原序列中**按顺序**取出一些数字排在一起,这些数字是**逐渐增大**的。
输入格式
第一行,一个整数 n,表示序列长度。
第二行有 n 个整数,表示这个序列。
输出格式
一个整数表示答案。
样例 #1
样例输入 #1
```
6
1 2 4 1 3 4
```
样例输出 #1
```
4
```
提示
分别取出 1、2、3、4 即可。
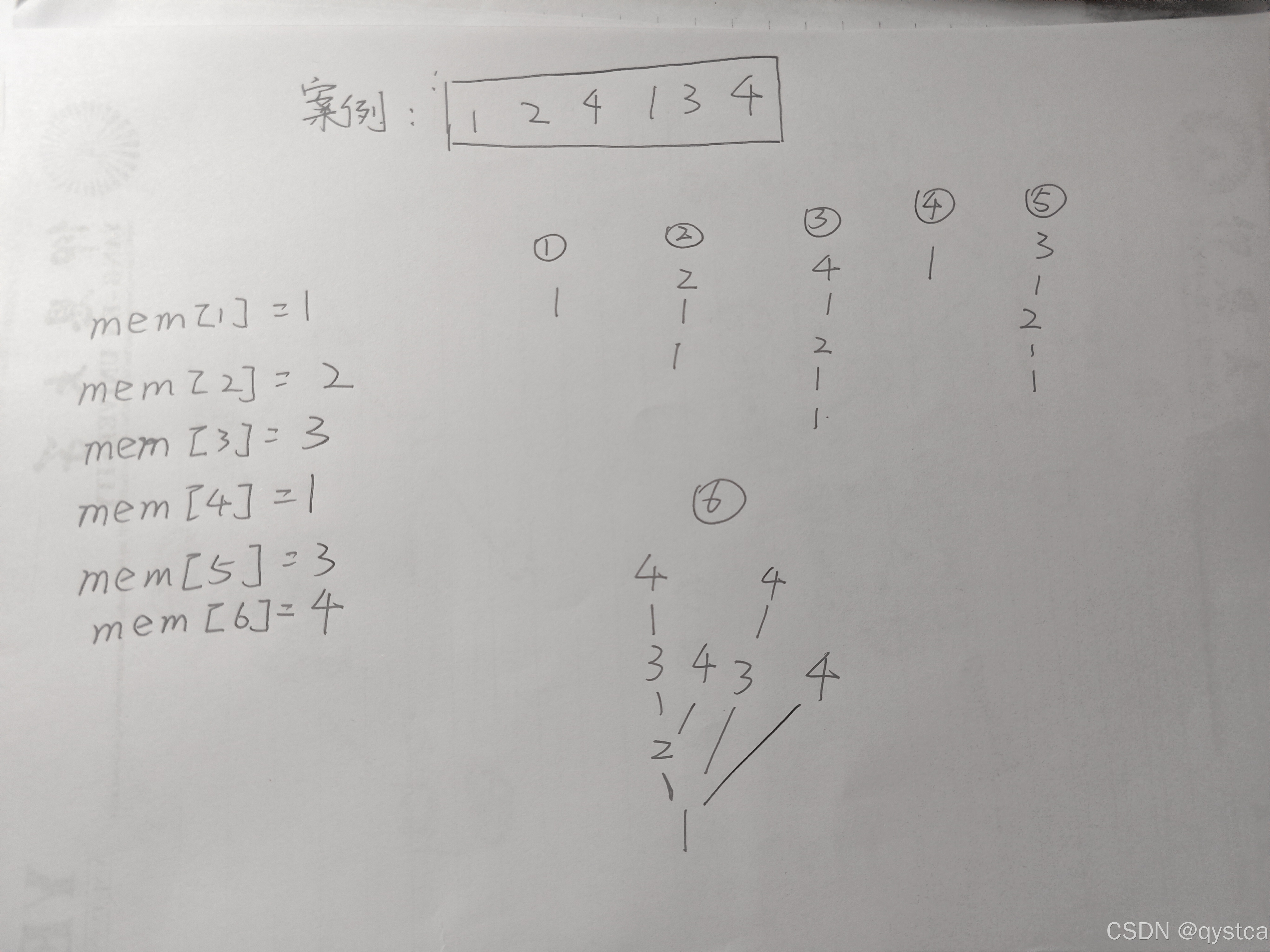
思路就是,求出第(1~n)为子序列结尾的最大长度,然后比较一下。用mem数组储存,我画了一个案例图,可以清楚地看出重复部分。
#include<iostream>
#include<algorithm>
using namespace std;
int n;
int nums[5005];
int mem[5005];
int dfs(int k)
{
if(mem[k])
return mem[k];
int sum = 1;
for(int i = 1 ; i < k ; i++)
{
if(nums[i] < nums[k])
sum = max(sum,dfs(i)+1);
}
mem[k] = sum;
return sum;
}
int main(void)
{
int ans = -1e10;
cin >> n;
for(int i = 1 ; i <= n ; i++)
cin >> nums[i];
for(int i = 1 ; i <= n ; i++)
{
ans = max(ans,dfs(i));
}
cout << ans;
return 0;
} 
动态规划:'正序'dp
#include<iostream>
#include<algorithm>
using namespace std;
int n;
int nums[5005];
int f[5005];
int main(void)
{
int ans;
cin >> n;
for(int i = 1 ; i <= n ; i++)
cin >> nums[i];
for(int i = 1 ; i <= n ; i++)
{
f[i] = 1;
for(int j = 1 ; j < i ; j++)
{
if(nums[j] < nums[i])
f[i] = max(f[i],f[j] + 1);
}
}
sort(f+1,f+1+n);
ans = f[n];
cout << ans;
return 0;
}